Bayesian Perspective on Memorization and Reconstruction

We introduce a new Bayesian perspective on the concept of data reconstruction, and leverage this viewpoint to propose a new security definition that, in certain settings, provably prevents reconstruction attacks. We use our paradigm to shed new light on one of the most notorious attacks in the privacy and memorization literature - fingerprinting code attacks (FPC). We argue that these attacks are really a form of membership inference attacks, rather than reconstruction attacks. Furthermore, we show that if the goal is solely to prevent reconstruction (but not membership inference), then in some cases the impossibility results derived from FPC no longer apply.

Nearly Optimal Sample Complexity for Learning with Label Proportions

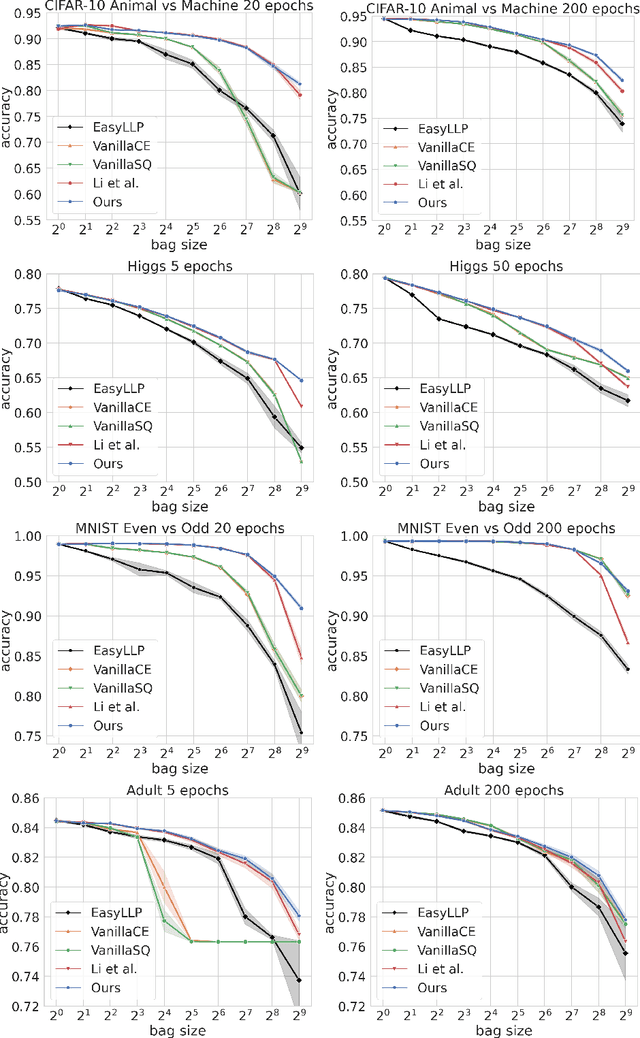
We investigate Learning from Label Proportions (LLP), a partial information setting where examples in a training set are grouped into bags, and only aggregate label values in each bag are available. Despite the partial observability, the goal is still to achieve small regret at the level of individual examples. We give results on the sample complexity of LLP under square loss, showing that our sample complexity is essentially optimal. From an algorithmic viewpoint, we rely on carefully designed variants of Empirical Risk Minimization, and Stochastic Gradient Descent algorithms, combined with ad hoc variance reduction techniques. On one hand, our theoretical results improve in important ways on the existing literature on LLP, specifically in the way the sample complexity depends on the bag size. On the other hand, we validate our algorithmic solutions on several datasets, demonstrating improved empirical performance (better accuracy for less samples) against recent baselines.

Lower Bounds for Differential Privacy Under Continual Observation and Online Threshold Queries

One of the most basic problems for studying the "price of privacy over time" is the so called private counter problem, introduced by Dwork et al. (2010) and Chan et al. (2010). In this problem, we aim to track the number of events that occur over time, while hiding the existence of every single event. More specifically, in every time step $t\in[T]$ we learn (in an online fashion) that $\Delta_t\geq 0$ new events have occurred, and must respond with an estimate $n_t\approx\sum_{j=1}^t \Delta_j$. The privacy requirement is that all of the outputs together, across all time steps, satisfy event level differential privacy. The main question here is how our error needs to depend on the total number of time steps $T$ and the total number of events $n$. Dwork et al. (2015) showed an upper bound of $O\left(\log(T)+\log^2(n)\right)$, and Henzinger et al. (2023) showed a lower bound of $\Omega\left(\min\{\log n, \log T\}\right)$. We show a new lower bound of $\Omega\left(\min\{n,\log T\}\right)$, which is tight w.r.t. the dependence on $T$, and is tight in the sparse case where $\log^2 n=O(\log T)$. Our lower bound has the following implications: $\bullet$ We show that our lower bound extends to the "online thresholds problem", where the goal is to privately answer many "quantile queries" when these queries are presented one-by-one. This resolves an open question of Bun et al. (2017). $\bullet$ Our lower bound implies, for the first time, a separation between the number of mistakes obtainable by a private online learner and a non-private online learner. This partially resolves a COLT'22 open question published by Sanyal and Ramponi. $\bullet$ Our lower bound also yields the first separation between the standard model of private online learning and a recently proposed relaxed variant of it, called private online prediction.

Private Truly-Everlasting Robust-Prediction

Private Everlasting Prediction (PEP), recently introduced by Naor et al. [2023], is a model for differentially private learning in which the learner never publicly releases a hypothesis. Instead, it provides black-box access to a "prediction oracle" that can predict the labels of an endless stream of unlabeled examples drawn from the underlying distribution. Importantly, PEP provides privacy both for the initial training set and for the endless stream of classification queries. We present two conceptual modifications to the definition of PEP, as well as new constructions exhibiting significant improvements over prior work. Specifically, (1) Robustness: PEP only guarantees accuracy provided that all the classification queries are drawn from the correct underlying distribution. A few out-of-distribution queries might break the validity of the prediction oracle for future queries, even for future queries which are sampled from the correct distribution. We incorporate robustness against such poisoning attacks into the definition of PEP, and show how to obtain it. (2) Dependence of the privacy parameter $\delta$ in the time horizon: We present a relaxed privacy definition, suitable for PEP, that allows us to disconnect the privacy parameter $\delta$ from the number of total time steps $T$. This allows us to obtain algorithms for PEP whose sample complexity is independent from $T$, thereby making them "truly everlasting". This is in contrast to prior work where the sample complexity grows with $polylog(T)$. (3) New constructions: Prior constructions for PEP exhibit sample complexity that is quadratic in the VC dimension of the target class. We present new constructions of PEP for axis-aligned rectangles and for decision-stumps that exhibit sample complexity linear in the dimension (instead of quadratic). We show that our constructions satisfy very strong robustness properties.

Hot PATE: Private Aggregation of Distributions for Diverse Task

The Private Aggregation of Teacher Ensembles (PATE) framework~\cite{PapernotAEGT:ICLR2017} is a versatile approach to privacy-preserving machine learning. In PATE, teacher models are trained on distinct portions of sensitive data, and their predictions are privately aggregated to label new training examples for a student model. Until now, PATE has primarily been explored with classification-like tasks, where each example possesses a ground-truth label, and knowledge is transferred to the student by labeling public examples. Generative AI models, however, excel in open ended \emph{diverse} tasks with multiple valid responses and scenarios that may not align with traditional labeled examples. Furthermore, the knowledge of models is often encapsulated in the response distribution itself and may be transferred from teachers to student in a more fluid way. We propose \emph{hot PATE}, tailored for the diverse setting. In hot PATE, each teacher model produces a response distribution and the aggregation method must preserve both privacy and diversity of responses. We demonstrate, analytically and empirically, that hot PATE achieves privacy-utility tradeoffs that are comparable to, and in diverse settings, significantly surpass, the baseline ``cold'' PATE.

Adaptive Data Analysis in a Balanced Adversarial Model

In adaptive data analysis, a mechanism gets $n$ i.i.d. samples from an unknown distribution $D$, and is required to provide accurate estimations to a sequence of adaptively chosen statistical queries with respect to $D$. Hardt and Ullman (FOCS 2014) and Steinke and Ullman (COLT 2015) showed that in general, it is computationally hard to answer more than $\Theta(n^2)$ adaptive queries, assuming the existence of one-way functions. However, these negative results strongly rely on an adversarial model that significantly advantages the adversarial analyst over the mechanism, as the analyst, who chooses the adaptive queries, also chooses the underlying distribution $D$. This imbalance raises questions with respect to the applicability of the obtained hardness results -- an analyst who has complete knowledge of the underlying distribution $D$ would have little need, if at all, to issue statistical queries to a mechanism which only holds a finite number of samples from $D$. We consider more restricted adversaries, called \emph{balanced}, where each such adversary consists of two separated algorithms: The \emph{sampler} who is the entity that chooses the distribution and provides the samples to the mechanism, and the \emph{analyst} who chooses the adaptive queries, but does not have a prior knowledge of the underlying distribution. We improve the quality of previous lower bounds by revisiting them using an efficient \emph{balanced} adversary, under standard public-key cryptography assumptions. We show that these stronger hardness assumptions are unavoidable in the sense that any computationally bounded \emph{balanced} adversary that has the structure of all known attacks, implies the existence of public-key cryptography.

Private Everlasting Prediction

A private learner is trained on a sample of labeled points and generates a hypothesis that can be used for predicting the labels of newly sampled points while protecting the privacy of the training set [Kasiviswannathan et al., FOCS 2008]. Research uncovered that private learners may need to exhibit significantly higher sample complexity than non-private learners as is the case with, e.g., learning of one-dimensional threshold functions [Bun et al., FOCS 2015, Alon et al., STOC 2019]. We explore prediction as an alternative to learning. Instead of putting forward a hypothesis, a predictor answers a stream of classification queries. Earlier work has considered a private prediction model with just a single classification query [Dwork and Feldman, COLT 2018]. We observe that when answering a stream of queries, a predictor must modify the hypothesis it uses over time, and, furthermore, that it must use the queries for this modification, hence introducing potential privacy risks with respect to the queries themselves. We introduce private everlasting prediction taking into account the privacy of both the training set and the (adaptively chosen) queries made to the predictor. We then present a generic construction of private everlasting predictors in the PAC model. The sample complexity of the initial training sample in our construction is quadratic (up to polylog factors) in the VC dimension of the concept class. Our construction allows prediction for all concept classes with finite VC dimension, and in particular threshold functions with constant size initial training sample, even when considered over infinite domains, whereas it is known that the sample complexity of privately learning threshold functions must grow as a function of the domain size and hence is impossible for infinite domains.

On Differentially Private Online Predictions

In this work we introduce an interactive variant of joint differential privacy towards handling online processes in which existing privacy definitions seem too restrictive. We study basic properties of this definition and demonstrate that it satisfies (suitable variants) of group privacy, composition, and post processing. We then study the cost of interactive joint privacy in the basic setting of online classification. We show that any (possibly non-private) learning rule can be effectively transformed to a private learning rule with only a polynomial overhead in the mistake bound. This demonstrates a stark difference with more restrictive notions of privacy such as the one studied by Golowich and Livni (2021), where only a double exponential overhead on the mistake bound is known (via an information theoretic upper bound).

On Differential Privacy and Adaptive Data Analysis with Bounded Space

We study the space complexity of the two related fields of differential privacy and adaptive data analysis. Specifically, (1) Under standard cryptographic assumptions, we show that there exists a problem P that requires exponentially more space to be solved efficiently with differential privacy, compared to the space needed without privacy. To the best of our knowledge, this is the first separation between the space complexity of private and non-private algorithms. (2) The line of work on adaptive data analysis focuses on understanding the number of samples needed for answering a sequence of adaptive queries. We revisit previous lower bounds at a foundational level, and show that they are a consequence of a space bottleneck rather than a sampling bottleneck. To obtain our results, we define and construct an encryption scheme with multiple keys that is built to withstand a limited amount of key leakage in a very particular way.

Concurrent Shuffle Differential Privacy Under Continual Observation

We introduce the concurrent shuffle model of differential privacy. In this model we have multiple concurrent shufflers permuting messages from different, possibly overlapping, batches of users. Similarly to the standard (single) shuffle model, the privacy requirement is that the concatenation of all shuffled messages should be differentially private. We study the private continual summation problem (a.k.a. the counter problem) and show that the concurrent shuffle model allows for significantly improved error compared to a standard (single) shuffle model. Specifically, we give a summation algorithm with error $\tilde{O}(n^{1/(2k+1)})$ with $k$ concurrent shufflers on a sequence of length $n$. Furthermore, we prove that this bound is tight for any $k$, even if the algorithm can choose the sizes of the batches adaptively. For $k=\log n$ shufflers, the resulting error is polylogarithmic, much better than $\tilde{\Theta}(n^{1/3})$ which we show is the smallest possible with a single shuffler. We use our online summation algorithm to get algorithms with improved regret bounds for the contextual linear bandit problem. In particular we get optimal $\tilde{O}(\sqrt{n})$ regret with $k= \tilde{\Omega}(\log n)$ concurrent shufflers.