Fingerprinting Codes Meet Geometry: Improved Lower Bounds for Private Query Release and Adaptive Data Analysis

Fingerprinting codes are a crucial tool for proving lower bounds in differential privacy. They have been used to prove tight lower bounds for several fundamental questions, especially in the ``low accuracy'' regime. Unlike reconstruction/discrepancy approaches however, they are more suited for query sets that arise naturally from the fingerprinting codes construction. In this work, we propose a general framework for proving fingerprinting type lower bounds, that allows us to tailor the technique to the geometry of the query set. Our approach allows us to prove several new results, including the following. First, we show that any (sample- and population-)accurate algorithm for answering $Q$ arbitrary adaptive counting queries over a universe $\mathcal{X}$ to accuracy $\alpha$ needs $\Omega(\frac{\sqrt{\log |\mathcal{X}|}\cdot \log Q}{\alpha^3})$ samples, matching known upper bounds. This shows that the approaches based on differential privacy are optimal for this question, and improves significantly on the previously known lower bounds of $\frac{\log Q}{\alpha^2}$ and $\min(\sqrt{Q}, \sqrt{\log |\mathcal{X}|})/\alpha^2$. Second, we show that any $(\varepsilon,\delta)$-DP algorithm for answering $Q$ counting queries to accuracy $\alpha$ needs $\Omega(\frac{\sqrt{ \log|\mathcal{X}| \log(1/\delta)} \log Q}{\varepsilon\alpha^2})$ samples, matching known upper bounds up to constants. Our framework allows for proving this bound via a direct correlation analysis and improves the prior bound of [BUV'14] by $\sqrt{\log(1/\delta)}$. Third, we characterize the sample complexity of answering a set of random $0$-$1$ queries under approximate differential privacy. We give new upper and lower bounds in different regimes. By combining them with known results, we can complete the whole picture.

DiM-Gestor: Co-Speech Gesture Generation with Adaptive Layer Normalization Mamba-2

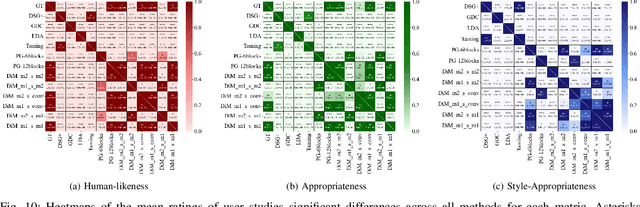
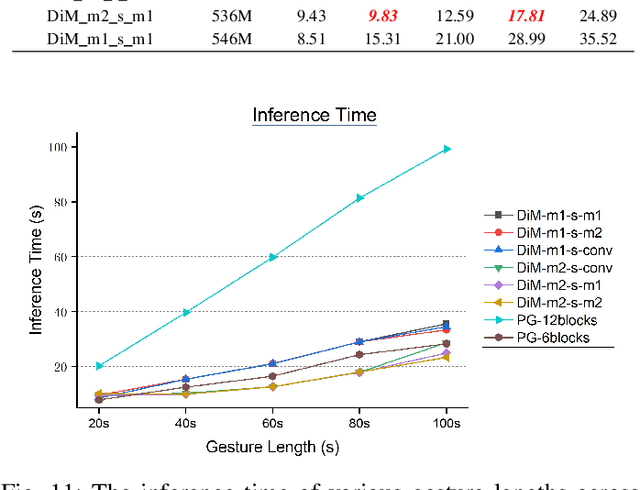
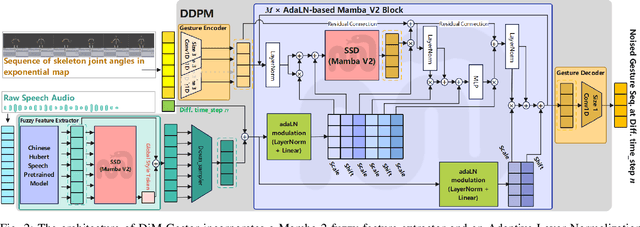
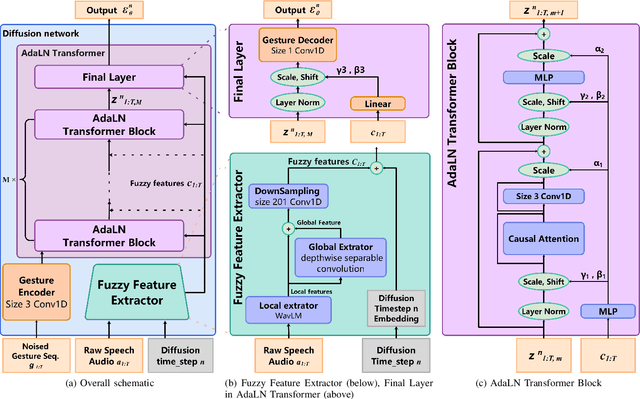
Speech-driven gesture generation using transformer-based generative models represents a rapidly advancing area within virtual human creation. However, existing models face significant challenges due to their quadratic time and space complexities, limiting scalability and efficiency. To address these limitations, we introduce DiM-Gestor, an innovative end-to-end generative model leveraging the Mamba-2 architecture. DiM-Gestor features a dual-component framework: (1) a fuzzy feature extractor and (2) a speech-to-gesture mapping module, both built on the Mamba-2. The fuzzy feature extractor, integrated with a Chinese Pre-trained Model and Mamba-2, autonomously extracts implicit, continuous speech features. These features are synthesized into a unified latent representation and then processed by the speech-to-gesture mapping module. This module employs an Adaptive Layer Normalization (AdaLN)-enhanced Mamba-2 mechanism to uniformly apply transformations across all sequence tokens. This enables precise modeling of the nuanced interplay between speech features and gesture dynamics. We utilize a diffusion model to train and infer diverse gesture outputs. Extensive subjective and objective evaluations conducted on the newly released Chinese Co-Speech Gestures dataset corroborate the efficacy of our proposed model. Compared with Transformer-based architecture, the assessments reveal that our approach delivers competitive results and significantly reduces memory usage, approximately 2.4 times, and enhances inference speeds by 2 to 4 times. Additionally, we released the CCG dataset, a Chinese Co-Speech Gestures dataset, comprising 15.97 hours (six styles across five scenarios) of 3D full-body skeleton gesture motion performed by professional Chinese TV broadcasters.

Speech-driven Personalized Gesture Synthetics: Harnessing Automatic Fuzzy Feature Inference

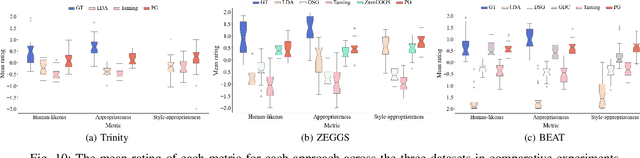
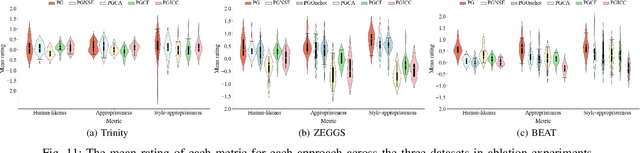
Speech-driven gesture generation is an emerging field within virtual human creation. However, a significant challenge lies in accurately determining and processing the multitude of input features (such as acoustic, semantic, emotional, personality, and even subtle unknown features). Traditional approaches, reliant on various explicit feature inputs and complex multimodal processing, constrain the expressiveness of resulting gestures and limit their applicability. To address these challenges, we present Persona-Gestor, a novel end-to-end generative model designed to generate highly personalized 3D full-body gestures solely relying on raw speech audio. The model combines a fuzzy feature extractor and a non-autoregressive Adaptive Layer Normalization (AdaLN) transformer diffusion architecture. The fuzzy feature extractor harnesses a fuzzy inference strategy that automatically infers implicit, continuous fuzzy features. These fuzzy features, represented as a unified latent feature, are fed into the AdaLN transformer. The AdaLN transformer introduces a conditional mechanism that applies a uniform function across all tokens, thereby effectively modeling the correlation between the fuzzy features and the gesture sequence. This module ensures a high level of gesture-speech synchronization while preserving naturalness. Finally, we employ the diffusion model to train and infer various gestures. Extensive subjective and objective evaluations on the Trinity, ZEGGS, and BEAT datasets confirm our model's superior performance to the current state-of-the-art approaches. Persona-Gestor improves the system's usability and generalization capabilities, setting a new benchmark in speech-driven gesture synthesis and broadening the horizon for virtual human technology. Supplementary videos and code can be accessed at https://zf223669.github.io/Diffmotion-v2-website/

Lower Bounds for Differential Privacy Under Continual Observation and Online Threshold Queries

One of the most basic problems for studying the "price of privacy over time" is the so called private counter problem, introduced by Dwork et al. (2010) and Chan et al. (2010). In this problem, we aim to track the number of events that occur over time, while hiding the existence of every single event. More specifically, in every time step $t\in[T]$ we learn (in an online fashion) that $\Delta_t\geq 0$ new events have occurred, and must respond with an estimate $n_t\approx\sum_{j=1}^t \Delta_j$. The privacy requirement is that all of the outputs together, across all time steps, satisfy event level differential privacy. The main question here is how our error needs to depend on the total number of time steps $T$ and the total number of events $n$. Dwork et al. (2015) showed an upper bound of $O\left(\log(T)+\log^2(n)\right)$, and Henzinger et al. (2023) showed a lower bound of $\Omega\left(\min\{\log n, \log T\}\right)$. We show a new lower bound of $\Omega\left(\min\{n,\log T\}\right)$, which is tight w.r.t. the dependence on $T$, and is tight in the sparse case where $\log^2 n=O(\log T)$. Our lower bound has the following implications: $\bullet$ We show that our lower bound extends to the "online thresholds problem", where the goal is to privately answer many "quantile queries" when these queries are presented one-by-one. This resolves an open question of Bun et al. (2017). $\bullet$ Our lower bound implies, for the first time, a separation between the number of mistakes obtainable by a private online learner and a non-private online learner. This partially resolves a COLT'22 open question published by Sanyal and Ramponi. $\bullet$ Our lower bound also yields the first separation between the standard model of private online learning and a recently proposed relaxed variant of it, called private online prediction.

The Cost of Parallelizing Boosting

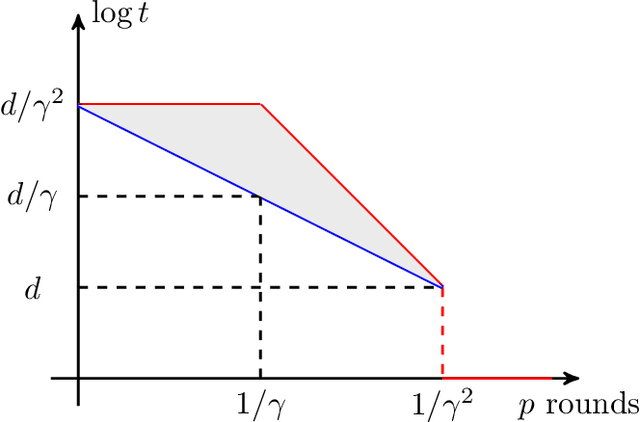
We study the cost of parallelizing weak-to-strong boosting algorithms for learning, following the recent work of Karbasi and Larsen. Our main results are two-fold: - First, we prove a tight lower bound, showing that even "slight" parallelization of boosting requires an exponential blow-up in the complexity of training. Specifically, let $\gamma$ be the weak learner's advantage over random guessing. The famous \textsc{AdaBoost} algorithm produces an accurate hypothesis by interacting with the weak learner for $\tilde{O}(1 / \gamma^2)$ rounds where each round runs in polynomial time. Karbasi and Larsen showed that "significant" parallelization must incur exponential blow-up: Any boosting algorithm either interacts with the weak learner for $\Omega(1 / \gamma)$ rounds or incurs an $\exp(d / \gamma)$ blow-up in the complexity of training, where $d$ is the VC dimension of the hypothesis class. We close the gap by showing that any boosting algorithm either has $\Omega(1 / \gamma^2)$ rounds of interaction or incurs a smaller exponential blow-up of $\exp(d)$. -Complementing our lower bound, we show that there exists a boosting algorithm using $\tilde{O}(1/(t \gamma^2))$ rounds, and only suffer a blow-up of $\exp(d \cdot t^2)$. Plugging in $t = \omega(1)$, this shows that the smaller blow-up in our lower bound is tight. More interestingly, this provides the first trade-off between the parallelism and the total work required for boosting.

Hot PATE: Private Aggregation of Distributions for Diverse Task

The Private Aggregation of Teacher Ensembles (PATE) framework~\cite{PapernotAEGT:ICLR2017} is a versatile approach to privacy-preserving machine learning. In PATE, teacher models are trained on distinct portions of sensitive data, and their predictions are privately aggregated to label new training examples for a student model. Until now, PATE has primarily been explored with classification-like tasks, where each example possesses a ground-truth label, and knowledge is transferred to the student by labeling public examples. Generative AI models, however, excel in open ended \emph{diverse} tasks with multiple valid responses and scenarios that may not align with traditional labeled examples. Furthermore, the knowledge of models is often encapsulated in the response distribution itself and may be transferred from teachers to student in a more fluid way. We propose \emph{hot PATE}, tailored for the diverse setting. In hot PATE, each teacher model produces a response distribution and the aggregation method must preserve both privacy and diversity of responses. We demonstrate, analytically and empirically, that hot PATE achieves privacy-utility tradeoffs that are comparable to, and in diverse settings, significantly surpass, the baseline ``cold'' PATE.

Tight Time-Space Lower Bounds for Constant-Pass Learning

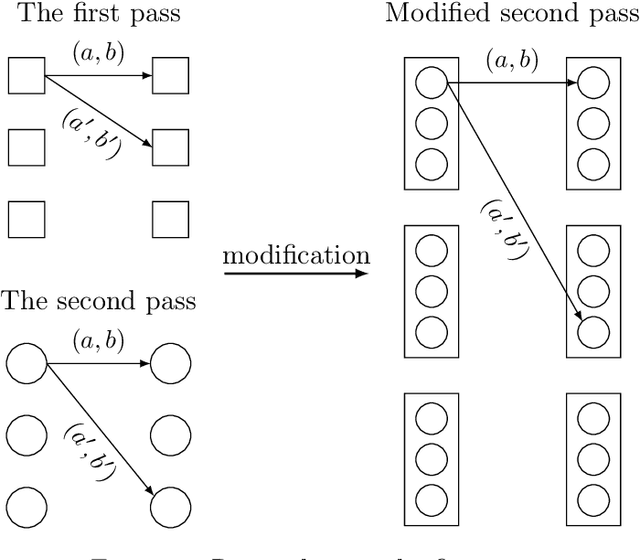
In his breakthrough paper, Raz showed that any parity learning algorithm requires either quadratic memory or an exponential number of samples [FOCS'16, JACM'19]. A line of work that followed extended this result to a large class of learning problems. Until recently, all these results considered learning in the streaming model, where each sample is drawn independently, and the learner is allowed a single pass over the stream of samples. Garg, Raz, and Tal [CCC'19] considered a stronger model, allowing multiple passes over the stream. In the $2$-pass model, they showed that learning parities of size $n$ requires either a memory of size $n^{1.5}$ or at least $2^{\sqrt{n}}$ samples. (Their result also generalizes to other learning problems.) In this work, for any constant $q$, we prove tight memory-sample lower bounds for any parity learning algorithm that makes $q$ passes over the stream of samples. We show that such a learner requires either $\Omega(n^{2})$ memory size or at least $2^{\Omega(n)}$ samples. Beyond establishing a tight lower bound, this is the first non-trivial lower bound for $q$-pass learning for any $q\ge 3$. Similar to prior work, our results extend to any learning problem with many nearly-orthogonal concepts. We complement the lower bound with an upper bound, showing that parity learning with $q$ passes can be done efficiently with $O(n^2/\log q)$ memory.

Õptimal Differentially Private Learning of Thresholds and Quasi-Concave Optimization

The problem of learning threshold functions is a fundamental one in machine learning. Classical learning theory implies sample complexity of $O(\xi^{-1} \log(1/\beta))$ (for generalization error $\xi$ with confidence $1-\beta$). The private version of the problem, however, is more challenging and in particular, the sample complexity must depend on the size $|X|$ of the domain. Progress on quantifying this dependence, via lower and upper bounds, was made in a line of works over the past decade. In this paper, we finally close the gap for approximate-DP and provide a nearly tight upper bound of $\tilde{O}(\log^* |X|)$, which matches a lower bound by Alon et al (that applies even with improper learning) and improves over a prior upper bound of $\tilde{O}((\log^* |X|)^{1.5})$ by Kaplan et al. We also provide matching upper and lower bounds of $\tilde{\Theta}(2^{\log^*|X|})$ for the additive error of private quasi-concave optimization (a related and more general problem). Our improvement is achieved via the novel Reorder-Slice-Compute paradigm for private data analysis which we believe will have further applications.

On the Robustness of CountSketch to Adaptive Inputs

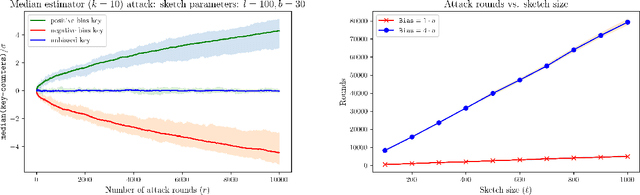
CountSketch is a popular dimensionality reduction technique that maps vectors to a lower dimension using randomized linear measurements. The sketch supports recovering $\ell_2$-heavy hitters of a vector (entries with $v[i]^2 \geq \frac{1}{k}\|\boldsymbol{v}\|^2_2$). We study the robustness of the sketch in adaptive settings where input vectors may depend on the output from prior inputs. Adaptive settings arise in processes with feedback or with adversarial attacks. We show that the classic estimator is not robust, and can be attacked with a number of queries of the order of the sketch size. We propose a robust estimator (for a slightly modified sketch) that allows for quadratic number of queries in the sketch size, which is an improvement factor of $\sqrt{k}$ (for $k$ heavy hitters) over prior work.