On the Robustness of CountSketch to Adaptive Inputs
Paper and Code
Feb 28, 2022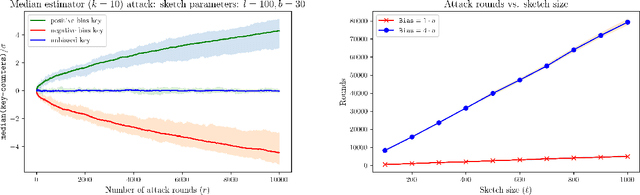
CountSketch is a popular dimensionality reduction technique that maps vectors to a lower dimension using randomized linear measurements. The sketch supports recovering $\ell_2$-heavy hitters of a vector (entries with $v[i]^2 \geq \frac{1}{k}\|\boldsymbol{v}\|^2_2$). We study the robustness of the sketch in adaptive settings where input vectors may depend on the output from prior inputs. Adaptive settings arise in processes with feedback or with adversarial attacks. We show that the classic estimator is not robust, and can be attacked with a number of queries of the order of the sketch size. We propose a robust estimator (for a slightly modified sketch) that allows for quadratic number of queries in the sketch size, which is an improvement factor of $\sqrt{k}$ (for $k$ heavy hitters) over prior work.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge