The Cost of Parallelizing Boosting
Paper and Code
Feb 23, 2024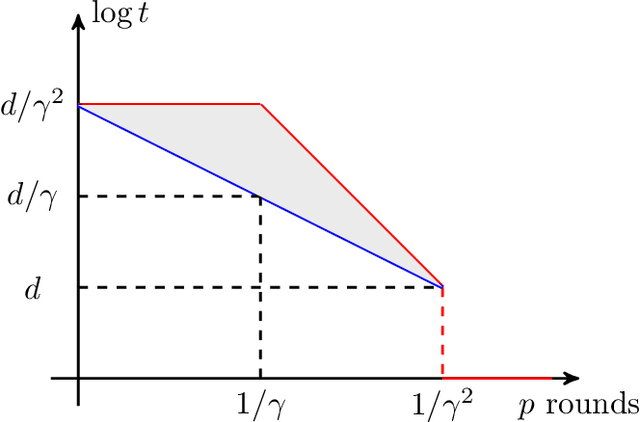
We study the cost of parallelizing weak-to-strong boosting algorithms for learning, following the recent work of Karbasi and Larsen. Our main results are two-fold: - First, we prove a tight lower bound, showing that even "slight" parallelization of boosting requires an exponential blow-up in the complexity of training. Specifically, let $\gamma$ be the weak learner's advantage over random guessing. The famous \textsc{AdaBoost} algorithm produces an accurate hypothesis by interacting with the weak learner for $\tilde{O}(1 / \gamma^2)$ rounds where each round runs in polynomial time. Karbasi and Larsen showed that "significant" parallelization must incur exponential blow-up: Any boosting algorithm either interacts with the weak learner for $\Omega(1 / \gamma)$ rounds or incurs an $\exp(d / \gamma)$ blow-up in the complexity of training, where $d$ is the VC dimension of the hypothesis class. We close the gap by showing that any boosting algorithm either has $\Omega(1 / \gamma^2)$ rounds of interaction or incurs a smaller exponential blow-up of $\exp(d)$. -Complementing our lower bound, we show that there exists a boosting algorithm using $\tilde{O}(1/(t \gamma^2))$ rounds, and only suffer a blow-up of $\exp(d \cdot t^2)$. Plugging in $t = \omega(1)$, this shows that the smaller blow-up in our lower bound is tight. More interestingly, this provides the first trade-off between the parallelism and the total work required for boosting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge