Junzhao Yang
The Cost of Parallelizing Boosting
Feb 23, 2024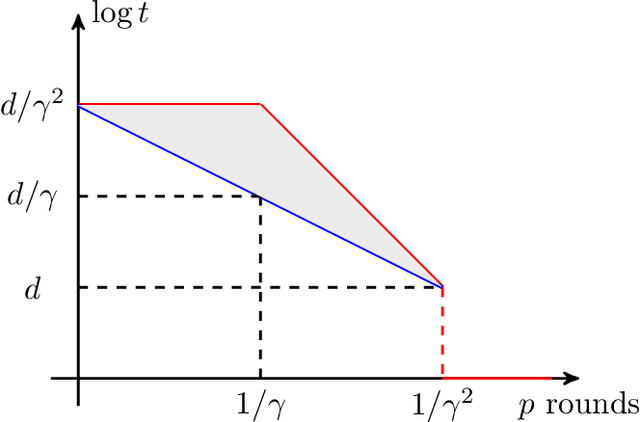
Abstract:We study the cost of parallelizing weak-to-strong boosting algorithms for learning, following the recent work of Karbasi and Larsen. Our main results are two-fold: - First, we prove a tight lower bound, showing that even "slight" parallelization of boosting requires an exponential blow-up in the complexity of training. Specifically, let $\gamma$ be the weak learner's advantage over random guessing. The famous \textsc{AdaBoost} algorithm produces an accurate hypothesis by interacting with the weak learner for $\tilde{O}(1 / \gamma^2)$ rounds where each round runs in polynomial time. Karbasi and Larsen showed that "significant" parallelization must incur exponential blow-up: Any boosting algorithm either interacts with the weak learner for $\Omega(1 / \gamma)$ rounds or incurs an $\exp(d / \gamma)$ blow-up in the complexity of training, where $d$ is the VC dimension of the hypothesis class. We close the gap by showing that any boosting algorithm either has $\Omega(1 / \gamma^2)$ rounds of interaction or incurs a smaller exponential blow-up of $\exp(d)$. -Complementing our lower bound, we show that there exists a boosting algorithm using $\tilde{O}(1/(t \gamma^2))$ rounds, and only suffer a blow-up of $\exp(d \cdot t^2)$. Plugging in $t = \omega(1)$, this shows that the smaller blow-up in our lower bound is tight. More interestingly, this provides the first trade-off between the parallelism and the total work required for boosting.
Tight Time-Space Lower Bounds for Constant-Pass Learning
Oct 12, 2023


Abstract:In his breakthrough paper, Raz showed that any parity learning algorithm requires either quadratic memory or an exponential number of samples [FOCS'16, JACM'19]. A line of work that followed extended this result to a large class of learning problems. Until recently, all these results considered learning in the streaming model, where each sample is drawn independently, and the learner is allowed a single pass over the stream of samples. Garg, Raz, and Tal [CCC'19] considered a stronger model, allowing multiple passes over the stream. In the $2$-pass model, they showed that learning parities of size $n$ requires either a memory of size $n^{1.5}$ or at least $2^{\sqrt{n}}$ samples. (Their result also generalizes to other learning problems.) In this work, for any constant $q$, we prove tight memory-sample lower bounds for any parity learning algorithm that makes $q$ passes over the stream of samples. We show that such a learner requires either $\Omega(n^{2})$ memory size or at least $2^{\Omega(n)}$ samples. Beyond establishing a tight lower bound, this is the first non-trivial lower bound for $q$-pass learning for any $q\ge 3$. Similar to prior work, our results extend to any learning problem with many nearly-orthogonal concepts. We complement the lower bound with an upper bound, showing that parity learning with $q$ passes can be done efficiently with $O(n^2/\log q)$ memory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge