David P. Woodruff
Carnegie Mellon University
Accelerating Scientific Research with Gemini: Case Studies and Common Techniques
Feb 03, 2026Abstract:Recent advances in large language models (LLMs) have opened new avenues for accelerating scientific research. While models are increasingly capable of assisting with routine tasks, their ability to contribute to novel, expert-level mathematical discovery is less understood. We present a collection of case studies demonstrating how researchers have successfully collaborated with advanced AI models, specifically Google's Gemini-based models (in particular Gemini Deep Think and its advanced variants), to solve open problems, refute conjectures, and generate new proofs across diverse areas in theoretical computer science, as well as other areas such as economics, optimization, and physics. Based on these experiences, we extract common techniques for effective human-AI collaboration in theoretical research, such as iterative refinement, problem decomposition, and cross-disciplinary knowledge transfer. While the majority of our results stem from this interactive, conversational methodology, we also highlight specific instances that push beyond standard chat interfaces. These include deploying the model as a rigorous adversarial reviewer to detect subtle flaws in existing proofs, and embedding it within a "neuro-symbolic" loop that autonomously writes and executes code to verify complex derivations. Together, these examples highlight the potential of AI not just as a tool for automation, but as a versatile, genuine partner in the creative process of scientific discovery.
Online Learning with Limited Information in the Sliding Window Model
Jan 07, 2026Abstract:Motivated by recent work on the experts problem in the streaming model, we consider the experts problem in the sliding window model. The sliding window model is a well-studied model that captures applications such as traffic monitoring, epidemic tracking, and automated trading, where recent information is more valuable than older data. Formally, we have $n$ experts, $T$ days, the ability to query the predictions of $q$ experts on each day, a limited amount of memory, and should achieve the (near-)optimal regret $\sqrt{nW}\text{polylog}(nT)$ regret over any window of the last $W$ days. While it is impossible to achieve such regret with $1$ query, we show that with $2$ queries we can achieve such regret and with only $\text{polylog}(nT)$ bits of memory. Not only are our algorithms optimal for sliding windows, but we also show for every interval $\mathcal{I}$ of days that we achieve $\sqrt{n|\mathcal{I}|}\text{polylog}(nT)$ regret with $2$ queries and only $\text{polylog}(nT)$ bits of memory, providing an exponential improvement on the memory of previous interval regret algorithms. Building upon these techniques, we address the bandit problem in data streams, where $q=1$, achieving $n T^{2/3}\text{polylog}(T)$ regret with $\text{polylog}(nT)$ memory, which is the first sublinear regret in the streaming model in the bandit setting with polylogarithmic memory; this can be further improved to the optimal $\mathcal{O}(\sqrt{nT})$ regret if the best expert's losses are in a random order.
Query-Efficient Locally Private Hypothesis Selection via the Scheffe Graph
Sep 19, 2025Abstract:We propose an algorithm with improved query-complexity for the problem of hypothesis selection under local differential privacy constraints. Given a set of $k$ probability distributions $Q$, we describe an algorithm that satisfies local differential privacy, performs $\tilde{O}(k^{3/2})$ non-adaptive queries to individuals who each have samples from a probability distribution $p$, and outputs a probability distribution from the set $Q$ which is nearly the closest to $p$. Previous algorithms required either $\Omega(k^2)$ queries or many rounds of interactive queries. Technically, we introduce a new object we dub the Scheff\'e graph, which captures structure of the differences between distributions in $Q$, and may be of more broad interest for hypothesis selection tasks.
Guessing Efficiently for Constrained Subspace Approximation
Apr 29, 2025Abstract:In this paper we study constrained subspace approximation problem. Given a set of $n$ points $\{a_1,\ldots,a_n\}$ in $\mathbb{R}^d$, the goal of the {\em subspace approximation} problem is to find a $k$ dimensional subspace that best approximates the input points. More precisely, for a given $p\geq 1$, we aim to minimize the $p$th power of the $\ell_p$ norm of the error vector $(\|a_1-\bm{P}a_1\|,\ldots,\|a_n-\bm{P}a_n\|)$, where $\bm{P}$ denotes the projection matrix onto the subspace and the norms are Euclidean. In \emph{constrained} subspace approximation (CSA), we additionally have constraints on the projection matrix $\bm{P}$. In its most general form, we require $\bm{P}$ to belong to a given subset $\mathcal{S}$ that is described explicitly or implicitly. We introduce a general framework for constrained subspace approximation. Our approach, that we term coreset-guess-solve, yields either $(1+\varepsilon)$-multiplicative or $\varepsilon$-additive approximations for a variety of constraints. We show that it provides new algorithms for partition-constrained subspace approximation with applications to {\it fair} subspace approximation, $k$-means clustering, and projected non-negative matrix factorization, among others. Specifically, while we reconstruct the best known bounds for $k$-means clustering in Euclidean spaces, we improve the known results for the remainder of the problems.
Beyond Worst-Case Dimensionality Reduction for Sparse Vectors
Feb 27, 2025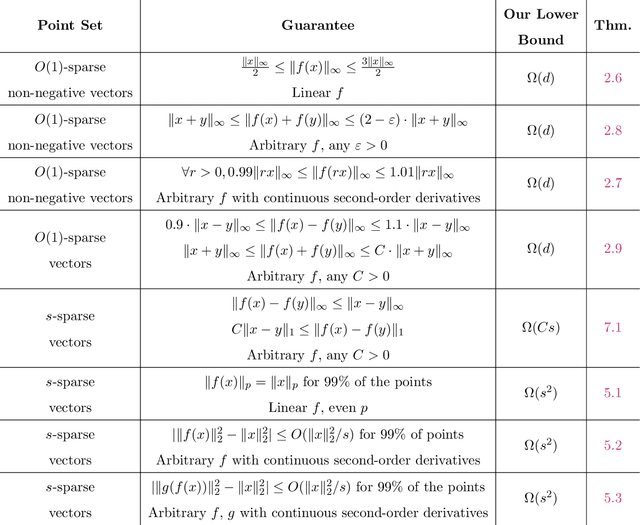
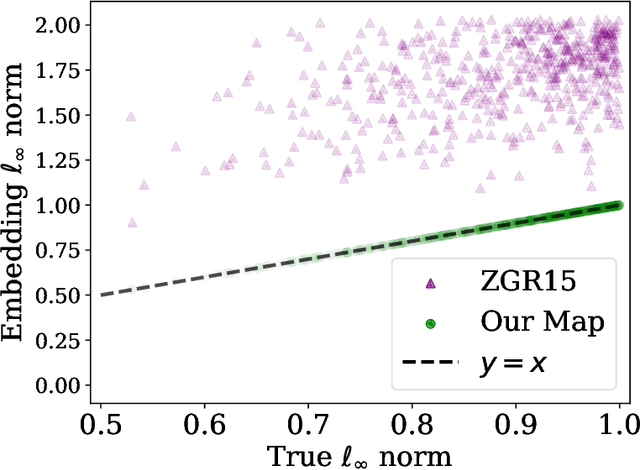
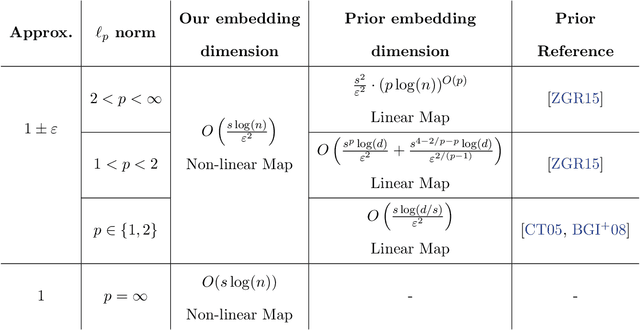
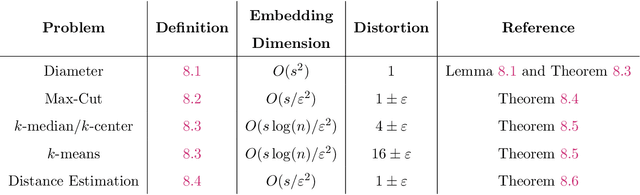
Abstract:We study beyond worst-case dimensionality reduction for $s$-sparse vectors. Our work is divided into two parts, each focusing on a different facet of beyond worst-case analysis: We first consider average-case guarantees. A folklore upper bound based on the birthday-paradox states: For any collection $X$ of $s$-sparse vectors in $\mathbb{R}^d$, there exists a linear map to $\mathbb{R}^{O(s^2)}$ which \emph{exactly} preserves the norm of $99\%$ of the vectors in $X$ in any $\ell_p$ norm (as opposed to the usual setting where guarantees hold for all vectors). We give lower bounds showing that this is indeed optimal in many settings: any oblivious linear map satisfying similar average-case guarantees must map to $\Omega(s^2)$ dimensions. The same lower bound also holds for a wide class of smooth maps, including `encoder-decoder schemes', where we compare the norm of the original vector to that of a smooth function of the embedding. These lower bounds reveal a separation result, as an upper bound of $O(s \log(d))$ is possible if we instead use arbitrary (possibly non-smooth) functions, e.g., via compressed sensing algorithms. Given these lower bounds, we specialize to sparse \emph{non-negative} vectors. For a dataset $X$ of non-negative $s$-sparse vectors and any $p \ge 1$, we can non-linearly embed $X$ to $O(s\log(|X|s)/\epsilon^2)$ dimensions while preserving all pairwise distances in $\ell_p$ norm up to $1\pm \epsilon$, with no dependence on $p$. Surprisingly, the non-negativity assumption enables much smaller embeddings than arbitrary sparse vectors, where the best known bounds suffer exponential dependence. Our map also guarantees \emph{exact} dimensionality reduction for $\ell_{\infty}$ by embedding into $O(s\log |X|)$ dimensions, which is tight. We show that both the non-linearity of $f$ and the non-negativity of $X$ are necessary, and provide downstream algorithmic improvements.
John Ellipsoids via Lazy Updates
Jan 03, 2025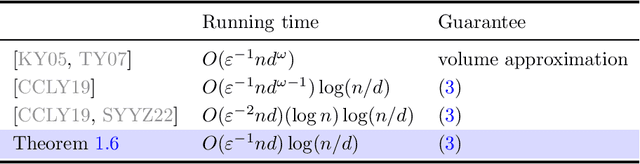
Abstract:We give a faster algorithm for computing an approximate John ellipsoid around $n$ points in $d$ dimensions. The best known prior algorithms are based on repeatedly computing the leverage scores of the points and reweighting them by these scores [CCLY19]. We show that this algorithm can be substantially sped up by delaying the computation of high accuracy leverage scores by using sampling, and then later computing multiple batches of high accuracy leverage scores via fast rectangular matrix multiplication. We also give low-space streaming algorithms for John ellipsoids using similar ideas.
On Socially Fair Low-Rank Approximation and Column Subset Selection
Dec 08, 2024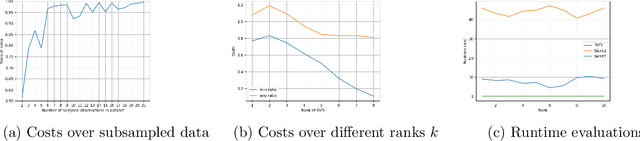
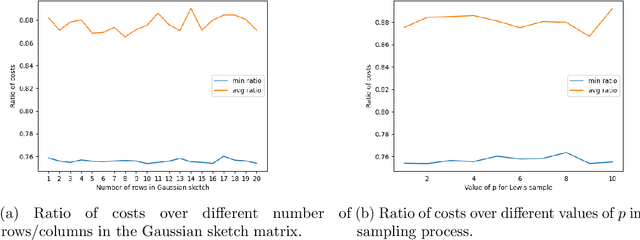
Abstract:Low-rank approximation and column subset selection are two fundamental and related problems that are applied across a wealth of machine learning applications. In this paper, we study the question of socially fair low-rank approximation and socially fair column subset selection, where the goal is to minimize the loss over all sub-populations of the data. We show that surprisingly, even constant-factor approximation to fair low-rank approximation requires exponential time under certain standard complexity hypotheses. On the positive side, we give an algorithm for fair low-rank approximation that, for a constant number of groups and constant-factor accuracy, runs in $2^{\text{poly}(k)}$ time rather than the na\"{i}ve $n^{\text{poly}(k)}$, which is a substantial improvement when the dataset has a large number $n$ of observations. We then show that there exist bicriteria approximation algorithms for fair low-rank approximation and fair column subset selection that run in polynomial time.
LevAttention: Time, Space, and Streaming Efficient Algorithm for Heavy Attentions
Oct 07, 2024Abstract:A central problem related to transformers can be stated as follows: given two $n \times d$ matrices $Q$ and $K$, and a non-negative function $f$, define the matrix $A$ as follows: (1) apply the function $f$ to each entry of the $n \times n$ matrix $Q K^T$, and then (2) normalize each of the row sums of $A$ to be equal to $1$. The matrix $A$ can be computed in $O(n^2 d)$ time assuming $f$ can be applied to a number in constant time, but the quadratic dependence on $n$ is prohibitive in applications where it corresponds to long context lengths. For a large class of functions $f$, we show how to find all the ``large attention scores", i.e., entries of $A$ which are at least a positive value $\varepsilon$, in time with linear dependence on $n$ (i.e., $n \cdot \textrm{poly}(d/\varepsilon)$) for a positive parameter $\varepsilon > 0$. Our class of functions include all functions $f$ of the form $f(x) = |x|^p$, as explored recently in transformer models. Using recently developed tools from randomized numerical linear algebra, we prove that for any $K$, there is a ``universal set" $U \subset [n]$ of size independent of $n$, such that for any $Q$ and any row $i$, the large attention scores $A_{i,j}$ in row $i$ of $A$ all have $j \in U$. We also find $U$ in $n \cdot \textrm{poly}(d/\varepsilon)$ time. Notably, we (1) make no assumptions on the data, (2) our workspace does not grow with $n$, and (3) our algorithms can be computed in streaming and parallel settings. We call the attention mechanism that uses only the subset of keys in the universal set as LevAttention since our algorithm to identify the universal set $U$ is based on leverage scores. We empirically show the benefits of our scheme for vision transformers, showing how to train new models that use our universal set while training as well, showing that our model is able to consistently select ``important keys'' during training.
Optimal Sketching for Residual Error Estimation for Matrix and Vector Norms
Aug 16, 2024
Abstract:We study the problem of residual error estimation for matrix and vector norms using a linear sketch. Such estimates can be used, for example, to quickly assess how useful a more expensive low-rank approximation computation will be. The matrix case concerns the Frobenius norm and the task is to approximate the $k$-residual $\|A - A_k\|_F$ of the input matrix $A$ within a $(1+\epsilon)$-factor, where $A_k$ is the optimal rank-$k$ approximation. We provide a tight bound of $\Theta(k^2/\epsilon^4)$ on the size of bilinear sketches, which have the form of a matrix product $SAT$. This improves the previous $O(k^2/\epsilon^6)$ upper bound in (Andoni et al. SODA 2013) and gives the first non-trivial lower bound, to the best of our knowledge. In our algorithm, our sketching matrices $S$ and $T$ can both be sparse matrices, allowing for a very fast update time. We demonstrate that this gives a substantial advantage empirically, for roughly the same sketch size and accuracy as in previous work. For the vector case, we consider the $\ell_p$-norm for $p>2$, where the task is to approximate the $k$-residual $\|x - x_k\|_p$ up to a constant factor, where $x_k$ is the optimal $k$-sparse approximation to $x$. Such vector norms are frequently studied in the data stream literature and are useful for finding frequent items or so-called heavy hitters. We establish an upper bound of $O(k^{2/p}n^{1-2/p}\operatorname{poly}(\log n))$ for constant $\epsilon$ on the dimension of a linear sketch for this problem. Our algorithm can be extended to the $\ell_p$ sparse recovery problem with the same sketching dimension, which seems to be the first such bound for $p > 2$. We also show an $\Omega(k^{2/p}n^{1-2/p})$ lower bound for the sparse recovery problem, which is tight up to a $\mathrm{poly}(\log n)$ factor.
Nearly Linear Sparsification of $\ell_p$ Subspace Approximation
Jul 03, 2024Abstract:The $\ell_p$ subspace approximation problem is an NP-hard low rank approximation problem that generalizes the median hyperplane problem ($p = 1$), principal component analysis ($p = 2$), and the center hyperplane problem ($p = \infty$). A popular approach to cope with the NP-hardness of this problem is to compute a strong coreset, which is a small weighted subset of the input points which simultaneously approximates the cost of every $k$-dimensional subspace, typically to $(1+\varepsilon)$ relative error for a small constant $\varepsilon$. We obtain the first algorithm for constructing a strong coreset for $\ell_p$ subspace approximation with a nearly optimal dependence on the rank parameter $k$, obtaining a nearly linear bound of $\tilde O(k)\mathrm{poly}(\varepsilon^{-1})$ for $p<2$ and $\tilde O(k^{p/2})\mathrm{poly}(\varepsilon^{-1})$ for $p>2$. Prior constructions either achieved a similar size bound but produced a coreset with a modification of the original points [SW18, FKW21], or produced a coreset of the original points but lost $\mathrm{poly}(k)$ factors in the coreset size [HV20, WY23]. Our techniques also lead to the first nearly optimal online strong coresets for $\ell_p$ subspace approximation with similar bounds as the offline setting, resolving a problem of [WY23]. All prior approaches lose $\mathrm{poly}(k)$ factors in this setting, even when allowed to modify the original points.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge