On Optimal Steering to Achieve Exact Fairness

To fix the 'bias in, bias out' problem in fair machine learning, it is important to steer feature distributions of data or internal representations of Large Language Models (LLMs) to ideal ones that guarantee group-fair outcomes. Previous work on fair generative models and representation steering could greatly benefit from provable fairness guarantees on the model output. We define a distribution as ideal if the minimizer of any cost-sensitive risk on it is guaranteed to have exact group-fair outcomes (e.g., demographic parity, equal opportunity)-in other words, it has no fairness-utility trade-off. We formulate an optimization program for optimal steering by finding the nearest ideal distribution in KL-divergence, and provide efficient algorithms for it when the underlying distributions come from well-known parametric families (e.g., normal, log-normal). Empirically, our optimal steering techniques on both synthetic and real-world datasets improve fairness without diminishing utility (and sometimes even improve utility). We demonstrate affine steering of LLM representations to reduce bias in multi-class classification, e.g., occupation prediction from a short biography in Bios dataset (De-Arteaga et al.). Furthermore, we steer internal representations of LLMs towards desired outputs so that it works equally well across different groups.

When Routers, Switches and Interconnects Compute: A processing-in-interconnect Paradigm for Scalable Neuromorphic AI

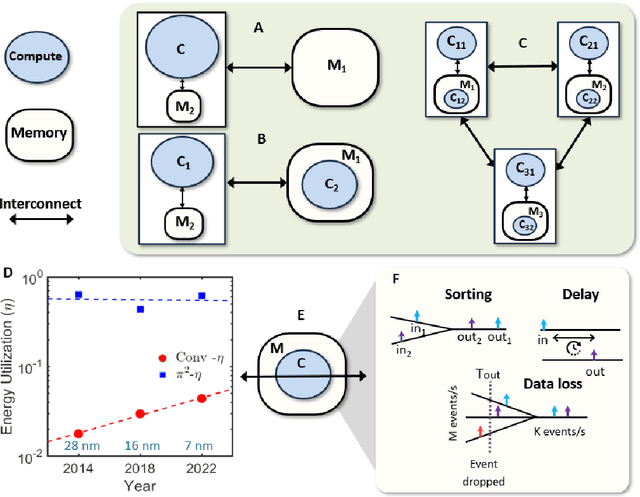
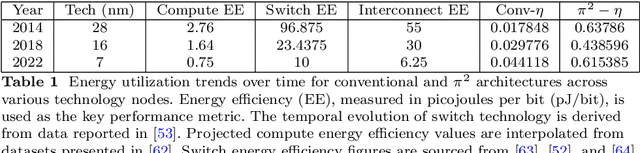
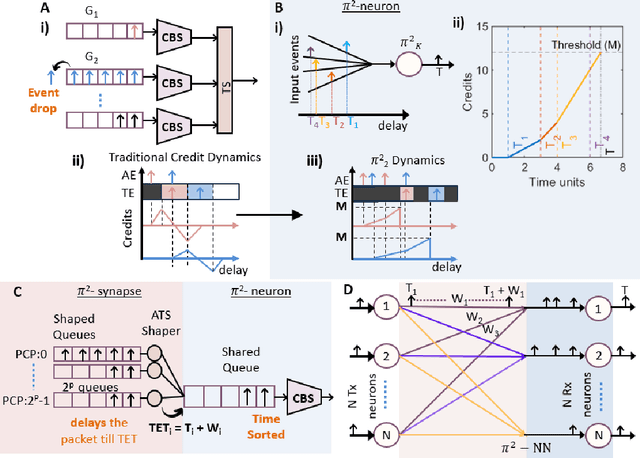
Routing, switching, and the interconnect fabric are essential for large-scale neuromorphic computing. While this fabric only plays a supporting role in the process of computing, for large AI workloads it ultimately determines energy consumption and speed. In this paper, we address this bottleneck by asking: (a) What computing paradigms are inherent in existing routing, switching, and interconnect systems, and how can they be used to implement a processing-in-Interconnect (\pi^2) computing paradigm? and (b) leveraging current and future interconnect trends, how will a \pi^2 system's performance scale compared to other neuromorphic architectures? For (a), we show that operations required for typical AI workloads can be mapped onto delays, causality, time-outs, packet drop, and broadcast operations -- primitives already implemented in packet-switching and packet-routing hardware. We show that existing buffering and traffic-shaping embedded algorithms can be leveraged to implement neuron models and synaptic operations. Additionally, a knowledge-distillation framework can train and cross-map well-established neural network topologies onto $\pi^2$ without degrading generalization performance. For (b), analytical modeling shows that, unlike other neuromorphic platforms, the energy scaling of $\pi^2$ improves with interconnect bandwidth and energy efficiency. We predict that by leveraging trends in interconnect technology, a \pi^2 architecture can be more easily scaled to execute brain-scale AI inference workloads with power consumption levels in the range of hundreds of watts.

DO-EM: Density Operator Expectation Maximization

Density operators, quantum generalizations of probability distributions, are gaining prominence in machine learning due to their foundational role in quantum computing. Generative modeling based on density operator models (\textbf{DOMs}) is an emerging field, but existing training algorithms -- such as those for the Quantum Boltzmann Machine -- do not scale to real-world data, such as the MNIST dataset. The Expectation-Maximization algorithm has played a fundamental role in enabling scalable training of probabilistic latent variable models on real-world datasets. \textit{In this paper, we develop an Expectation-Maximization framework to learn latent variable models defined through \textbf{DOMs} on classical hardware, with resources comparable to those used for probabilistic models, while scaling to real-world data.} However, designing such an algorithm is nontrivial due to the absence of a well-defined quantum analogue to conditional probability, which complicates the Expectation step. To overcome this, we reformulate the Expectation step as a quantum information projection (QIP) problem and show that the Petz Recovery Map provides a solution under sufficient conditions. Using this formulation, we introduce the Density Operator Expectation Maximization (DO-EM) algorithm -- an iterative Minorant-Maximization procedure that optimizes a quantum evidence lower bound. We show that the \textbf{DO-EM} algorithm ensures non-decreasing log-likelihood across iterations for a broad class of models. Finally, we present Quantum Interleaved Deep Boltzmann Machines (\textbf{QiDBMs}), a \textbf{DOM} that can be trained with the same resources as a DBM. When trained with \textbf{DO-EM} under Contrastive Divergence, a \textbf{QiDBM} outperforms larger classical DBMs in image generation on the MNIST dataset, achieving a 40--60\% reduction in the Fr\'echet Inception Distance.

LevAttention: Time, Space, and Streaming Efficient Algorithm for Heavy Attentions

A central problem related to transformers can be stated as follows: given two $n \times d$ matrices $Q$ and $K$, and a non-negative function $f$, define the matrix $A$ as follows: (1) apply the function $f$ to each entry of the $n \times n$ matrix $Q K^T$, and then (2) normalize each of the row sums of $A$ to be equal to $1$. The matrix $A$ can be computed in $O(n^2 d)$ time assuming $f$ can be applied to a number in constant time, but the quadratic dependence on $n$ is prohibitive in applications where it corresponds to long context lengths. For a large class of functions $f$, we show how to find all the ``large attention scores", i.e., entries of $A$ which are at least a positive value $\varepsilon$, in time with linear dependence on $n$ (i.e., $n \cdot \textrm{poly}(d/\varepsilon)$) for a positive parameter $\varepsilon > 0$. Our class of functions include all functions $f$ of the form $f(x) = |x|^p$, as explored recently in transformer models. Using recently developed tools from randomized numerical linear algebra, we prove that for any $K$, there is a ``universal set" $U \subset [n]$ of size independent of $n$, such that for any $Q$ and any row $i$, the large attention scores $A_{i,j}$ in row $i$ of $A$ all have $j \in U$. We also find $U$ in $n \cdot \textrm{poly}(d/\varepsilon)$ time. Notably, we (1) make no assumptions on the data, (2) our workspace does not grow with $n$, and (3) our algorithms can be computed in streaming and parallel settings. We call the attention mechanism that uses only the subset of keys in the universal set as LevAttention since our algorithm to identify the universal set $U$ is based on leverage scores. We empirically show the benefits of our scheme for vision transformers, showing how to train new models that use our universal set while training as well, showing that our model is able to consistently select ``important keys'' during training.

Predicting Ground State Properties: Constant Sample Complexity and Deep Learning Algorithms

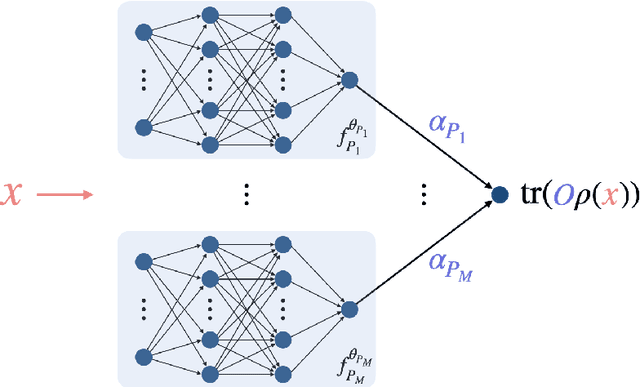
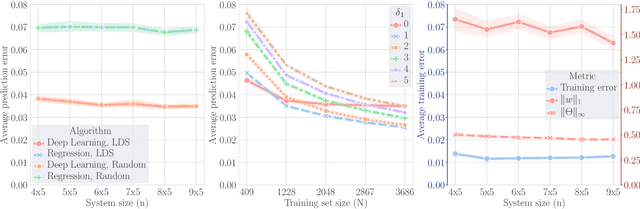
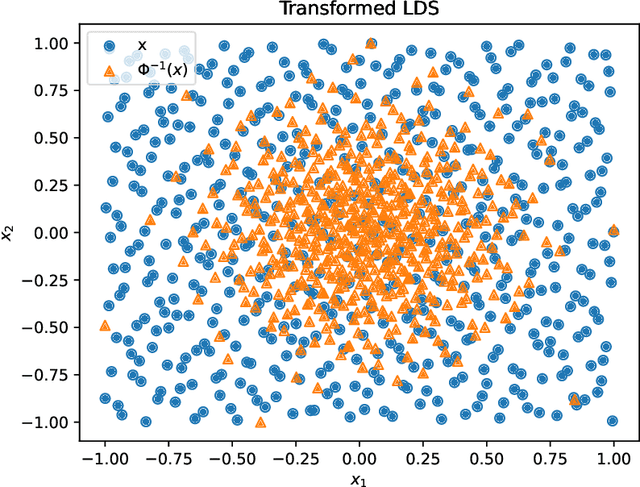
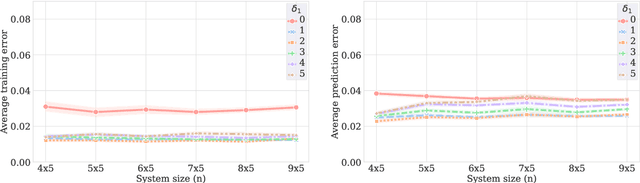
A fundamental problem in quantum many-body physics is that of finding ground states of local Hamiltonians. A number of recent works gave provably efficient machine learning (ML) algorithms for learning ground states. Specifically, [Huang et al. Science 2022], introduced an approach for learning properties of the ground state of an $n$-qubit gapped local Hamiltonian $H$ from only $n^{\mathcal{O}(1)}$ data points sampled from Hamiltonians in the same phase of matter. This was subsequently improved by [Lewis et al. Nature Communications 2024], to $\mathcal{O}(\log n)$ samples when the geometry of the $n$-qubit system is known. In this work, we introduce two approaches that achieve a constant sample complexity, independent of system size $n$, for learning ground state properties. Our first algorithm consists of a simple modification of the ML model used by Lewis et al. and applies to a property of interest known beforehand. Our second algorithm, which applies even if a description of the property is not known, is a deep neural network model. While empirical results showing the performance of neural networks have been demonstrated, to our knowledge, this is the first rigorous sample complexity bound on a neural network model for predicting ground state properties. We also perform numerical experiments that confirm the improved scaling of our approach compared to earlier results.

Random Separating Hyperplane Theorem and Learning Polytopes

The Separating Hyperplane theorem is a fundamental result in Convex Geometry with myriad applications. Our first result, Random Separating Hyperplane Theorem (RSH), is a strengthening of this for polytopes. $\rsh$ asserts that if the distance between $a$ and a polytope $K$ with $k$ vertices and unit diameter in $\Re^d$ is at least $\delta$, where $\delta$ is a fixed constant in $(0,1)$, then a randomly chosen hyperplane separates $a$ and $K$ with probability at least $1/poly(k)$ and margin at least $\Omega \left(\delta/\sqrt{d} \right)$. An immediate consequence of our result is the first near optimal bound on the error increase in the reduction from a Separation oracle to an Optimization oracle over a polytope. RSH has algorithmic applications in learning polytopes. We consider a fundamental problem, denoted the ``Hausdorff problem'', of learning a unit diameter polytope $K$ within Hausdorff distance $\delta$, given an optimization oracle for $K$. Using RSH, we show that with polynomially many random queries to the optimization oracle, $K$ can be approximated within error $O(\delta)$. To our knowledge this is the first provable algorithm for the Hausdorff Problem. Building on this result, we show that if the vertices of $K$ are well-separated, then an optimization oracle can be used to generate a list of points, each within Hausdorff distance $O(\delta)$ of $K$, with the property that the list contains a point close to each vertex of $K$. Further, we show how to prune this list to generate a (unique) approximation to each vertex of the polytope. We prove that in many latent variable settings, e.g., topic modeling, LDA, optimization oracles do exist provided we project to a suitable SVD subspace. Thus, our work yields the first efficient algorithm for finding approximations to the vertices of the latent polytope under the well-separatedness assumption.

BNSynth: Bounded Boolean Functional Synthesis

The automated synthesis of correct-by-construction Boolean functions from logical specifications is known as the Boolean Functional Synthesis (BFS) problem. BFS has many application areas that range from software engineering to circuit design. In this paper, we introduce a tool BNSynth, that is the first to solve the BFS problem under a given bound on the solution space. Bounding the solution space induces the synthesis of smaller functions that benefit resource constrained areas such as circuit design. BNSynth uses a counter-example guided, neural approach to solve the bounded BFS problem. Initial results show promise in synthesizing smaller solutions; we observe at least \textbf{3.2X} (and up to \textbf{24X}) improvement in the reduction of solution size on average, as compared to state of the art tools on our benchmarks. BNSynth is available on GitHub under an open source license.

Reliable quantum kernel classification using fewer circuit evaluations

Quantum kernel methods are a candidate for quantum speed-ups in supervised machine learning. The number of quantum measurements $N$ required for a reasonable kernel estimate is a critical resource, both from complexity considerations and because of the constraints of near-term quantum hardware. We emphasize that for classification tasks, the aim is accurate classification and not accurate kernel evaluation, and demonstrate that the former is more resource efficient. In general, the uncertainty in the quantum kernel, arising from finite sampling, leads to misclassifications over some kernel instantiations. We introduce a suitable performance metric that characterizes the robustness or reliability of classification over a dataset, and obtain a bound for $N$ which ensures, with high probability, that classification errors over a dataset are bounded by the margin errors of an idealized quantum kernel classifier. Using techniques of robust optimization, we then show that the number of quantum measurements can be significantly reduced by a robust formulation of the original support vector machine. We consider the SWAP test and the GATES test quantum circuits for kernel evaluations, and show that the SWAP test is always less reliable than the GATES test for any $N$. Our strategy is applicable to uncertainty in quantum kernels arising from {\em any} source of noise, although we only consider the statistical sampling noise in our analysis.

Rawlsian Fair Adaptation of Deep Learning Classifiers

Group-fairness in classification aims for equality of a predictive utility across different sensitive sub-populations, e.g., race or gender. Equality or near-equality constraints in group-fairness often worsen not only the aggregate utility but also the utility for the least advantaged sub-population. In this paper, we apply the principles of Pareto-efficiency and least-difference to the utility being accuracy, as an illustrative example, and arrive at the Rawls classifier that minimizes the error rate on the worst-off sensitive sub-population. Our mathematical characterization shows that the Rawls classifier uniformly applies a threshold to an ideal score of features, in the spirit of fair equality of opportunity. In practice, such a score or a feature representation is often computed by a black-box model that has been useful but unfair. Our second contribution is practical Rawlsian fair adaptation of any given black-box deep learning model, without changing the score or feature representation it computes. Given any score function or feature representation and only its second-order statistics on the sensitive sub-populations, we seek a threshold classifier on the given score or a linear threshold classifier on the given feature representation that achieves the Rawls error rate restricted to this hypothesis class. Our technical contribution is to formulate the above problems using ambiguous chance constraints, and to provide efficient algorithms for Rawlsian fair adaptation, along with provable upper bounds on the Rawls error rate. Our empirical results show significant improvement over state-of-the-art group-fair algorithms, even without retraining for fairness.

DSLR: Dynamic to Static LiDAR Scan Reconstruction Using Adversarially Trained Autoencoder

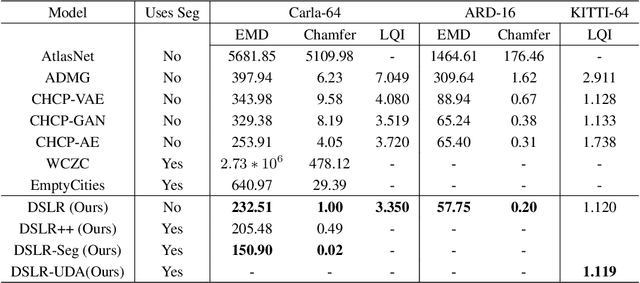
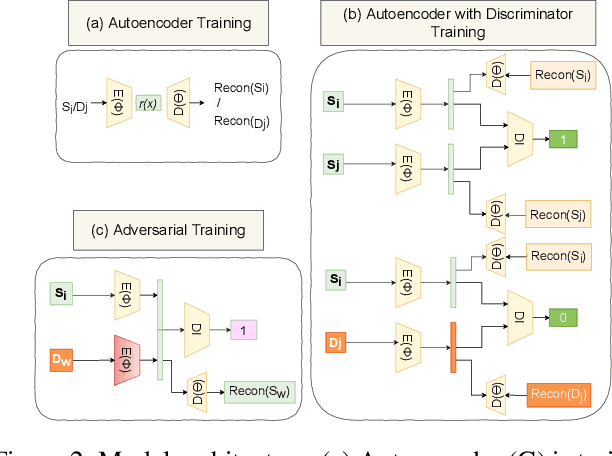
Accurate reconstruction of static environments from LiDAR scans of scenes containing dynamic objects, which we refer to as Dynamic to Static Translation (DST), is an important area of research in Autonomous Navigation. This problem has been recently explored for visual SLAM, but to the best of our knowledge no work has been attempted to address DST for LiDAR scans. The problem is of critical importance due to wide-spread adoption of LiDAR in Autonomous Vehicles. We show that state-of the art methods developed for the visual domain when adapted for LiDAR scans perform poorly. We develop DSLR, a deep generative model which learns a mapping between dynamic scan to its static counterpart through an adversarially trained autoencoder. Our model yields the first solution for DST on LiDAR that generates static scans without using explicit segmentation labels. DSLR cannot always be applied to real world data due to lack of paired dynamic-static scans. Using Unsupervised Domain Adaptation, we propose DSLR-UDA for transfer to real world data and experimentally show that this performs well in real world settings. Additionally, if segmentation information is available, we extend DSLR to DSLR-Seg to further improve the reconstruction quality. DSLR gives the state of the art performance on simulated and real-world datasets and also shows at least 4x improvement. We show that DSLR, unlike the existing baselines, is a practically viable model with its reconstruction quality within the tolerable limits for tasks pertaining to autonomous navigation like SLAM in dynamic environments.