Quantum advantage for learning shallow neural networks with natural data distributions

The application of quantum computers to machine learning tasks is an exciting potential direction to explore in search of quantum advantage. In the absence of large quantum computers to empirically evaluate performance, theoretical frameworks such as the quantum probably approximately correct (PAC) and quantum statistical query (QSQ) models have been proposed to study quantum algorithms for learning classical functions. Despite numerous works investigating quantum advantage in these models, we nevertheless only understand it at two extremes: either exponential quantum advantages for uniform input distributions or no advantage for potentially adversarial distributions. In this work, we study the gap between these two regimes by designing an efficient quantum algorithm for learning periodic neurons in the QSQ model over a broad range of non-uniform distributions, which includes Gaussian, generalized Gaussian, and logistic distributions. To our knowledge, our work is also the first result in quantum learning theory for classical functions that explicitly considers real-valued functions. Recent advances in classical learning theory prove that learning periodic neurons is hard for any classical gradient-based algorithm, giving us an exponential quantum advantage over such algorithms, which are the standard workhorses of machine learning. Moreover, in some parameter regimes, the problem remains hard for classical statistical query algorithms and even general classical algorithms learning under small amounts of noise.

Predicting adaptively chosen observables in quantum systems

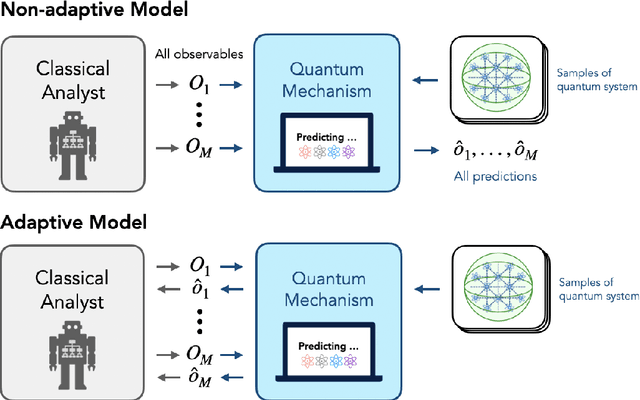
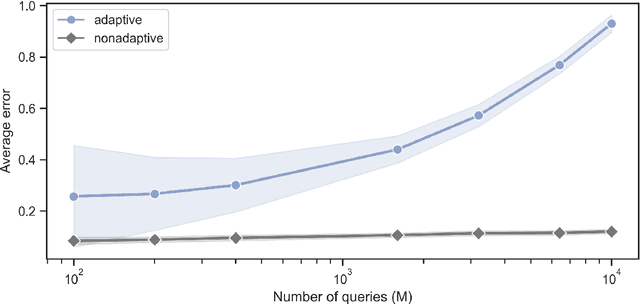
Recent advances have demonstrated that $\mathcal{O}(\log M)$ measurements suffice to predict $M$ properties of arbitrarily large quantum many-body systems. However, these remarkable findings assume that the properties to be predicted are chosen independently of the data. This assumption can be violated in practice, where scientists adaptively select properties after looking at previous predictions. This work investigates the adaptive setting for three classes of observables: local, Pauli, and bounded-Frobenius-norm observables. We prove that $\Omega(\sqrt{M})$ samples of an arbitrarily large unknown quantum state are necessary to predict expectation values of $M$ adaptively chosen local and Pauli observables. We also present computationally-efficient algorithms that achieve this information-theoretic lower bound. In contrast, for bounded-Frobenius-norm observables, we devise an algorithm requiring only $\mathcal{O}(\log M)$ samples, independent of system size. Our results highlight the potential pitfalls of adaptivity in analyzing data from quantum experiments and provide new algorithmic tools to safeguard against erroneous predictions in quantum experiments.

Agnostic Process Tomography

Characterizing a quantum system by learning its state or evolution is a fundamental problem in quantum physics and learning theory with a myriad of applications. Recently, as a new approach to this problem, the task of agnostic state tomography was defined, in which one aims to approximate an arbitrary quantum state by a simpler one in a given class. Generalizing this notion to quantum processes, we initiate the study of agnostic process tomography: given query access to an unknown quantum channel $\Phi$ and a known concept class $\mathcal{C}$ of channels, output a quantum channel that approximates $\Phi$ as well as any channel in the concept class $\mathcal{C}$, up to some error. In this work, we propose several natural applications for this new task in quantum machine learning, quantum metrology, classical simulation, and error mitigation. In addition, we give efficient agnostic process tomography algorithms for a wide variety of concept classes, including Pauli strings, Pauli channels, quantum junta channels, low-degree channels, and a class of channels produced by $\mathsf{QAC}^0$ circuits. The main technical tool we use is Pauli spectrum analysis of operators and superoperators. We also prove that, using ancilla qubits, any agnostic state tomography algorithm can be extended to one solving agnostic process tomography for a compatible concept class of unitaries, immediately giving us efficient agnostic learning algorithms for Clifford circuits, Clifford circuits with few T gates, and circuits consisting of a tensor product of single-qubit gates. Together, our results provide insight into the conditions and new algorithms necessary to extend the learnability of a concept class from the standard tomographic setting to the agnostic one.

Predicting Ground State Properties: Constant Sample Complexity and Deep Learning Algorithms

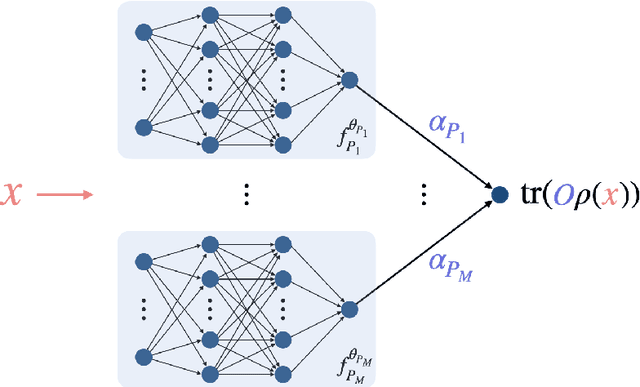
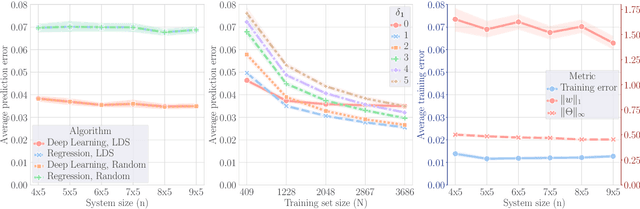
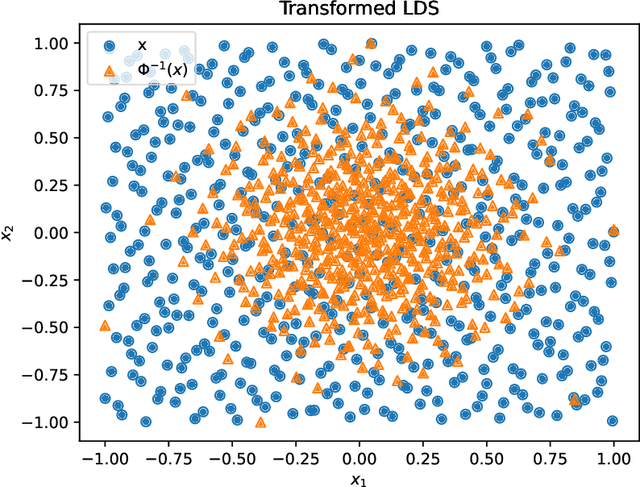
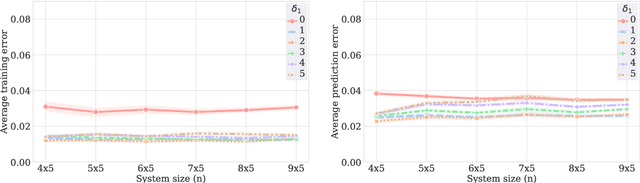
A fundamental problem in quantum many-body physics is that of finding ground states of local Hamiltonians. A number of recent works gave provably efficient machine learning (ML) algorithms for learning ground states. Specifically, [Huang et al. Science 2022], introduced an approach for learning properties of the ground state of an $n$-qubit gapped local Hamiltonian $H$ from only $n^{\mathcal{O}(1)}$ data points sampled from Hamiltonians in the same phase of matter. This was subsequently improved by [Lewis et al. Nature Communications 2024], to $\mathcal{O}(\log n)$ samples when the geometry of the $n$-qubit system is known. In this work, we introduce two approaches that achieve a constant sample complexity, independent of system size $n$, for learning ground state properties. Our first algorithm consists of a simple modification of the ML model used by Lewis et al. and applies to a property of interest known beforehand. Our second algorithm, which applies even if a description of the property is not known, is a deep neural network model. While empirical results showing the performance of neural networks have been demonstrated, to our knowledge, this is the first rigorous sample complexity bound on a neural network model for predicting ground state properties. We also perform numerical experiments that confirm the improved scaling of our approach compared to earlier results.

Learning quantum states and unitaries of bounded gate complexity

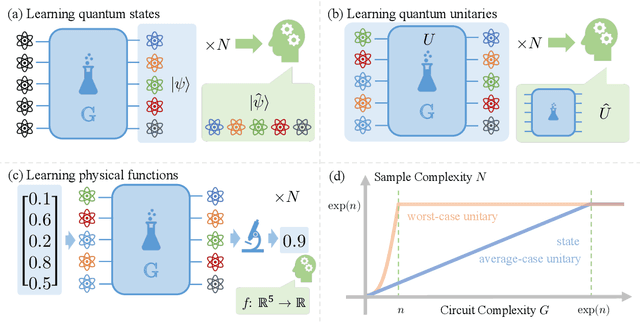
While quantum state tomography is notoriously hard, most states hold little interest to practically-minded tomographers. Given that states and unitaries appearing in Nature are of bounded gate complexity, it is natural to ask if efficient learning becomes possible. In this work, we prove that to learn a state generated by a quantum circuit with $G$ two-qubit gates to a small trace distance, a sample complexity scaling linearly in $G$ is necessary and sufficient. We also prove that the optimal query complexity to learn a unitary generated by $G$ gates to a small average-case error scales linearly in $G$. While sample-efficient learning can be achieved, we show that under reasonable cryptographic conjectures, the computational complexity for learning states and unitaries of gate complexity $G$ must scale exponentially in $G$. We illustrate how these results establish fundamental limitations on the expressivity of quantum machine learning models and provide new perspectives on no-free-lunch theorems in unitary learning. Together, our results answer how the complexity of learning quantum states and unitaries relate to the complexity of creating these states and unitaries.

Improved machine learning algorithm for predicting ground state properties

Finding the ground state of a quantum many-body system is a fundamental problem in quantum physics. In this work, we give a classical machine learning (ML) algorithm for predicting ground state properties with an inductive bias encoding geometric locality. The proposed ML model can efficiently predict ground state properties of an $n$-qubit gapped local Hamiltonian after learning from only $\mathcal{O}(\log(n))$ data about other Hamiltonians in the same quantum phase of matter. This improves substantially upon previous results that require $\mathcal{O}(n^c)$ data for a large constant $c$. Furthermore, the training and prediction time of the proposed ML model scale as $\mathcal{O}(n \log n)$ in the number of qubits $n$. Numerical experiments on physical systems with up to 45 qubits confirm the favorable scaling in predicting ground state properties using a small training dataset.