Predicting adaptively chosen observables in quantum systems

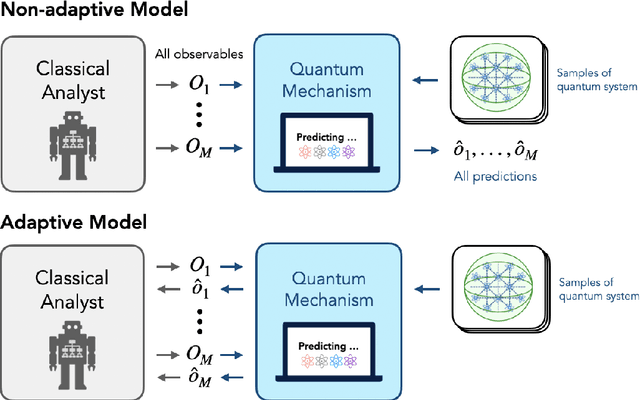
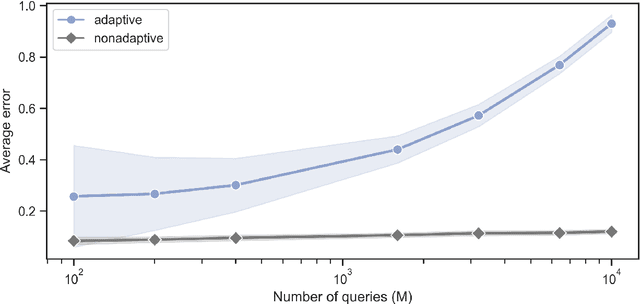
Recent advances have demonstrated that $\mathcal{O}(\log M)$ measurements suffice to predict $M$ properties of arbitrarily large quantum many-body systems. However, these remarkable findings assume that the properties to be predicted are chosen independently of the data. This assumption can be violated in practice, where scientists adaptively select properties after looking at previous predictions. This work investigates the adaptive setting for three classes of observables: local, Pauli, and bounded-Frobenius-norm observables. We prove that $\Omega(\sqrt{M})$ samples of an arbitrarily large unknown quantum state are necessary to predict expectation values of $M$ adaptively chosen local and Pauli observables. We also present computationally-efficient algorithms that achieve this information-theoretic lower bound. In contrast, for bounded-Frobenius-norm observables, we devise an algorithm requiring only $\mathcal{O}(\log M)$ samples, independent of system size. Our results highlight the potential pitfalls of adaptivity in analyzing data from quantum experiments and provide new algorithmic tools to safeguard against erroneous predictions in quantum experiments.

How to Construct Random Unitaries

The existence of pseudorandom unitaries (PRUs) -- efficient quantum circuits that are computationally indistinguishable from Haar-random unitaries -- has been a central open question, with significant implications for cryptography, complexity theory, and fundamental physics. In this work, we close this question by proving that PRUs exist, assuming that any quantum-secure one-way function exists. We establish this result for both (1) the standard notion of PRUs, which are secure against any efficient adversary that makes queries to the unitary $U$, and (2) a stronger notion of PRUs, which are secure even against adversaries that can query both the unitary $U$ and its inverse $U^\dagger$. In the process, we prove that any algorithm that makes queries to a Haar-random unitary can be efficiently simulated on a quantum computer, up to inverse-exponential trace distance.

Predicting quantum channels over general product distributions

We investigate the problem of predicting the output behavior of unknown quantum channels. Given query access to an $n$-qubit channel $E$ and an observable $O$, we aim to learn the mapping \begin{equation*} \rho \mapsto \mathrm{Tr}(O E[\rho]) \end{equation*} to within a small error for most $\rho$ sampled from a distribution $D$. Previously, Huang, Chen, and Preskill proved a surprising result that even if $E$ is arbitrary, this task can be solved in time roughly $n^{O(\log(1/\epsilon))}$, where $\epsilon$ is the target prediction error. However, their guarantee applied only to input distributions $D$ invariant under all single-qubit Clifford gates, and their algorithm fails for important cases such as general product distributions over product states $\rho$. In this work, we propose a new approach that achieves accurate prediction over essentially any product distribution $D$, provided it is not "classical" in which case there is a trivial exponential lower bound. Our method employs a "biased Pauli analysis," analogous to classical biased Fourier analysis. Implementing this approach requires overcoming several challenges unique to the quantum setting, including the lack of a basis with appropriate orthogonality properties. The techniques we develop to address these issues may have broader applications in quantum information.

Certifying almost all quantum states with few single-qubit measurements

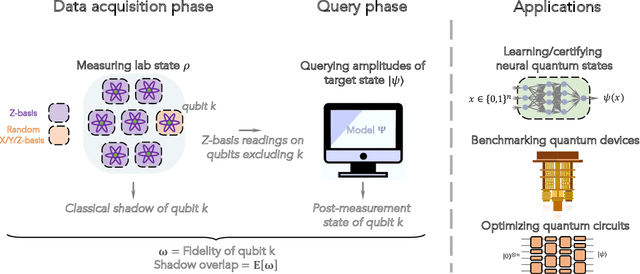
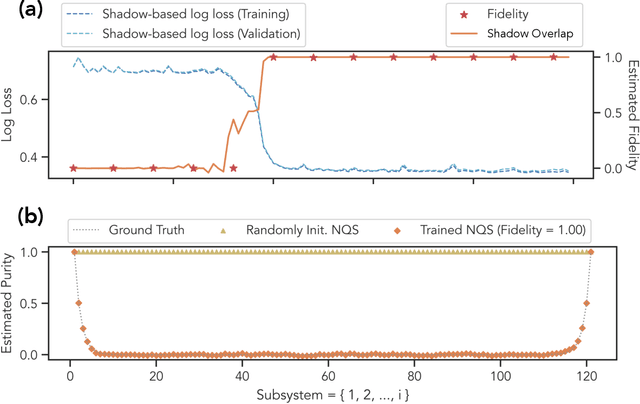
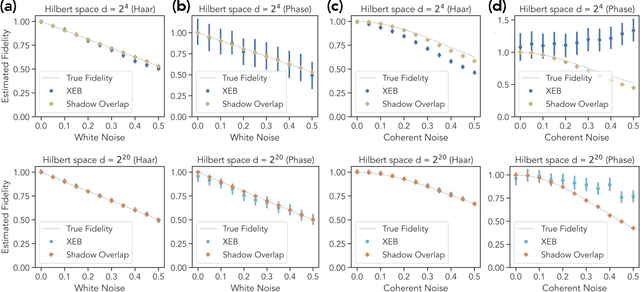
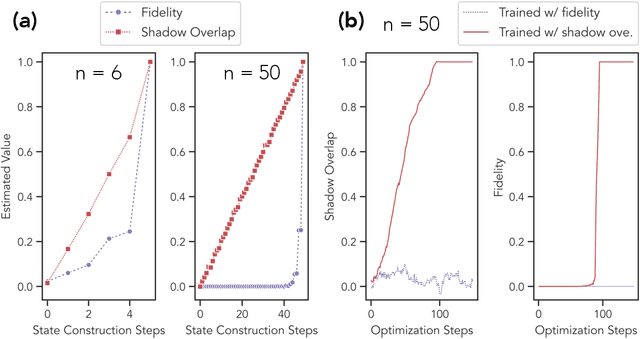
Certifying that an n-qubit state synthesized in the lab is close to the target state is a fundamental task in quantum information science. However, existing rigorous protocols either require deep quantum circuits or exponentially many single-qubit measurements. In this work, we prove that almost all n-qubit target states, including those with exponential circuit complexity, can be certified from only O(n^2) single-qubit measurements. This result is established by a new technique that relates certification to the mixing time of a random walk. Our protocol has applications for benchmarking quantum systems, for optimizing quantum circuits to generate a desired target state, and for learning and verifying neural networks, tensor networks, and various other representations of quantum states using only single-qubit measurements. We show that such verified representations can be used to efficiently predict highly non-local properties that would otherwise require an exponential number of measurements. We demonstrate these applications in numerical experiments with up to 120 qubits, and observe advantage over existing methods such as cross-entropy benchmarking (XEB).

Learning shallow quantum circuits

Despite fundamental interests in learning quantum circuits, the existence of a computationally efficient algorithm for learning shallow quantum circuits remains an open question. Because shallow quantum circuits can generate distributions that are classically hard to sample from, existing learning algorithms do not apply. In this work, we present a polynomial-time classical algorithm for learning the description of any unknown $n$-qubit shallow quantum circuit $U$ (with arbitrary unknown architecture) within a small diamond distance using single-qubit measurement data on the output states of $U$. We also provide a polynomial-time classical algorithm for learning the description of any unknown $n$-qubit state $\lvert \psi \rangle = U \lvert 0^n \rangle$ prepared by a shallow quantum circuit $U$ (on a 2D lattice) within a small trace distance using single-qubit measurements on copies of $\lvert \psi \rangle$. Our approach uses a quantum circuit representation based on local inversions and a technique to combine these inversions. This circuit representation yields an optimization landscape that can be efficiently navigated and enables efficient learning of quantum circuits that are classically hard to simulate.

Learning quantum states and unitaries of bounded gate complexity

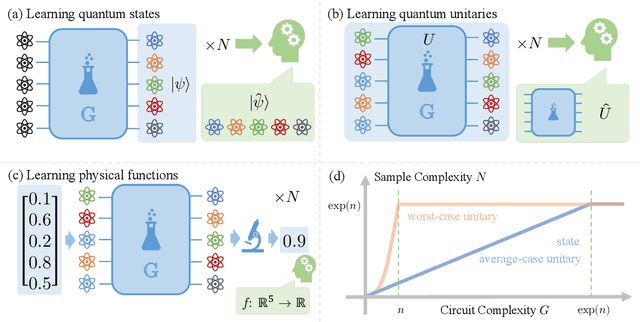
While quantum state tomography is notoriously hard, most states hold little interest to practically-minded tomographers. Given that states and unitaries appearing in Nature are of bounded gate complexity, it is natural to ask if efficient learning becomes possible. In this work, we prove that to learn a state generated by a quantum circuit with $G$ two-qubit gates to a small trace distance, a sample complexity scaling linearly in $G$ is necessary and sufficient. We also prove that the optimal query complexity to learn a unitary generated by $G$ gates to a small average-case error scales linearly in $G$. While sample-efficient learning can be achieved, we show that under reasonable cryptographic conjectures, the computational complexity for learning states and unitaries of gate complexity $G$ must scale exponentially in $G$. We illustrate how these results establish fundamental limitations on the expressivity of quantum machine learning models and provide new perspectives on no-free-lunch theorems in unitary learning. Together, our results answer how the complexity of learning quantum states and unitaries relate to the complexity of creating these states and unitaries.

Tight bounds on Pauli channel learning without entanglement

Entanglement is a useful resource for learning, but a precise characterization of its advantage can be challenging. In this work, we consider learning algorithms without entanglement to be those that only utilize separable states, measurements, and operations between the main system of interest and an ancillary system. These algorithms are equivalent to those that apply quantum circuits on the main system interleaved with mid-circuit measurements and classical feedforward. We prove a tight lower bound for learning Pauli channels without entanglement that closes a cubic gap between the best-known upper and lower bound. In particular, we show that $\Theta(2^n\varepsilon^{-2})$ rounds of measurements are required to estimate each eigenvalue of an $n$-qubit Pauli channel to $\varepsilon$ error with high probability when learning without entanglement. In contrast, a learning algorithm with entanglement only needs $\Theta(\varepsilon^{-2})$ rounds of measurements. The tight lower bound strengthens the foundation for an experimental demonstration of entanglement-enhanced advantages for characterizing Pauli noise.

On quantum backpropagation, information reuse, and cheating measurement collapse

The success of modern deep learning hinges on the ability to train neural networks at scale. Through clever reuse of intermediate information, backpropagation facilitates training through gradient computation at a total cost roughly proportional to running the function, rather than incurring an additional factor proportional to the number of parameters - which can now be in the trillions. Naively, one expects that quantum measurement collapse entirely rules out the reuse of quantum information as in backpropagation. But recent developments in shadow tomography, which assumes access to multiple copies of a quantum state, have challenged that notion. Here, we investigate whether parameterized quantum models can train as efficiently as classical neural networks. We show that achieving backpropagation scaling is impossible without access to multiple copies of a state. With this added ability, we introduce an algorithm with foundations in shadow tomography that matches backpropagation scaling in quantum resources while reducing classical auxiliary computational costs to open problems in shadow tomography. These results highlight the nuance of reusing quantum information for practical purposes and clarify the unique difficulties in training large quantum models, which could alter the course of quantum machine learning.

The power and limitations of learning quantum dynamics incoherently

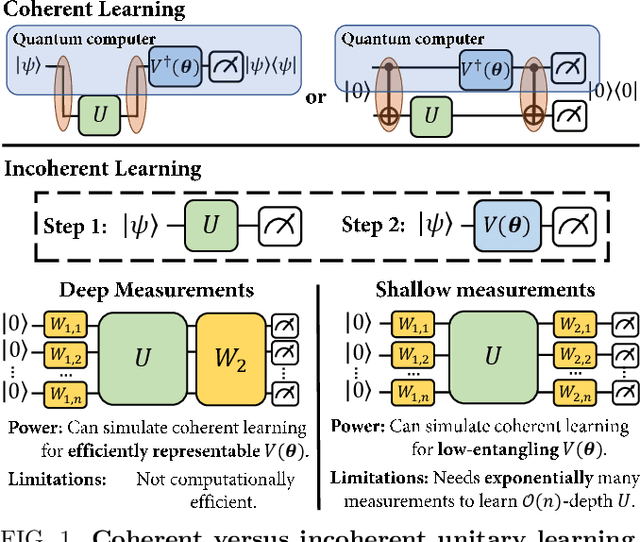
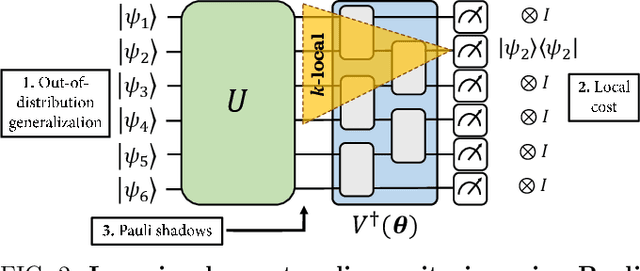
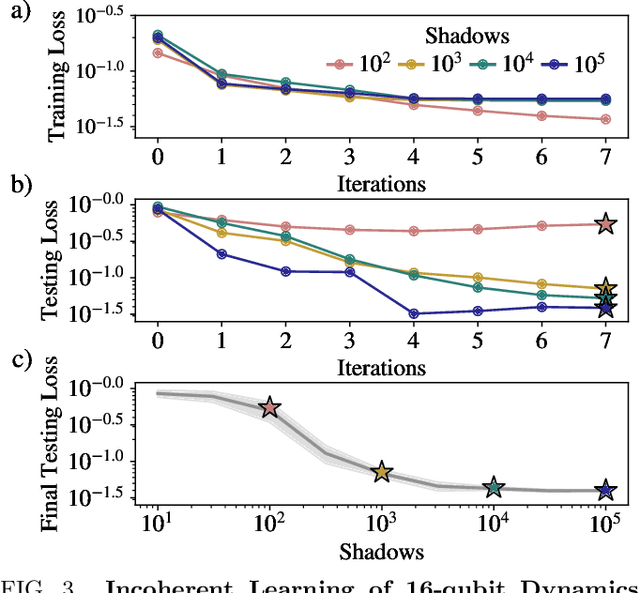
Quantum process learning is emerging as an important tool to study quantum systems. While studied extensively in coherent frameworks, where the target and model system can share quantum information, less attention has been paid to whether the dynamics of quantum systems can be learned without the system and target directly interacting. Such incoherent frameworks are practically appealing since they open up methods of transpiling quantum processes between the different physical platforms without the need for technically challenging hybrid entanglement schemes. Here we provide bounds on the sample complexity of learning unitary processes incoherently by analyzing the number of measurements that are required to emulate well-established coherent learning strategies. We prove that if arbitrary measurements are allowed, then any efficiently representable unitary can be efficiently learned within the incoherent framework; however, when restricted to shallow-depth measurements only low-entangling unitaries can be learned. We demonstrate our incoherent learning algorithm for low entangling unitaries by successfully learning a 16-qubit unitary on \texttt{ibmq\_kolkata}, and further demonstrate the scalabilty of our proposed algorithm through extensive numerical experiments.

Challenges and Opportunities in Quantum Machine Learning

At the intersection of machine learning and quantum computing, Quantum Machine Learning (QML) has the potential of accelerating data analysis, especially for quantum data, with applications for quantum materials, biochemistry, and high-energy physics. Nevertheless, challenges remain regarding the trainability of QML models. Here we review current methods and applications for QML. We highlight differences between quantum and classical machine learning, with a focus on quantum neural networks and quantum deep learning. Finally, we discuss opportunities for quantum advantage with QML.