Learning to erase quantum states: thermodynamic implications of quantum learning theory

The energy cost of erasing quantum states depends on our knowledge of the states. We show that learning algorithms can acquire such knowledge to erase many copies of an unknown state at the optimal energy cost. This is proved by showing that learning can be made fully reversible and has no fundamental energy cost itself. With simple counting arguments, we relate the energy cost of erasing quantum states to their complexity, entanglement, and magic. We further show that the constructed erasure protocol is computationally efficient when learning is efficient. Conversely, under standard cryptographic assumptions, we prove that the optimal energy cost cannot be achieved efficiently in general. These results also enable efficient work extraction based on learning. Together, our results establish a concrete connection between quantum learning theory and thermodynamics, highlighting the physical significance of learning processes and enabling efficient learning-based protocols for thermodynamic tasks.

When can classical neural networks represent quantum states?

A naive classical representation of an n-qubit state requires specifying exponentially many amplitudes in the computational basis. Past works have demonstrated that classical neural networks can succinctly express these amplitudes for many physically relevant states, leading to computationally powerful representations known as neural quantum states. What underpins the efficacy of such representations? We show that conditional correlations present in the measurement distribution of quantum states control the performance of their neural representations. Such conditional correlations are basis dependent, arise due to measurement-induced entanglement, and reveal features not accessible through conventional few-body correlations often examined in studies of phases of matter. By combining theoretical and numerical analysis, we demonstrate how the state's entanglement and sign structure, along with the choice of measurement basis, give rise to distinct patterns of short- or long-range conditional correlations. Our findings provide a rigorous framework for exploring the expressive power of neural quantum states.

Learning $k$-body Hamiltonians via compressed sensing

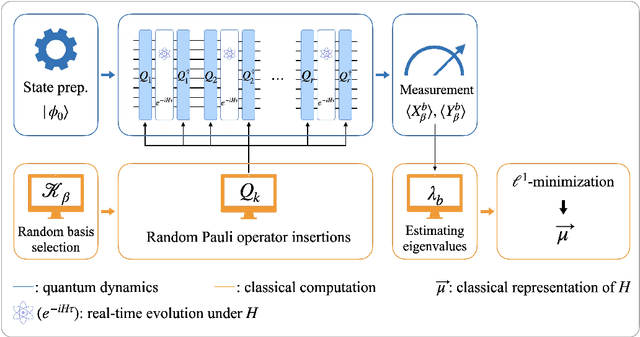
We study the problem of learning a $k$-body Hamiltonian with $M$ unknown Pauli terms that are not necessarily geometrically local. We propose a protocol that learns the Hamiltonian to precision $\epsilon$ with total evolution time ${\mathcal{O}}(M^{1/2+1/p}/\epsilon)$ up to logarithmic factors, where the error is quantified by the $\ell^p$-distance between Pauli coefficients. Our learning protocol uses only single-qubit control operations and a GHZ state initial state, is non-adaptive, is robust against SPAM errors, and performs well even if $M$ and $k$ are not precisely known in advance or if the Hamiltonian is not exactly $M$-sparse. Methods from the classical theory of compressed sensing are used for efficiently identifying the $M$ terms in the Hamiltonian from among all possible $k$-body Pauli operators. We also provide a lower bound on the total evolution time needed in this learning task, and we discuss the operational interpretations of the $\ell^1$ and $\ell^2$ error metrics. In contrast to previous works, our learning protocol requires neither geometric locality nor any other relaxed locality conditions.

Predicting adaptively chosen observables in quantum systems

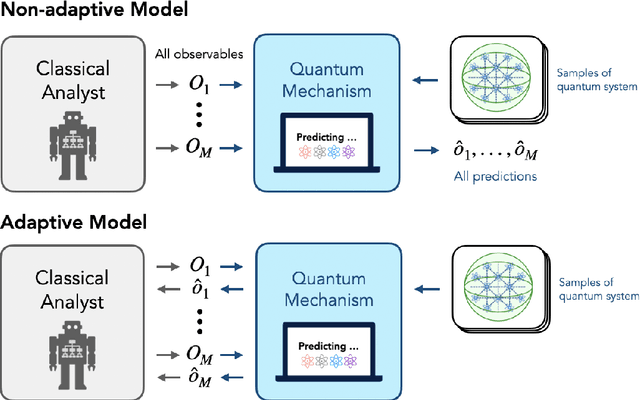
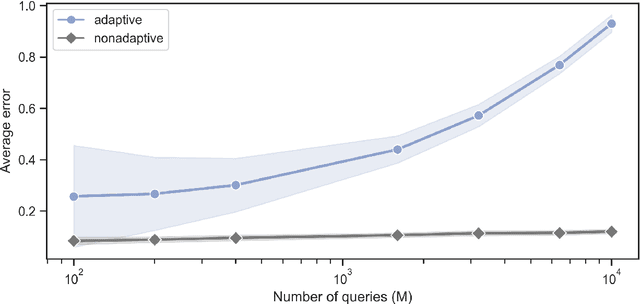
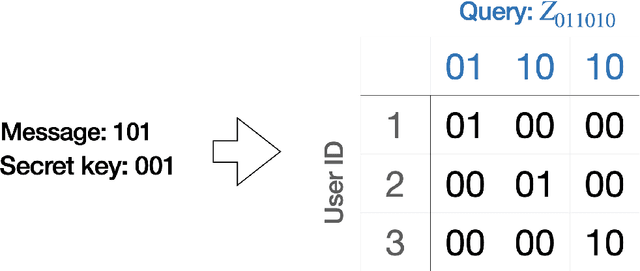
Recent advances have demonstrated that $\mathcal{O}(\log M)$ measurements suffice to predict $M$ properties of arbitrarily large quantum many-body systems. However, these remarkable findings assume that the properties to be predicted are chosen independently of the data. This assumption can be violated in practice, where scientists adaptively select properties after looking at previous predictions. This work investigates the adaptive setting for three classes of observables: local, Pauli, and bounded-Frobenius-norm observables. We prove that $\Omega(\sqrt{M})$ samples of an arbitrarily large unknown quantum state are necessary to predict expectation values of $M$ adaptively chosen local and Pauli observables. We also present computationally-efficient algorithms that achieve this information-theoretic lower bound. In contrast, for bounded-Frobenius-norm observables, we devise an algorithm requiring only $\mathcal{O}(\log M)$ samples, independent of system size. Our results highlight the potential pitfalls of adaptivity in analyzing data from quantum experiments and provide new algorithmic tools to safeguard against erroneous predictions in quantum experiments.

Certifying almost all quantum states with few single-qubit measurements

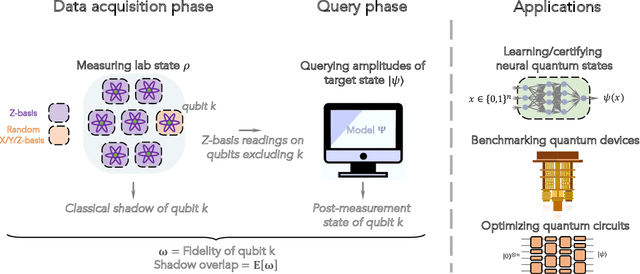
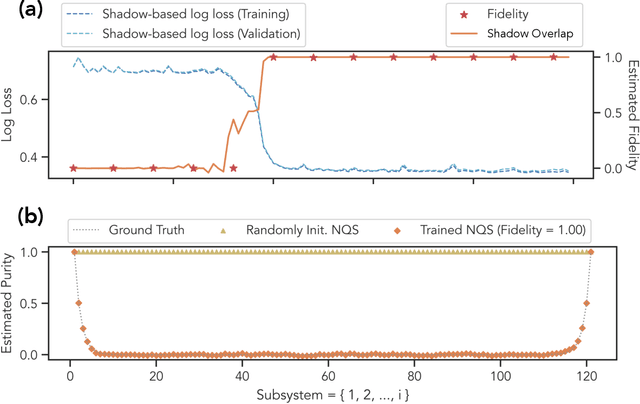
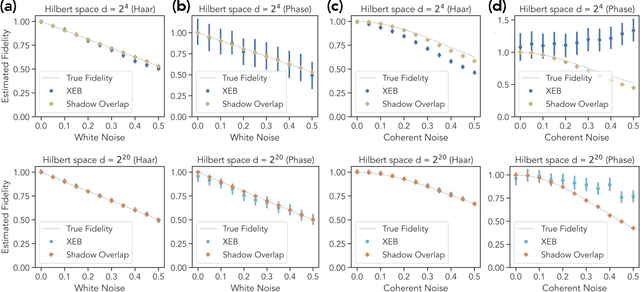
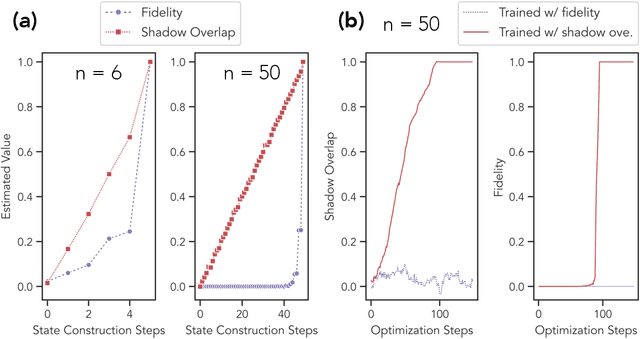
Certifying that an n-qubit state synthesized in the lab is close to the target state is a fundamental task in quantum information science. However, existing rigorous protocols either require deep quantum circuits or exponentially many single-qubit measurements. In this work, we prove that almost all n-qubit target states, including those with exponential circuit complexity, can be certified from only O(n^2) single-qubit measurements. This result is established by a new technique that relates certification to the mixing time of a random walk. Our protocol has applications for benchmarking quantum systems, for optimizing quantum circuits to generate a desired target state, and for learning and verifying neural networks, tensor networks, and various other representations of quantum states using only single-qubit measurements. We show that such verified representations can be used to efficiently predict highly non-local properties that would otherwise require an exponential number of measurements. We demonstrate these applications in numerical experiments with up to 120 qubits, and observe advantage over existing methods such as cross-entropy benchmarking (XEB).

Improved machine learning algorithm for predicting ground state properties

Finding the ground state of a quantum many-body system is a fundamental problem in quantum physics. In this work, we give a classical machine learning (ML) algorithm for predicting ground state properties with an inductive bias encoding geometric locality. The proposed ML model can efficiently predict ground state properties of an $n$-qubit gapped local Hamiltonian after learning from only $\mathcal{O}(\log(n))$ data about other Hamiltonians in the same quantum phase of matter. This improves substantially upon previous results that require $\mathcal{O}(n^c)$ data for a large constant $c$. Furthermore, the training and prediction time of the proposed ML model scale as $\mathcal{O}(n \log n)$ in the number of qubits $n$. Numerical experiments on physical systems with up to 45 qubits confirm the favorable scaling in predicting ground state properties using a small training dataset.

Learning to predict arbitrary quantum processes

We present an efficient machine learning (ML) algorithm for predicting any unknown quantum process $\mathcal{E}$ over $n$ qubits. For a wide range of distributions $\mathcal{D}$ on arbitrary $n$-qubit states, we show that this ML algorithm can learn to predict any local property of the output from the unknown process $\mathcal{E}$, with a small average error over input states drawn from $\mathcal{D}$. The ML algorithm is computationally efficient even when the unknown process is a quantum circuit with exponentially many gates. Our algorithm combines efficient procedures for learning properties of an unknown state and for learning a low-degree approximation to an unknown observable. The analysis hinges on proving new norm inequalities, including a quantum analogue of the classical Bohnenblust-Hille inequality, which we derive by giving an improved algorithm for optimizing local Hamiltonians. Overall, our results highlight the potential for ML models to predict the output of complex quantum dynamics much faster than the time needed to run the process itself.

Foundations for learning from noisy quantum experiments

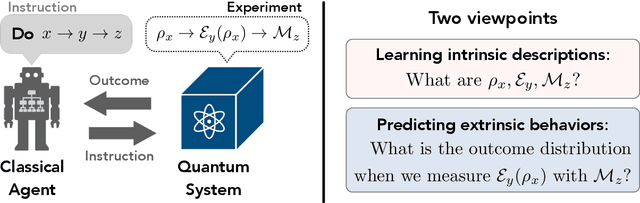
Understanding what can be learned from experiments is central to scientific progress. In this work, we use a learning-theoretic perspective to study the task of learning physical operations in a quantum machine when all operations (state preparation, dynamics, and measurement) are a priori unknown. We prove that, without any prior knowledge, if one can explore the full quantum state space by composing the operations, then every operation can be learned. When one cannot explore the full state space but all operations are approximately known and noise in Clifford gates is gate-independent, we find an efficient algorithm for learning all operations up to a single unlearnable parameter characterizing the fidelity of the initial state. For learning a noise channel on Clifford gates to a fixed accuracy, our algorithm uses quadratically fewer experiments than previously known protocols. Under more general conditions, the true description of the noise can be unlearnable; for example, we prove that no benchmarking protocol can learn gate-dependent Pauli noise on Clifford+T gates even under perfect state preparation and measurement. Despite not being able to learn the noise, we show that a noisy quantum computer that performs entangled measurements on multiple copies of an unknown state can yield a large advantage in learning properties of the state compared to a noiseless device that measures individual copies and then processes the measurement data using a classical computer. Concretely, we prove that noisy quantum computers with two-qubit gate error rate $\epsilon$ can achieve a learning task using $N$ copies of the state, while $N^{\Omega(1/\epsilon)}$ copies are required classically.

Quantum advantage in learning from experiments

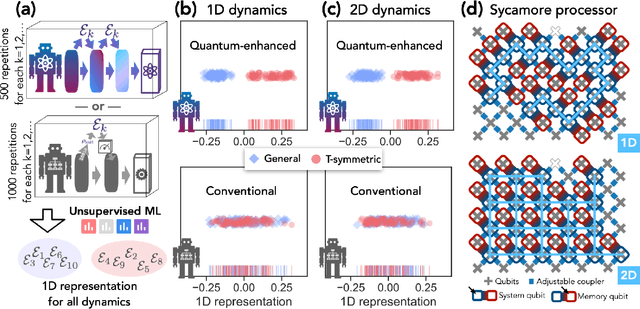
Quantum technology has the potential to revolutionize how we acquire and process experimental data to learn about the physical world. An experimental setup that transduces data from a physical system to a stable quantum memory, and processes that data using a quantum computer, could have significant advantages over conventional experiments in which the physical system is measured and the outcomes are processed using a classical computer. We prove that, in various tasks, quantum machines can learn from exponentially fewer experiments than those required in conventional experiments. The exponential advantage holds in predicting properties of physical systems, performing quantum principal component analysis on noisy states, and learning approximate models of physical dynamics. In some tasks, the quantum processing needed to achieve the exponential advantage can be modest; for example, one can simultaneously learn about many noncommuting observables by processing only two copies of the system. Conducting experiments with up to 40 superconducting qubits and 1300 quantum gates, we demonstrate that a substantial quantum advantage can be realized using today's relatively noisy quantum processors. Our results highlight how quantum technology can enable powerful new strategies to learn about nature.

Provably efficient machine learning for quantum many-body problems

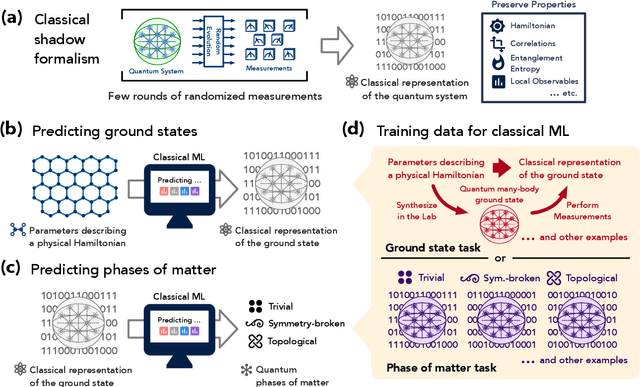
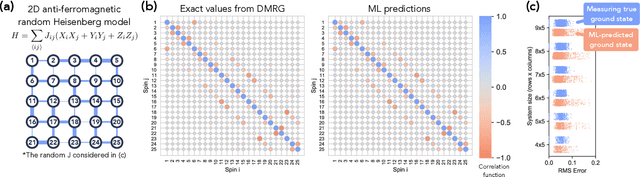
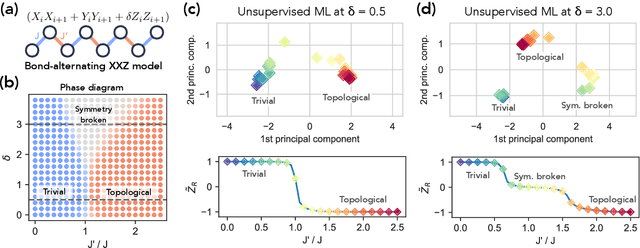
Classical machine learning (ML) provides a potentially powerful approach to solving challenging quantum many-body problems in physics and chemistry. However, the advantages of ML over more traditional methods have not been firmly established. In this work, we prove that classical ML algorithms can efficiently predict ground state properties of gapped Hamiltonians in finite spatial dimensions, after learning from data obtained by measuring other Hamiltonians in the same quantum phase of matter. In contrast, under widely accepted complexity theory assumptions, classical algorithms that do not learn from data cannot achieve the same guarantee. We also prove that classical ML algorithms can efficiently classify a wide range of quantum phases of matter. Our arguments are based on the concept of a classical shadow, a succinct classical description of a many-body quantum state that can be constructed in feasible quantum experiments and be used to predict many properties of the state. Extensive numerical experiments corroborate our theoretical results in a variety of scenarios, including Rydberg atom systems, 2D random Heisenberg models, symmetry-protected topological phases, and topologically ordered phases.