Richard Kueng
Quantum computing and artificial intelligence: status and perspectives
May 29, 2025


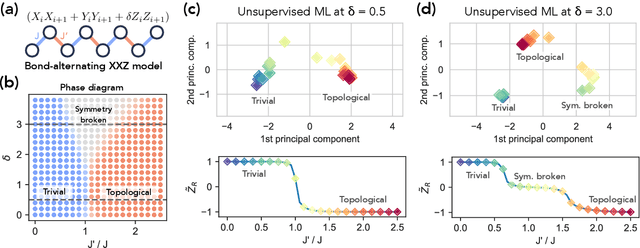
Abstract:This white paper discusses and explores the various points of intersection between quantum computing and artificial intelligence (AI). It describes how quantum computing could support the development of innovative AI solutions. It also examines use cases of classical AI that can empower research and development in quantum technologies, with a focus on quantum computing and quantum sensing. The purpose of this white paper is to provide a long-term research agenda aimed at addressing foundational questions about how AI and quantum computing interact and benefit one another. It concludes with a set of recommendations and challenges, including how to orchestrate the proposed theoretical work, align quantum AI developments with quantum hardware roadmaps, estimate both classical and quantum resources - especially with the goal of mitigating and optimizing energy consumption - advance this emerging hybrid software engineering discipline, and enhance European industrial competitiveness while considering societal implications.
On the average-case complexity of learning output distributions of quantum circuits
May 09, 2023Abstract:In this work, we show that learning the output distributions of brickwork random quantum circuits is average-case hard in the statistical query model. This learning model is widely used as an abstract computational model for most generic learning algorithms. In particular, for brickwork random quantum circuits on $n$ qubits of depth $d$, we show three main results: - At super logarithmic circuit depth $d=\omega(\log(n))$, any learning algorithm requires super polynomially many queries to achieve a constant probability of success over the randomly drawn instance. - There exists a $d=O(n)$, such that any learning algorithm requires $\Omega(2^n)$ queries to achieve a $O(2^{-n})$ probability of success over the randomly drawn instance. - At infinite circuit depth $d\to\infty$, any learning algorithm requires $2^{2^{\Omega(n)}}$ many queries to achieve a $2^{-2^{\Omega(n)}}$ probability of success over the randomly drawn instance. As an auxiliary result of independent interest, we show that the output distribution of a brickwork random quantum circuit is constantly far from any fixed distribution in total variation distance with probability $1-O(2^{-n})$, which confirms a variant of a conjecture by Aaronson and Chen.
Improved machine learning algorithm for predicting ground state properties
Jan 30, 2023Abstract:Finding the ground state of a quantum many-body system is a fundamental problem in quantum physics. In this work, we give a classical machine learning (ML) algorithm for predicting ground state properties with an inductive bias encoding geometric locality. The proposed ML model can efficiently predict ground state properties of an $n$-qubit gapped local Hamiltonian after learning from only $\mathcal{O}(\log(n))$ data about other Hamiltonians in the same quantum phase of matter. This improves substantially upon previous results that require $\mathcal{O}(n^c)$ data for a large constant $c$. Furthermore, the training and prediction time of the proposed ML model scale as $\mathcal{O}(n \log n)$ in the number of qubits $n$. Numerical experiments on physical systems with up to 45 qubits confirm the favorable scaling in predicting ground state properties using a small training dataset.
Quantum advantage in learning from experiments
Dec 01, 2021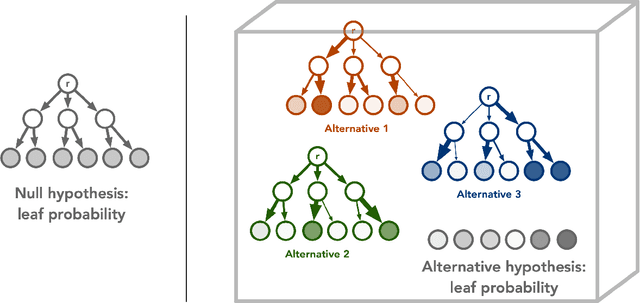
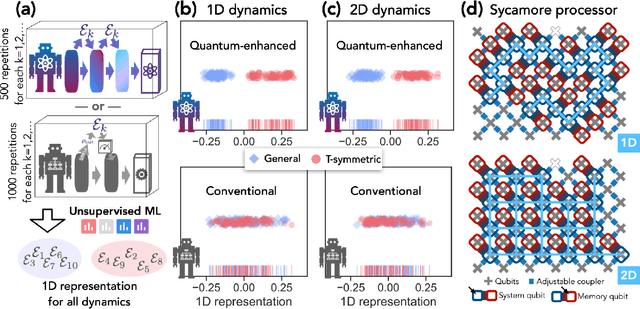

Abstract:Quantum technology has the potential to revolutionize how we acquire and process experimental data to learn about the physical world. An experimental setup that transduces data from a physical system to a stable quantum memory, and processes that data using a quantum computer, could have significant advantages over conventional experiments in which the physical system is measured and the outcomes are processed using a classical computer. We prove that, in various tasks, quantum machines can learn from exponentially fewer experiments than those required in conventional experiments. The exponential advantage holds in predicting properties of physical systems, performing quantum principal component analysis on noisy states, and learning approximate models of physical dynamics. In some tasks, the quantum processing needed to achieve the exponential advantage can be modest; for example, one can simultaneously learn about many noncommuting observables by processing only two copies of the system. Conducting experiments with up to 40 superconducting qubits and 1300 quantum gates, we demonstrate that a substantial quantum advantage can be realized using today's relatively noisy quantum processors. Our results highlight how quantum technology can enable powerful new strategies to learn about nature.
Provably efficient machine learning for quantum many-body problems
Jul 18, 2021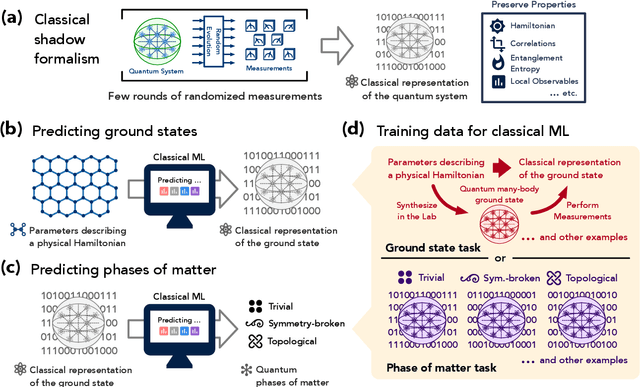

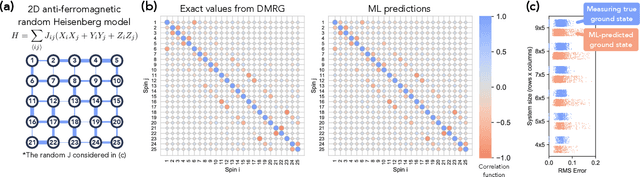
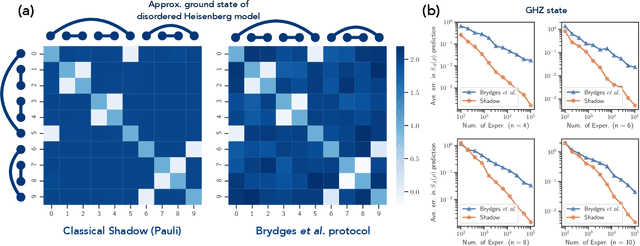
Abstract:Classical machine learning (ML) provides a potentially powerful approach to solving challenging quantum many-body problems in physics and chemistry. However, the advantages of ML over more traditional methods have not been firmly established. In this work, we prove that classical ML algorithms can efficiently predict ground state properties of gapped Hamiltonians in finite spatial dimensions, after learning from data obtained by measuring other Hamiltonians in the same quantum phase of matter. In contrast, under widely accepted complexity theory assumptions, classical algorithms that do not learn from data cannot achieve the same guarantee. We also prove that classical ML algorithms can efficiently classify a wide range of quantum phases of matter. Our arguments are based on the concept of a classical shadow, a succinct classical description of a many-body quantum state that can be constructed in feasible quantum experiments and be used to predict many properties of the state. Extensive numerical experiments corroborate our theoretical results in a variety of scenarios, including Rydberg atom systems, 2D random Heisenberg models, symmetry-protected topological phases, and topologically ordered phases.
Proof methods for robust low-rank matrix recovery
Jun 08, 2021
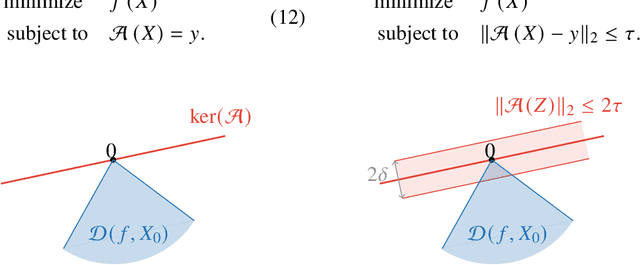
Abstract:Low-rank matrix recovery problems arise naturally as mathematical formulations of various inverse problems, such as matrix completion, blind deconvolution, and phase retrieval. Over the last two decades, a number of works have rigorously analyzed the reconstruction performance for such scenarios, giving rise to a rather general understanding of the potential and the limitations of low-rank matrix models in sensing problems. In this article, we compare the two main proof techniques that have been paving the way to a rigorous analysis, discuss their potential and limitations, and survey their successful applications. On the one hand, we review approaches based on descent cone analysis, showing that they often lead to strong guarantees even in the presence of adversarial noise, but face limitations when it comes to structured observations. On the other hand, we discuss techniques using approximate dual certificates and the golfing scheme, which are often better suited to deal with practical measurement structures, but sometimes lead to weaker guarantees. Lastly, we review recent progress towards analyzing descent cones also for structured scenarios -- exploiting the idea of splitting the cones into multiple parts that are analyzed via different techniques.
Information-theoretic bounds on quantum advantage in machine learning
Jan 07, 2021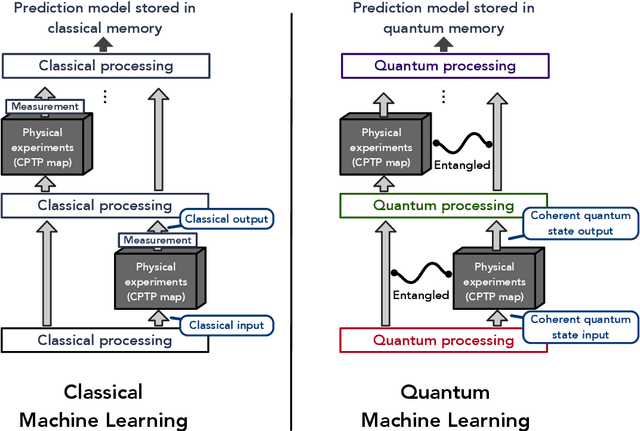
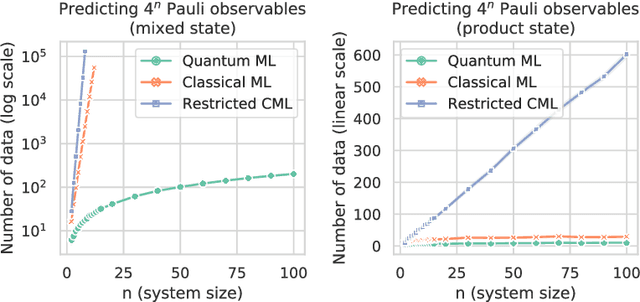
Abstract:We study the complexity of training classical and quantum machine learning (ML) models for predicting outcomes of physical experiments. The experiments depend on an input parameter $x$ and involve the execution of a (possibly unknown) quantum process $\mathcal{E}$. Our figure of merit is the number of runs of $\mathcal{E}$ during training, disregarding other measures of runtime. A classical ML model performs a measurement and records the classical outcome after each run of $\mathcal{E}$, while a quantum ML model can access $\mathcal{E}$ coherently to acquire quantum data; the classical or quantum data is then used to predict outcomes of future experiments. We prove that, for any input distribution $\mathcal{D}(x)$, a classical ML model can provide accurate predictions on average by accessing $\mathcal{E}$ a number of times comparable to the optimal quantum ML model. In contrast, for achieving accurate prediction on all inputs, we show that exponential quantum advantage is possible for certain tasks. For example, to predict expectation values of all Pauli observables in an $n$-qubit system $\rho$, we present a quantum ML model using only $\mathcal{O}(n)$ copies of $\rho$ and prove that classical ML models require $2^{\Omega(n)}$ copies.
Predicting Many Properties of a Quantum System from Very Few Measurements
Feb 18, 2020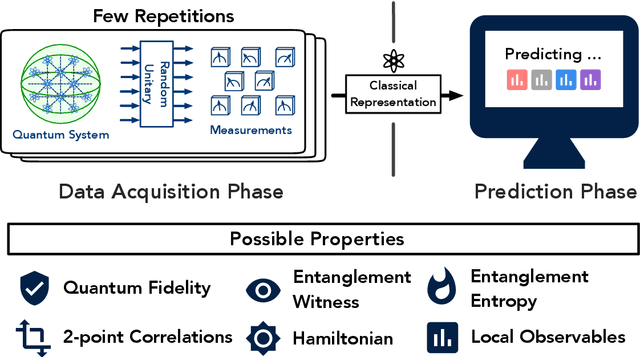

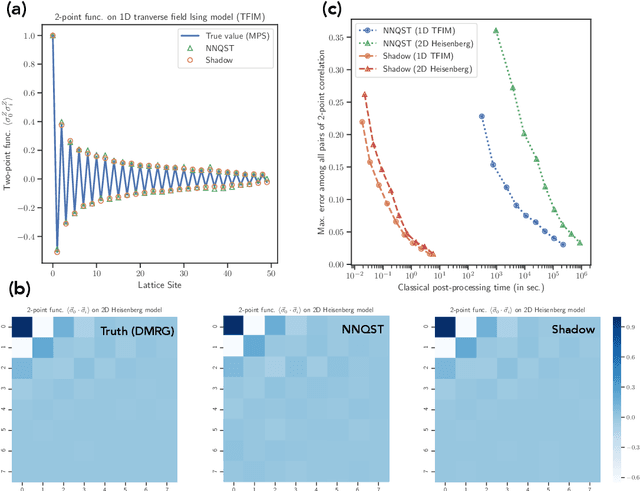
Abstract:Predicting properties of complex, large-scale quantum systems is essential for developing quantum technologies. We present an efficient method for constructing an approximate classical description of a quantum state using very few measurements of the state. This description, called a classical shadow, can be used to predict many different properties: order $\log M$ measurements suffice to accurately predict $M$ different functions of the state with high success probability. The number of measurements is independent of the system size, and saturates information-theoretic lower bounds. Moreover, target properties to predict can be selected after the measurements are completed. We support our theoretical findings with extensive numerical experiments. We apply classical shadows to predict quantum fidelities, entanglement entropies, two-point correlation functions, expectation values of local observables, and the energy variance of many-body local Hamiltonians, which allows applications to speedup variational quantum algorithms. The numerical results highlight the advantages of classical shadows relative to previously known methods.
Predicting Features of Quantum Systems using Classical Shadows
Aug 23, 2019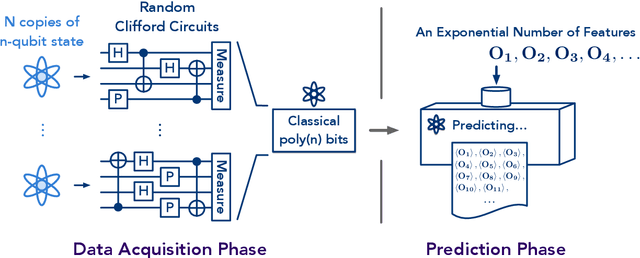
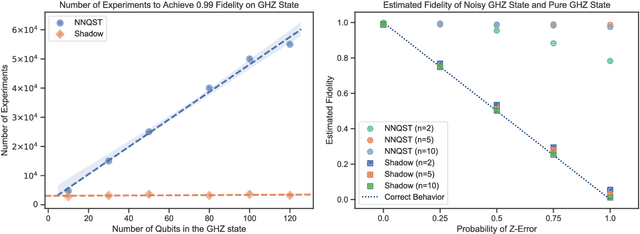
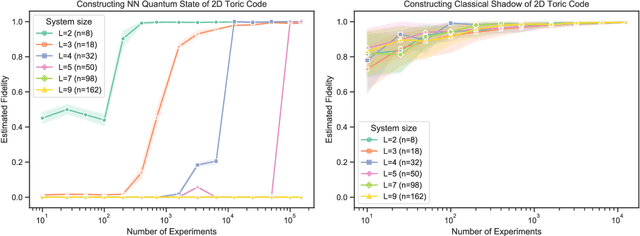
Abstract:Predicting features of complex, large-scale quantum systems is essential to the characterization and engineering of quantum architectures. We present an efficient approach for predicting a large number of linear features using classical shadows obtained from very few quantum measurements. This approach is guaranteed to accurately predict $M$ linear functions with bounded Hilbert-Schmidt norm from only $\log (M)$ measurement repetitions. This sampling rate is completely independent of the system size and saturates fundamental lower bounds from information theory. We support our theoretical findings with numerical experiments over a wide range of problem sizes (2 to 162 qubits). These highlight advantages compared to existing machine learning approaches.
A unifying framework for relaxations of the causal assumptions in Bell's theorem
Nov 17, 2014

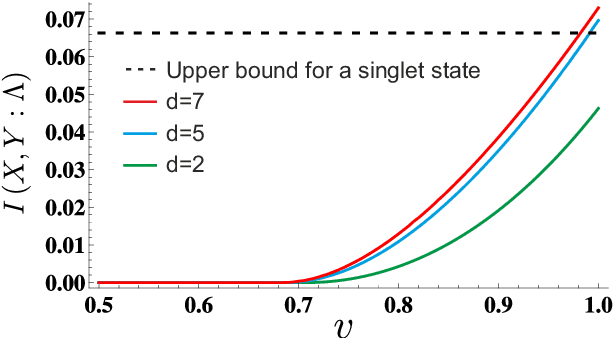
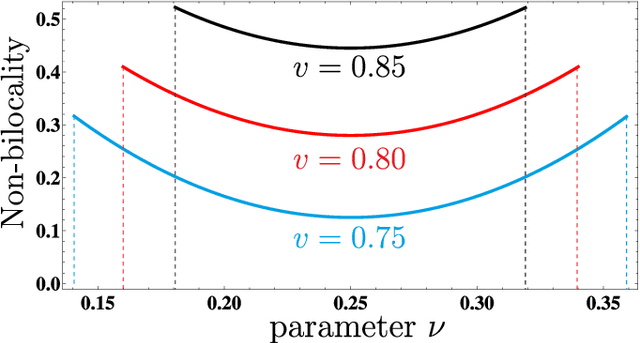
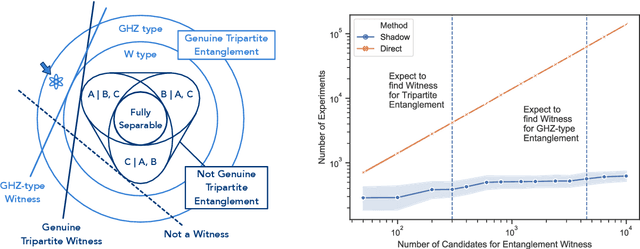
Abstract:Bell's Theorem shows that quantum mechanical correlations can violate the constraints that the causal structure of certain experiments impose on any classical explanation. It is thus natural to ask to which degree the causal assumptions -- e.g. locality or measurement independence -- have to be relaxed in order to allow for a classical description of such experiments. Here, we develop a conceptual and computational framework for treating this problem. We employ the language of Bayesian networks to systematically construct alternative causal structures and bound the degree of relaxation using quantitative measures that originate from the mathematical theory of causality. The main technical insight is that the resulting problems can often be expressed as computationally tractable linear programs. We demonstrate the versatility of the framework by applying it to a variety of scenarios, ranging from relaxations of the measurement independence, locality and bilocality assumptions, to a novel causal interpretation of CHSH inequality violations.
* 6 pages + appendix, 5 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge