Generative quantum advantage for classical and quantum problems

Recent breakthroughs in generative machine learning, powered by massive computational resources, have demonstrated unprecedented human-like capabilities. While beyond-classical quantum experiments can generate samples from classically intractable distributions, their complexity has thwarted all efforts toward efficient learning. This challenge has hindered demonstrations of generative quantum advantage: the ability of quantum computers to learn and generate desired outputs substantially better than classical computers. We resolve this challenge by introducing families of generative quantum models that are hard to simulate classically, are efficiently trainable, exhibit no barren plateaus or proliferating local minima, and can learn to generate distributions beyond the reach of classical computers. Using a $68$-qubit superconducting quantum processor, we demonstrate these capabilities in two scenarios: learning classically intractable probability distributions and learning quantum circuits for accelerated physical simulation. Our results establish that both learning and sampling can be performed efficiently in the beyond-classical regime, opening new possibilities for quantum-enhanced generative models with provable advantage.

Quantum advantage in learning from experiments

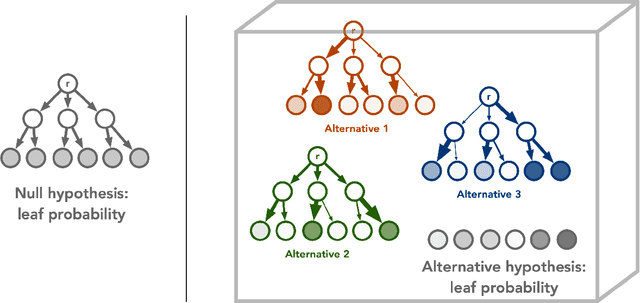
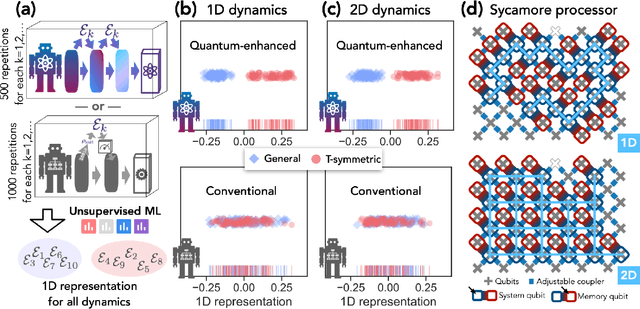
Quantum technology has the potential to revolutionize how we acquire and process experimental data to learn about the physical world. An experimental setup that transduces data from a physical system to a stable quantum memory, and processes that data using a quantum computer, could have significant advantages over conventional experiments in which the physical system is measured and the outcomes are processed using a classical computer. We prove that, in various tasks, quantum machines can learn from exponentially fewer experiments than those required in conventional experiments. The exponential advantage holds in predicting properties of physical systems, performing quantum principal component analysis on noisy states, and learning approximate models of physical dynamics. In some tasks, the quantum processing needed to achieve the exponential advantage can be modest; for example, one can simultaneously learn about many noncommuting observables by processing only two copies of the system. Conducting experiments with up to 40 superconducting qubits and 1300 quantum gates, we demonstrate that a substantial quantum advantage can be realized using today's relatively noisy quantum processors. Our results highlight how quantum technology can enable powerful new strategies to learn about nature.

Variational Quantum Algorithms

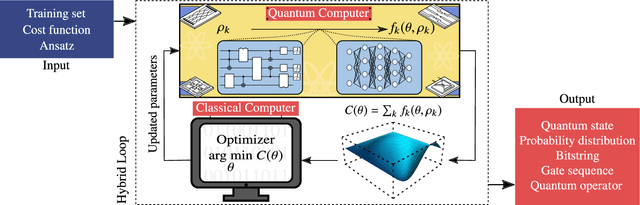
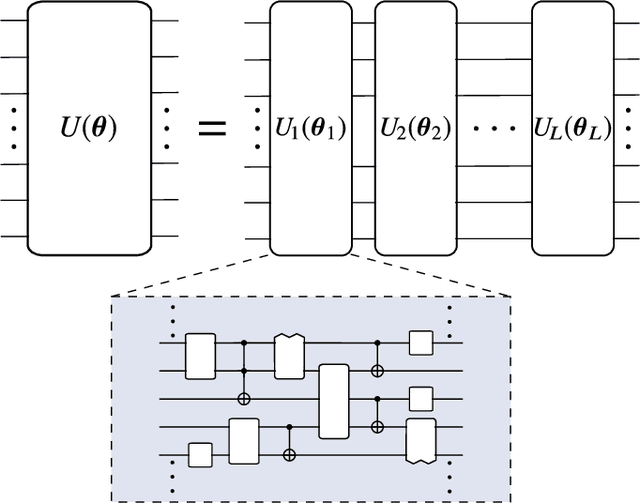
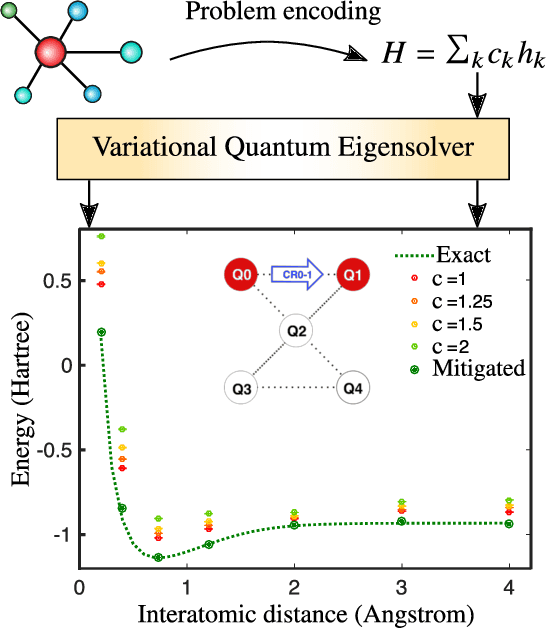
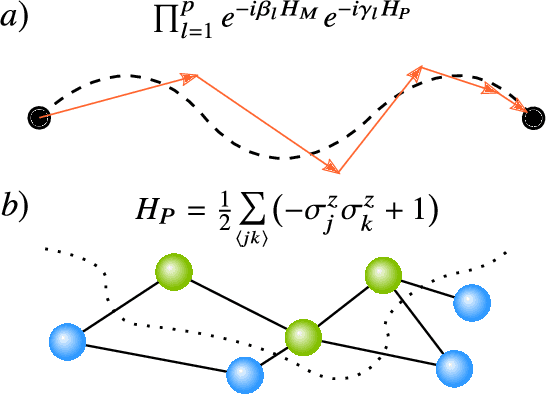
Applications such as simulating large quantum systems or solving large-scale linear algebra problems are immensely challenging for classical computers due their extremely high computational cost. Quantum computers promise to unlock these applications, although fault-tolerant quantum computers will likely not be available for several years. Currently available quantum devices have serious constraints, including limited qubit numbers and noise processes that limit circuit depth. Variational Quantum Algorithms (VQAs), which employ a classical optimizer to train a parametrized quantum circuit, have emerged as a leading strategy to address these constraints. VQAs have now been proposed for essentially all applications that researchers have envisioned for quantum computers, and they appear to the best hope for obtaining quantum advantage. Nevertheless, challenges remain including the trainability, accuracy, and efficiency of VQAs. In this review article we present an overview of the field of VQAs. Furthermore, we discuss strategies to overcome their challenges as well as the exciting prospects for using them as a means to obtain quantum advantage.

Power of data in quantum machine learning

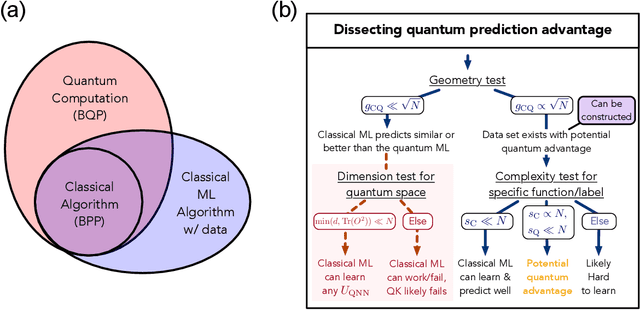
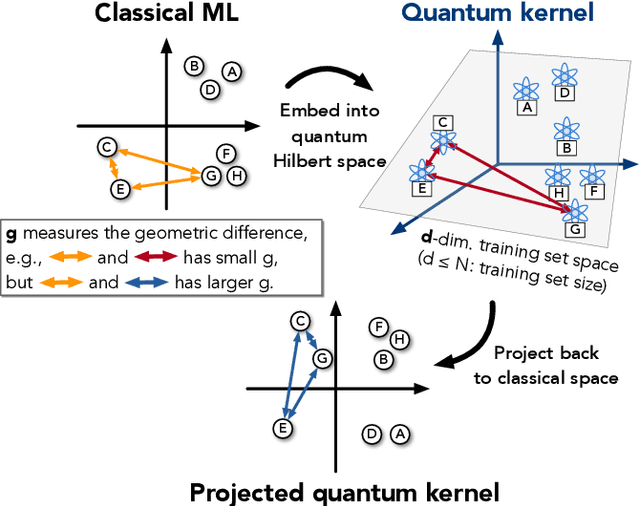
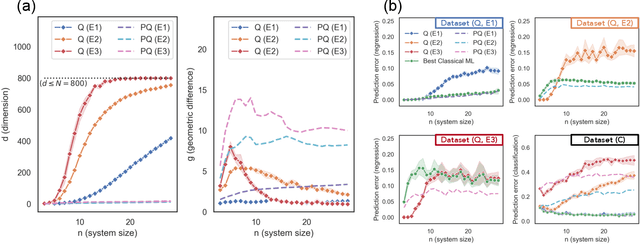
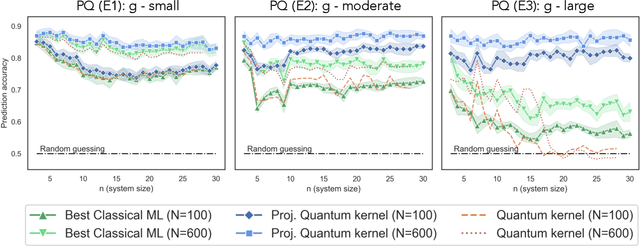
The use of quantum computing for machine learning is among the most exciting prospective applications of quantum technologies. At the crux of excitement is the potential for quantum computers to perform some computations exponentially faster than their classical counterparts. However, a machine learning task where some data is provided can be considerably different than more commonly studied computational tasks. In this work, we show that some problems that are classically hard to compute can be predicted easily with classical machines that learn from data. We find that classical machines can often compete or outperform existing quantum models even on data sets generated by quantum evolution, especially at large system sizes. Using rigorous prediction error bounds as a foundation, we develop a methodology for assessing the potential for quantum advantage in prediction on learning tasks. We show how the use of exponentially large quantum Hilbert space in existing quantum models can result in significantly inferior prediction performance compared to classical machines. To circumvent the observed setbacks, we propose an improvement by projecting all quantum states to an approximate classical representation. The projected quantum model provides a simple and rigorous quantum speed-up for a recently proposed learning problem in the fault-tolerant regime. For more near-term quantum models, the projected versions demonstrate a significant prediction advantage over some classical models on engineered data sets in one of the largest numerical tests for gate-based quantum machine learning to date, up to 30 qubits.

Learning to learn with quantum neural networks via classical neural networks

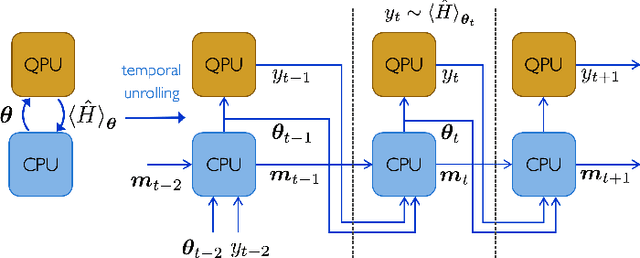
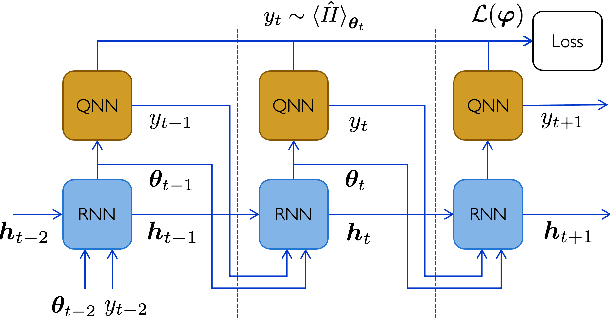
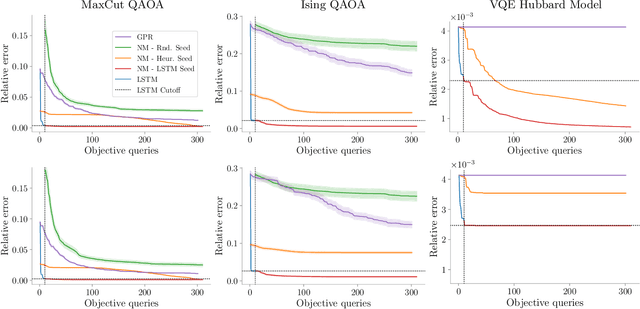
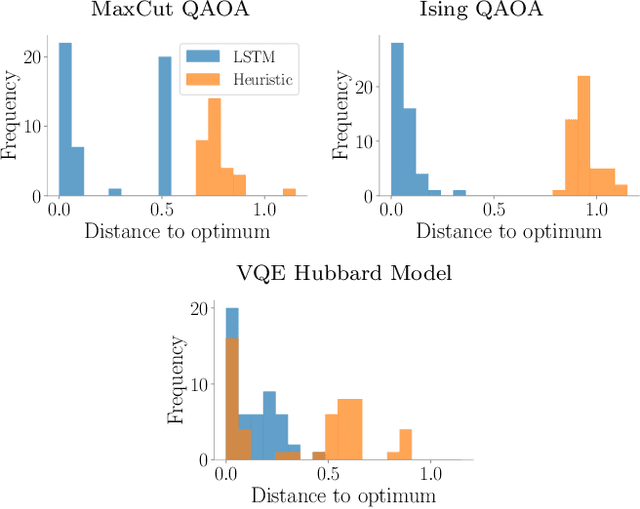
Quantum Neural Networks (QNNs) are a promising variational learning paradigm with applications to near-term quantum processors, however they still face some significant challenges. One such challenge is finding good parameter initialization heuristics that ensure rapid and consistent convergence to local minima of the parameterized quantum circuit landscape. In this work, we train classical neural networks to assist in the quantum learning process, also know as meta-learning, to rapidly find approximate optima in the parameter landscape for several classes of quantum variational algorithms. Specifically, we train classical recurrent neural networks to find approximately optimal parameters within a small number of queries of the cost function for the Quantum Approximate Optimization Algorithm (QAOA) for MaxCut, QAOA for Sherrington-Kirkpatrick Ising model, and for a Variational Quantum Eigensolver for the Hubbard model. By initializing other optimizers at parameter values suggested by the classical neural network, we demonstrate a significant improvement in the total number of optimization iterations required to reach a given accuracy. We further demonstrate that the optimization strategies learned by the neural network generalize well across a range of problem instance sizes. This opens up the possibility of training on small, classically simulatable problem instances, in order to initialize larger, classically intractably simulatable problem instances on quantum devices, thereby significantly reducing the number of required quantum-classical optimization iterations.

Barren plateaus in quantum neural network training landscapes

Many experimental proposals for noisy intermediate scale quantum devices involve training a parameterized quantum circuit with a classical optimization loop. Such hybrid quantum-classical algorithms are popular for applications in quantum simulation, optimization, and machine learning. Due to its simplicity and hardware efficiency, random circuits are often proposed as initial guesses for exploring the space of quantum states. We show that the exponential dimension of Hilbert space and the gradient estimation complexity make this choice unsuitable for hybrid quantum-classical algorithms run on more than a few qubits. Specifically, we show that for a wide class of reasonable parameterized quantum circuits, the probability that the gradient along any reasonable direction is non-zero to some fixed precision is exponentially small as a function of the number of qubits. We argue that this is related to the 2-design characteristic of random circuits, and that solutions to this problem must be studied.

Bayesian Network Structure Learning Using Quantum Annealing

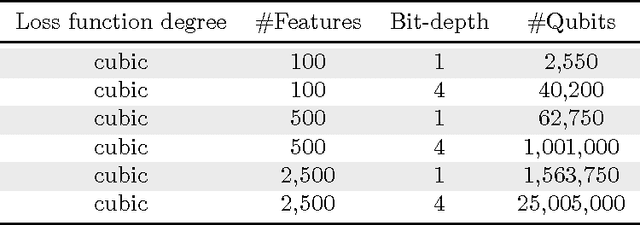
We introduce a method for the problem of learning the structure of a Bayesian network using the quantum adiabatic algorithm. We do so by introducing an efficient reformulation of a standard posterior-probability scoring function on graphs as a pseudo-Boolean function, which is equivalent to a system of 2-body Ising spins, as well as suitable penalty terms for enforcing the constraints necessary for the reformulation; our proposed method requires $\mathcal O(n^2)$ qubits for $n$ Bayesian network variables. Furthermore, we prove lower bounds on the necessary weighting of these penalty terms. The logical structure resulting from the mapping has the appealing property that it is instance-independent for a given number of Bayesian network variables, as well as being independent of the number of data cases.

Construction of non-convex polynomial loss functions for training a binary classifier with quantum annealing

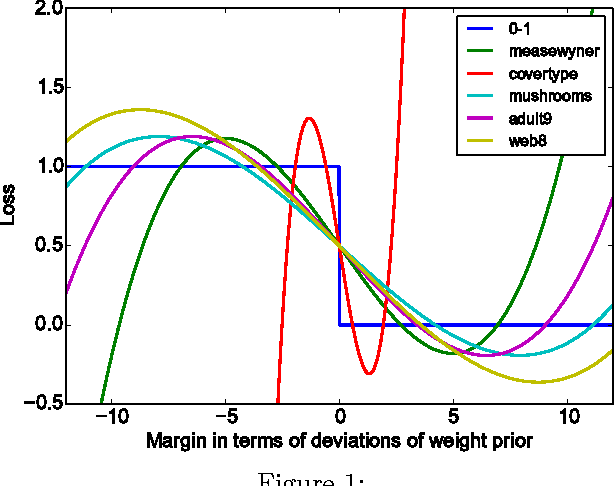
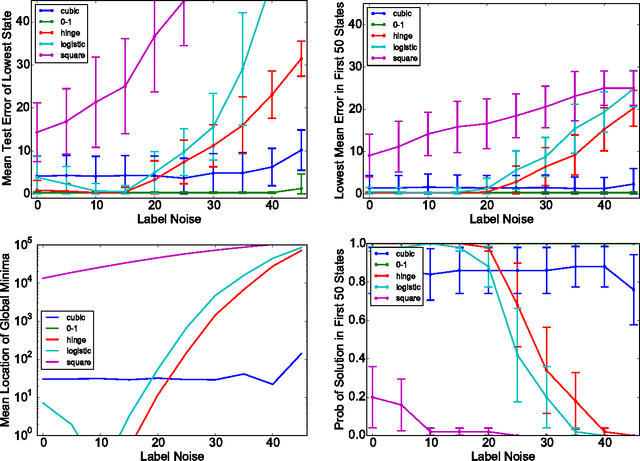
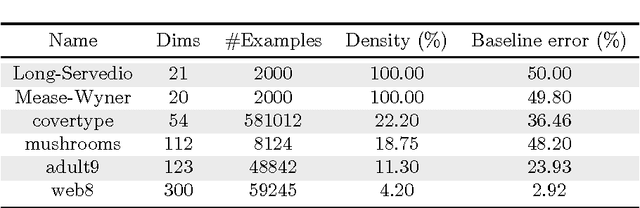
Quantum annealing is a heuristic quantum algorithm which exploits quantum resources to minimize an objective function embedded as the energy levels of a programmable physical system. To take advantage of a potential quantum advantage, one needs to be able to map the problem of interest to the native hardware with reasonably low overhead. Because experimental considerations constrain our objective function to take the form of a low degree PUBO (polynomial unconstrained binary optimization), we employ non-convex loss functions which are polynomial functions of the margin. We show that these loss functions are robust to label noise and provide a clear advantage over convex methods. These loss functions may also be useful for classical approaches as they compile to regularized risk expressions which can be evaluated in constant time with respect to the number of training examples.