Summit Vitals: Multi-Camera and Multi-Signal Biosensing at High Altitudes

Video photoplethysmography (vPPG) is an emerging method for non-invasive and convenient measurement of physiological signals, utilizing two primary approaches: remote video PPG (rPPG) and contact video PPG (cPPG). Monitoring vitals in high-altitude environments, where heart rates tend to increase and blood oxygen levels often decrease, presents significant challenges. To address these issues, we introduce the SUMS dataset comprising 80 synchronized non-contact facial and contact finger videos from 10 subjects during exercise and oxygen recovery scenarios, capturing PPG, respiration rate (RR), and SpO2. This dataset is designed to validate video vitals estimation algorithms and compare facial rPPG with finger cPPG. Additionally, fusing videos from different positions (i.e., face and finger) reduces the mean absolute error (MAE) of SpO2 predictions by 7.6\% and 10.6\% compared to only face and only finger, respectively. In cross-subject evaluation, we achieve an MAE of less than 0.5 BPM for HR estimation and 2.5\% for SpO2 estimation, demonstrating the precision of our multi-camera fusion techniques. Our findings suggest that simultaneous training on multiple indicators, such as PPG and blood oxygen, can reduce MAE in SpO2 estimation by 17.8\%.

Emergence and Causality in Complex Systems: A Survey on Causal Emergence and Related Quantitative Studies

Emergence and causality are two fundamental concepts for understanding complex systems. They are interconnected. On one hand, emergence refers to the phenomenon where macroscopic properties cannot be solely attributed to the cause of individual properties. On the other hand, causality can exhibit emergence, meaning that new causal laws may arise as we increase the level of abstraction. Causal emergence theory aims to bridge these two concepts and even employs measures of causality to quantify emergence. This paper provides a comprehensive review of recent advancements in quantitative theories and applications of causal emergence. Two key problems are addressed: quantifying causal emergence and identifying it in data. Addressing the latter requires the use of machine learning techniques, thus establishing a connection between causal emergence and artificial intelligence. We highlighted that the architectures used for identifying causal emergence are shared by causal representation learning, causal model abstraction, and world model-based reinforcement learning. Consequently, progress in any of these areas can benefit the others. Potential applications and future perspectives are also discussed in the final section of the review.

Learning to learn with quantum neural networks via classical neural networks

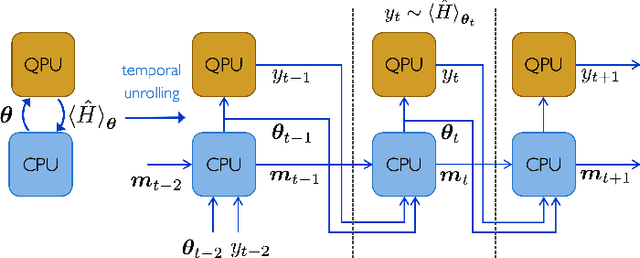
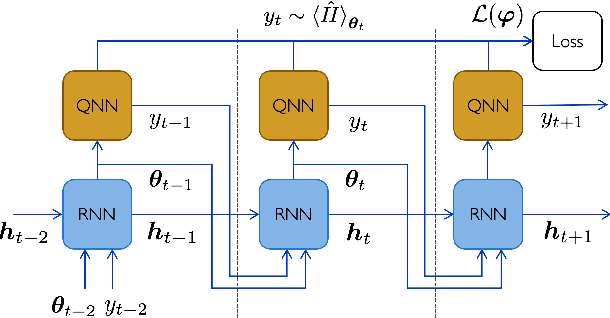
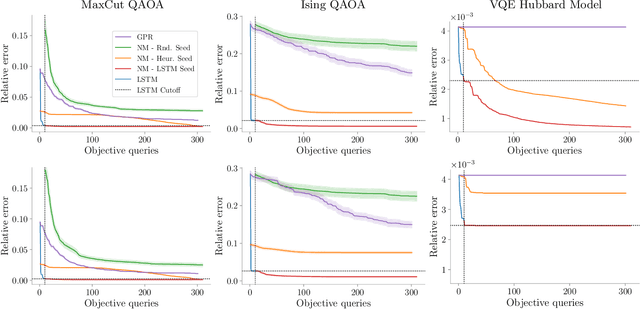
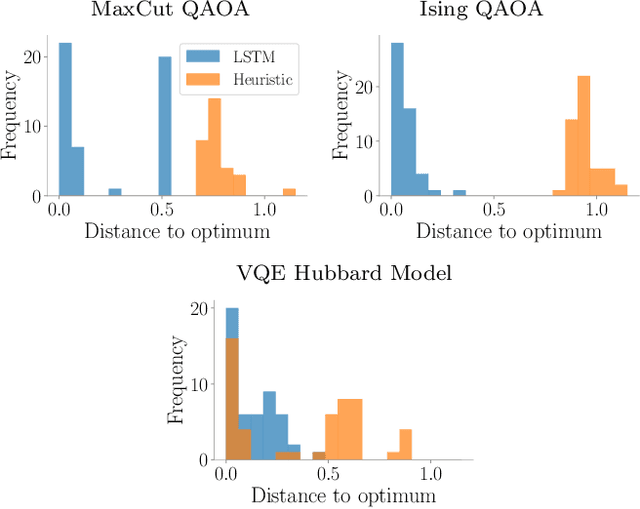
Quantum Neural Networks (QNNs) are a promising variational learning paradigm with applications to near-term quantum processors, however they still face some significant challenges. One such challenge is finding good parameter initialization heuristics that ensure rapid and consistent convergence to local minima of the parameterized quantum circuit landscape. In this work, we train classical neural networks to assist in the quantum learning process, also know as meta-learning, to rapidly find approximate optima in the parameter landscape for several classes of quantum variational algorithms. Specifically, we train classical recurrent neural networks to find approximately optimal parameters within a small number of queries of the cost function for the Quantum Approximate Optimization Algorithm (QAOA) for MaxCut, QAOA for Sherrington-Kirkpatrick Ising model, and for a Variational Quantum Eigensolver for the Hubbard model. By initializing other optimizers at parameter values suggested by the classical neural network, we demonstrate a significant improvement in the total number of optimization iterations required to reach a given accuracy. We further demonstrate that the optimization strategies learned by the neural network generalize well across a range of problem instance sizes. This opens up the possibility of training on small, classically simulatable problem instances, in order to initialize larger, classically intractably simulatable problem instances on quantum devices, thereby significantly reducing the number of required quantum-classical optimization iterations.