Emergence and Causality in Complex Systems: A Survey on Causal Emergence and Related Quantitative Studies

Emergence and causality are two fundamental concepts for understanding complex systems. They are interconnected. On one hand, emergence refers to the phenomenon where macroscopic properties cannot be solely attributed to the cause of individual properties. On the other hand, causality can exhibit emergence, meaning that new causal laws may arise as we increase the level of abstraction. Causal emergence theory aims to bridge these two concepts and even employs measures of causality to quantify emergence. This paper provides a comprehensive review of recent advancements in quantitative theories and applications of causal emergence. Two key problems are addressed: quantifying causal emergence and identifying it in data. Addressing the latter requires the use of machine learning techniques, thus establishing a connection between causal emergence and artificial intelligence. We highlighted that the architectures used for identifying causal emergence are shared by causal representation learning, causal model abstraction, and world model-based reinforcement learning. Consequently, progress in any of these areas can benefit the others. Potential applications and future perspectives are also discussed in the final section of the review.

Gumbel-softmax-based Optimization: A Simple General Framework for Optimization Problems on Graphs

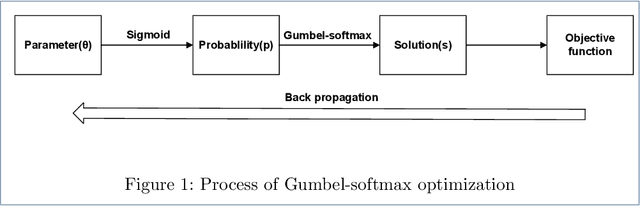
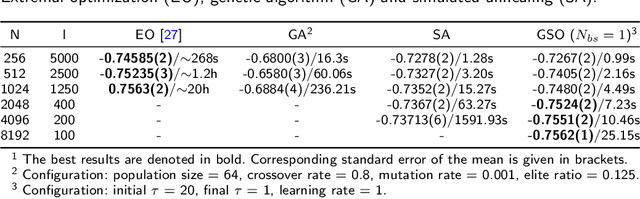
In computer science, there exist a large number of optimization problems defined on graphs, that is to find a best node state configuration or a network structure such that the designed objective function is optimized under some constraints. However, these problems are notorious for their hardness to solve because most of them are NP-hard or NP-complete. Although traditional general methods such as simulated annealing (SA), genetic algorithms (GA) and so forth have been devised to these hard problems, their accuracy and time consumption are not satisfying in practice. In this work, we proposed a simple, fast, and general algorithm framework based on advanced automatic differentiation technique empowered by deep learning frameworks. By introducing Gumbel-softmax technique, we can optimize the objective function directly by gradient descent algorithm regardless of the discrete nature of variables. We also introduce evolution strategy to parallel version of our algorithm. We test our algorithm on three representative optimization problems on graph including modularity optimization from network science, Sherrington-Kirkpatrick (SK) model from statistical physics, maximum independent set (MIS) and minimum vertex cover (MVC) problem from combinatorial optimization on graph. High-quality solutions can be obtained with much less time consuming compared to traditional approaches.