Guozheng Lin
Gumbel-softmax-based Optimization: A Simple General Framework for Optimization Problems on Graphs
Apr 14, 2020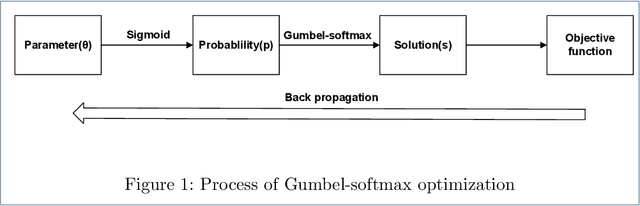


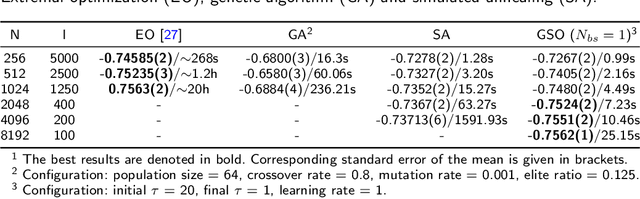
Abstract:In computer science, there exist a large number of optimization problems defined on graphs, that is to find a best node state configuration or a network structure such that the designed objective function is optimized under some constraints. However, these problems are notorious for their hardness to solve because most of them are NP-hard or NP-complete. Although traditional general methods such as simulated annealing (SA), genetic algorithms (GA) and so forth have been devised to these hard problems, their accuracy and time consumption are not satisfying in practice. In this work, we proposed a simple, fast, and general algorithm framework based on advanced automatic differentiation technique empowered by deep learning frameworks. By introducing Gumbel-softmax technique, we can optimize the objective function directly by gradient descent algorithm regardless of the discrete nature of variables. We also introduce evolution strategy to parallel version of our algorithm. We test our algorithm on three representative optimization problems on graph including modularity optimization from network science, Sherrington-Kirkpatrick (SK) model from statistical physics, maximum independent set (MIS) and minimum vertex cover (MVC) problem from combinatorial optimization on graph. High-quality solutions can be obtained with much less time consuming compared to traditional approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge