CGCOD: Class-Guided Camouflaged Object Detection

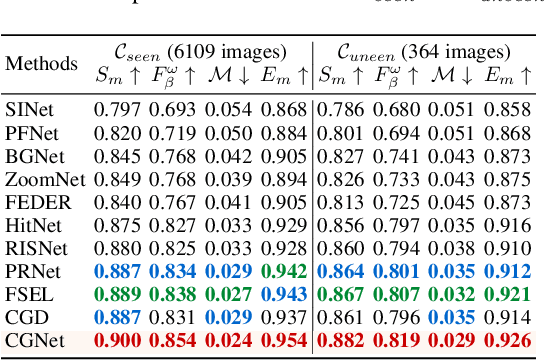
Camouflaged Object Detection (COD) is designed to identify objects that blend seamlessly with their surroundings. Due to the complexity of camouflaged objects (such as shape, color, and texture), their semantic cues are often blurred or completely lost, posing a significant challenge for COD. Existing COD methods often rely on visual features, which are not stable enough in changeable camouflage environments. This instability leads to false positives and false negatives, resulting in incomplete or inaccurate segmentation results. In this paper, to solve this problem, we propose a new task, Class-Guided Camouflaged Object Detection (CG-COD), which extends the traditional COD task by introducing object class knowledge, significantly improving the robustness and segmentation accuracy of the model in complex environments. Toward this end, we construct a dataset, CamoClass, containing the camouflaged objects in the real scenes and their corresponding class annotation. Based on this, we propose a multi-stage framework CGNet which consists of a plug-and-play class prompt generator and a class-guided detector. Under the guidance of textual information, CGNet enables efficient segmentation. It is worth emphasizing that for the first time, we extend the object class annotations on existing COD benchmark datasets, and introduce a flexible framework to improve the performance of the existing COD model under text guidance.

Benign Overfitting in Out-of-Distribution Generalization of Linear Models

Benign overfitting refers to the phenomenon where an over-parameterized model fits the training data perfectly, including noise in the data, but still generalizes well to the unseen test data. While prior work provides some theoretical understanding of this phenomenon under the in-distribution setup, modern machine learning often operates in a more challenging Out-of-Distribution (OOD) regime, where the target (test) distribution can be rather different from the source (training) distribution. In this work, we take an initial step towards understanding benign overfitting in the OOD regime by focusing on the basic setup of over-parameterized linear models under covariate shift. We provide non-asymptotic guarantees proving that benign overfitting occurs in standard ridge regression, even under the OOD regime when the target covariance satisfies certain structural conditions. We identify several vital quantities relating to source and target covariance, which govern the performance of OOD generalization. Our result is sharp, which provably recovers prior in-distribution benign overfitting guarantee [Tsigler and Bartlett, 2023], as well as under-parameterized OOD guarantee [Ge et al., 2024] when specializing to each setup. Moreover, we also present theoretical results for a more general family of target covariance matrix, where standard ridge regression only achieves a slow statistical rate of $O(1/\sqrt{n})$ for the excess risk, while Principal Component Regression (PCR) is guaranteed to achieve the fast rate $O(1/n)$, where $n$ is the number of samples.

Topology-Aware Dynamic Reweighting for Distribution Shifts on Graph

Graph Neural Networks (GNNs) are widely used for node classification tasks but often fail to generalize when training and test nodes come from different distributions, limiting their practicality. To overcome this, recent approaches adopt invariant learning techniques from the out-of-distribution (OOD) generalization field, which seek to establish stable prediction methods across environments. However, the applicability of these invariant assumptions to graph data remains unverified, and such methods often lack solid theoretical support. In this work, we introduce the Topology-Aware Dynamic Reweighting (TAR) framework, which dynamically adjusts sample weights through gradient flow in the geometric Wasserstein space during training. Instead of relying on strict invariance assumptions, we prove that our method is able to provide distributional robustness, thereby enhancing the out-of-distribution generalization performance on graph data. By leveraging the inherent graph structure, TAR effectively addresses distribution shifts. Our framework's superiority is demonstrated through standard testing on four graph OOD datasets and three class-imbalanced node classification datasets, exhibiting marked improvements over existing methods.

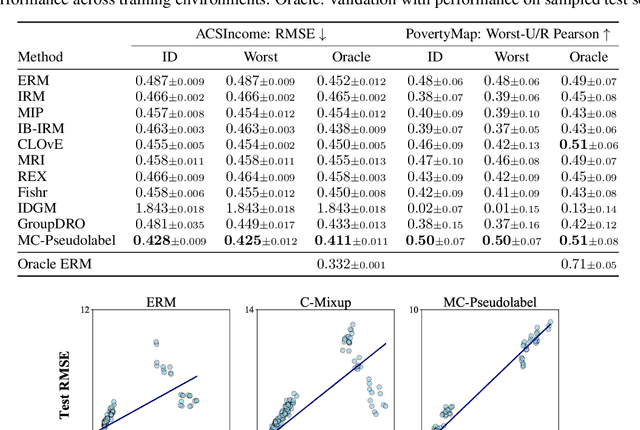
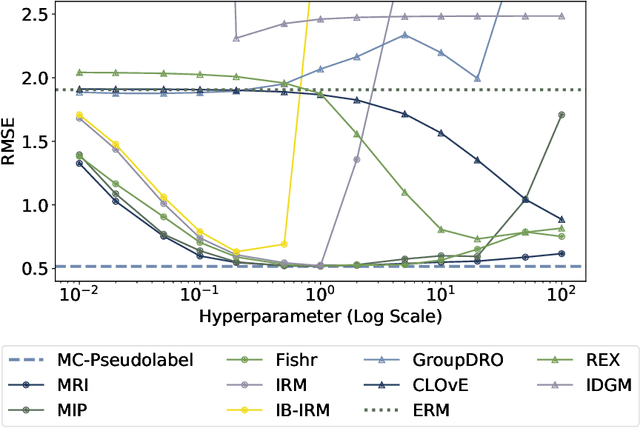
Bridging Multicalibration and Out-of-distribution Generalization Beyond Covariate Shift

We establish a new model-agnostic optimization framework for out-of-distribution generalization via multicalibration, a criterion that ensures a predictor is calibrated across a family of overlapping groups. Multicalibration is shown to be associated with robustness of statistical inference under covariate shift. We further establish a link between multicalibration and robustness for prediction tasks both under and beyond covariate shift. We accomplish this by extending multicalibration to incorporate grouping functions that consider covariates and labels jointly. This leads to an equivalence of the extended multicalibration and invariance, an objective for robust learning in existence of concept shift. We show a linear structure of the grouping function class spanned by density ratios, resulting in a unifying framework for robust learning by designing specific grouping functions. We propose MC-Pseudolabel, a post-processing algorithm to achieve both extended multicalibration and out-of-distribution generalization. The algorithm, with lightweight hyperparameters and optimization through a series of supervised regression steps, achieves superior performance on real-world datasets with distribution shift.

A Survey on Evaluation of Out-of-Distribution Generalization

Machine learning models, while progressively advanced, rely heavily on the IID assumption, which is often unfulfilled in practice due to inevitable distribution shifts. This renders them susceptible and untrustworthy for deployment in risk-sensitive applications. Such a significant problem has consequently spawned various branches of works dedicated to developing algorithms capable of Out-of-Distribution (OOD) generalization. Despite these efforts, much less attention has been paid to the evaluation of OOD generalization, which is also a complex and fundamental problem. Its goal is not only to assess whether a model's OOD generalization capability is strong or not, but also to evaluate where a model generalizes well or poorly. This entails characterizing the types of distribution shifts that a model can effectively address, and identifying the safe and risky input regions given a model. This paper serves as the first effort to conduct a comprehensive review of OOD evaluation. We categorize existing research into three paradigms: OOD performance testing, OOD performance prediction, and OOD intrinsic property characterization, according to the availability of test data. Additionally, we briefly discuss OOD evaluation in the context of pretrained models. In closing, we propose several promising directions for future research in OOD evaluation.

Emergence and Causality in Complex Systems: A Survey on Causal Emergence and Related Quantitative Studies

Emergence and causality are two fundamental concepts for understanding complex systems. They are interconnected. On one hand, emergence refers to the phenomenon where macroscopic properties cannot be solely attributed to the cause of individual properties. On the other hand, causality can exhibit emergence, meaning that new causal laws may arise as we increase the level of abstraction. Causal emergence theory aims to bridge these two concepts and even employs measures of causality to quantify emergence. This paper provides a comprehensive review of recent advancements in quantitative theories and applications of causal emergence. Two key problems are addressed: quantifying causal emergence and identifying it in data. Addressing the latter requires the use of machine learning techniques, thus establishing a connection between causal emergence and artificial intelligence. We highlighted that the architectures used for identifying causal emergence are shared by causal representation learning, causal model abstraction, and world model-based reinforcement learning. Consequently, progress in any of these areas can benefit the others. Potential applications and future perspectives are also discussed in the final section of the review.

Geometry-Calibrated DRO: Combating Over-Pessimism with Free Energy Implications

Machine learning algorithms minimizing average risk are susceptible to distributional shifts. Distributionally Robust Optimization (DRO) addresses this issue by optimizing the worst-case risk within an uncertainty set. However, DRO suffers from over-pessimism, leading to low-confidence predictions, poor parameter estimations as well as poor generalization. In this work, we conduct a theoretical analysis of a probable root cause of over-pessimism: excessive focus on noisy samples. To alleviate the impact of noise, we incorporate data geometry into calibration terms in DRO, resulting in our novel Geometry-Calibrated DRO (GCDRO) for regression. We establish the connection between our risk objective and the Helmholtz free energy in statistical physics, and this free-energy-based risk can extend to standard DRO methods. Leveraging gradient flow in Wasserstein space, we develop an approximate minimax optimization algorithm with a bounded error ratio and elucidate how our approach mitigates noisy sample effects. Comprehensive experiments confirm GCDRO's superiority over conventional DRO methods.

Transforming Graphs for Enhanced Attribute-Based Clustering: An Innovative Graph Transformer Method

Graph Representation Learning (GRL) is an influential methodology, enabling a more profound understanding of graph-structured data and aiding graph clustering, a critical task across various domains. The recent incursion of attention mechanisms, originally an artifact of Natural Language Processing (NLP), into the realm of graph learning has spearheaded a notable shift in research trends. Consequently, Graph Attention Networks (GATs) and Graph Attention Auto-Encoders have emerged as preferred tools for graph clustering tasks. Yet, these methods primarily employ a local attention mechanism, thereby curbing their capacity to apprehend the intricate global dependencies between nodes within graphs. Addressing these impediments, this study introduces an innovative method known as the Graph Transformer Auto-Encoder for Graph Clustering (GTAGC). By melding the Graph Auto-Encoder with the Graph Transformer, GTAGC is adept at capturing global dependencies between nodes. This integration amplifies the graph representation and surmounts the constraints posed by the local attention mechanism. The architecture of GTAGC encompasses graph embedding, integration of the Graph Transformer within the autoencoder structure, and a clustering component. It strategically alternates between graph embedding and clustering, thereby tailoring the Graph Transformer for clustering tasks, whilst preserving the graph's global structural information. Through extensive experimentation on diverse benchmark datasets, GTAGC has exhibited superior performance against existing state-of-the-art graph clustering methodologies. This pioneering approach represents a novel contribution to the field of graph clustering, paving the way for promising avenues in future research.

Predictive Heterogeneity: Measures and Applications

As an intrinsic and fundamental property of big data, data heterogeneity exists in a variety of real-world applications, such as precision medicine, autonomous driving, financial applications, etc. For machine learning algorithms, the ignorance of data heterogeneity will greatly hurt the generalization performance and the algorithmic fairness, since the prediction mechanisms among different sub-populations are likely to differ from each other. In this work, we focus on the data heterogeneity that affects the prediction of machine learning models, and firstly propose the \emph{usable predictive heterogeneity}, which takes into account the model capacity and computational constraints. We prove that it can be reliably estimated from finite data with probably approximately correct (PAC) bounds. Additionally, we design a bi-level optimization algorithm to explore the usable predictive heterogeneity from data. Empirically, the explored heterogeneity provides insights for sub-population divisions in income prediction, crop yield prediction and image classification tasks, and leveraging such heterogeneity benefits the out-of-distribution generalization performance.

Significant Ties Graph Neural Networks for Continuous-Time Temporal Networks Modeling

Temporal networks are suitable for modeling complex evolving systems. It has a wide range of applications, such as social network analysis, recommender systems, and epidemiology. Recently, modeling such dynamic systems has drawn great attention in many domains. However, most existing approaches resort to taking discrete snapshots of the temporal networks and modeling all events with equal importance. This paper proposes Significant Ties Graph Neural Networks (STGNN), a novel framework that captures and describes significant ties. To better model the diversity of interactions, STGNN introduces a novel aggregation mechanism to organize the most significant historical neighbors' information and adaptively obtain the significance of node pairs. Experimental results on four real networks demonstrate the effectiveness of the proposed framework.