Dimension-Free Decision Calibration for Nonlinear Loss Functions

When model predictions inform downstream decision making, a natural question is under what conditions can the decision-makers simply respond to the predictions as if they were the true outcomes. Calibration suffices to guarantee that simple best-response to predictions is optimal. However, calibration for high-dimensional prediction outcome spaces requires exponential computational and statistical complexity. The recent relaxation known as decision calibration ensures the optimality of the simple best-response rule while requiring only polynomial sample complexity in the dimension of outcomes. However, known results on calibration and decision calibration crucially rely on linear loss functions for establishing best-response optimality. A natural approach to handle nonlinear losses is to map outcomes $y$ into a feature space $\phi(y)$ of dimension $m$, then approximate losses with linear functions of $\phi(y)$. Unfortunately, even simple classes of nonlinear functions can demand exponentially large or infinite feature dimensions $m$. A key open problem is whether it is possible to achieve decision calibration with sample complexity independent of~$m$. We begin with a negative result: even verifying decision calibration under standard deterministic best response inherently requires sample complexity polynomial in~$m$. Motivated by this lower bound, we investigate a smooth version of decision calibration in which decision-makers follow a smooth best-response. This smooth relaxation enables dimension-free decision calibration algorithms. We introduce algorithms that, given $\mathrm{poly}(|A|,1/\epsilon)$ samples and any initial predictor~$p$, can efficiently post-process it to satisfy decision calibration without worsening accuracy. Our algorithms apply broadly to function classes that can be well-approximated by bounded-norm functions in (possibly infinite-dimensional) separable RKHS.

Multi-Agent Imitation Learning: Value is Easy, Regret is Hard

We study a multi-agent imitation learning (MAIL) problem where we take the perspective of a learner attempting to coordinate a group of agents based on demonstrations of an expert doing so. Most prior work in MAIL essentially reduces the problem to matching the behavior of the expert within the support of the demonstrations. While doing so is sufficient to drive the value gap between the learner and the expert to zero under the assumption that agents are non-strategic, it does not guarantee robustness to deviations by strategic agents. Intuitively, this is because strategic deviations can depend on a counterfactual quantity: the coordinator's recommendations outside of the state distribution their recommendations induce. In response, we initiate the study of an alternative objective for MAIL in Markov Games we term the regret gap that explicitly accounts for potential deviations by agents in the group. We first perform an in-depth exploration of the relationship between the value and regret gaps. First, we show that while the value gap can be efficiently minimized via a direct extension of single-agent IL algorithms, even value equivalence can lead to an arbitrarily large regret gap. This implies that achieving regret equivalence is harder than achieving value equivalence in MAIL. We then provide a pair of efficient reductions to no-regret online convex optimization that are capable of minimizing the regret gap (a) under a coverage assumption on the expert (MALICE) or (b) with access to a queryable expert (BLADES).

Generating Private Synthetic Data with Genetic Algorithms

We study the problem of efficiently generating differentially private synthetic data that approximate the statistical properties of an underlying sensitive dataset. In recent years, there has been a growing line of work that approaches this problem using first-order optimization techniques. However, such techniques are restricted to optimizing differentiable objectives only, severely limiting the types of analyses that can be conducted. For example, first-order mechanisms have been primarily successful in approximating statistical queries only in the form of marginals for discrete data domains. In some cases, one can circumvent such issues by relaxing the task's objective to maintain differentiability. However, even when possible, these approaches impose a fundamental limitation in which modifications to the minimization problem become additional sources of error. Therefore, we propose Private-GSD, a private genetic algorithm based on zeroth-order optimization heuristics that do not require modifying the original objective. As a result, it avoids the aforementioned limitations of first-order optimization. We empirically evaluate Private-GSD against baseline algorithms on data derived from the American Community Survey across a variety of statistics--otherwise known as statistical queries--both for discrete and real-valued attributes. We show that Private-GSD outperforms the state-of-the-art methods on non-differential queries while matching accuracy in approximating differentiable ones.

A Context-Integrated Transformer-Based Neural Network for Auction Design

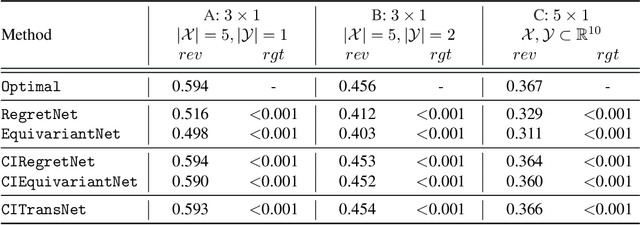
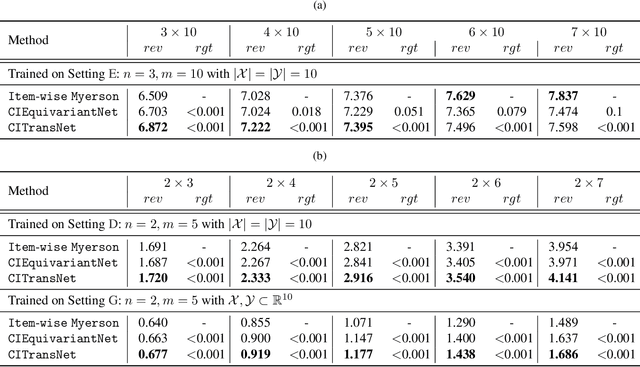
One of the central problems in auction design is developing an incentive-compatible mechanism that maximizes the auctioneer's expected revenue. While theoretical approaches have encountered bottlenecks in multi-item auctions, recently, there has been much progress on finding the optimal mechanism through deep learning. However, these works either focus on a fixed set of bidders and items, or restrict the auction to be symmetric. In this work, we overcome such limitations by factoring \emph{public} contextual information of bidders and items into the auction learning framework. We propose $\mathtt{CITransNet}$, a context-integrated transformer-based neural network for optimal auction design, which maintains permutation-equivariance over bids and contexts while being able to find asymmetric solutions. We show by extensive experiments that $\mathtt{CITransNet}$ can recover the known optimal solutions in single-item settings, outperform strong baselines in multi-item auctions, and generalize well to cases other than those in training.