Bridging Multicalibration and Out-of-distribution Generalization Beyond Covariate Shift
Paper and Code
Jun 02, 2024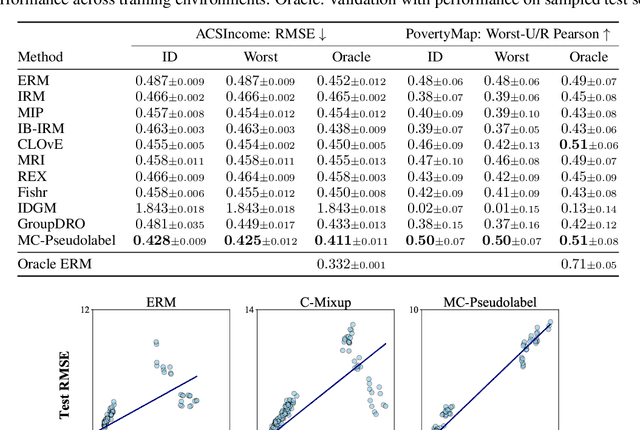

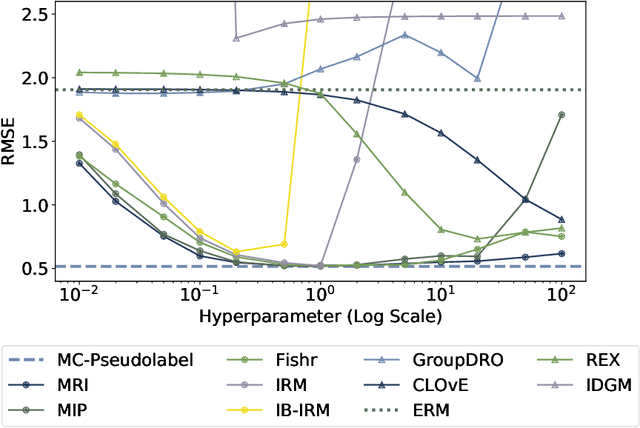
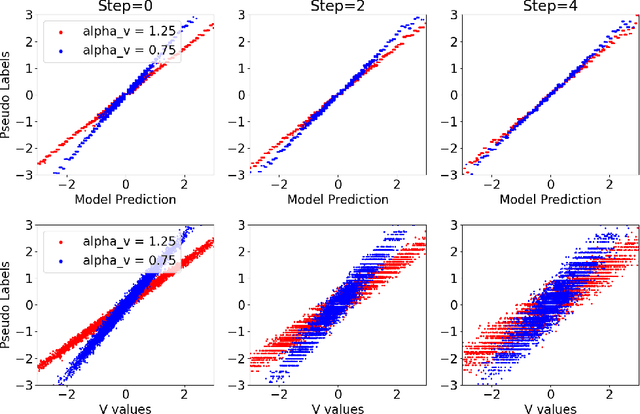
We establish a new model-agnostic optimization framework for out-of-distribution generalization via multicalibration, a criterion that ensures a predictor is calibrated across a family of overlapping groups. Multicalibration is shown to be associated with robustness of statistical inference under covariate shift. We further establish a link between multicalibration and robustness for prediction tasks both under and beyond covariate shift. We accomplish this by extending multicalibration to incorporate grouping functions that consider covariates and labels jointly. This leads to an equivalence of the extended multicalibration and invariance, an objective for robust learning in existence of concept shift. We show a linear structure of the grouping function class spanned by density ratios, resulting in a unifying framework for robust learning by designing specific grouping functions. We propose MC-Pseudolabel, a post-processing algorithm to achieve both extended multicalibration and out-of-distribution generalization. The algorithm, with lightweight hyperparameters and optimization through a series of supervised regression steps, achieves superior performance on real-world datasets with distribution shift.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge