QuestA: Expanding Reasoning Capacity in LLMs via Question Augmentation

Reinforcement learning (RL) has become a key component in training large language reasoning models (LLMs). However, recent studies questions its effectiveness in improving multi-step reasoning-particularly on hard problems. To address this challenge, we propose a simple yet effective strategy via Question Augmentation: introduce partial solutions during training to reduce problem difficulty and provide more informative learning signals. Our method, QuestA, when applied during RL training on math reasoning tasks, not only improves pass@1 but also pass@k-particularly on problems where standard RL struggles to make progress. This enables continual improvement over strong open-source models such as DeepScaleR and OpenMath Nemotron, further enhancing their reasoning capabilities. We achieve new state-of-the-art results on math benchmarks using 1.5B-parameter models: 67.1% (+5.3%) on AIME24, 59.5% (+10.0%) on AIME25, and 35.5% (+4.0%) on HMMT25. Further, we provide theoretical explanations that QuestA improves sample efficiency, offering a practical and generalizable pathway for expanding reasoning capability through RL.

Ineq-Comp: Benchmarking Human-Intuitive Compositional Reasoning in Automated Theorem Proving on Inequalities

LLM-based formal proof assistants (e.g., in Lean) hold great promise for automating mathematical discovery. But beyond syntactic correctness, do these systems truly understand mathematical structure as humans do? We investigate this question through the lens of mathematical inequalities -- a fundamental tool across many domains. While modern provers can solve basic inequalities, we probe their ability to handle human-intuitive compositionality. We introduce Ineq-Comp, a benchmark built from elementary inequalities through systematic transformations, including variable duplication, algebraic rewriting, and multi-step composition. Although these problems remain easy for humans, we find that most provers -- including Goedel, STP, and Kimina-7B -- struggle significantly. DeepSeek-Prover-V2-7B shows relative robustness -- possibly because it is trained to decompose the problems into sub-problems -- but still suffers a 20\% performance drop (pass@32). Strikingly, performance remains poor for all models even when formal proofs of the constituent parts are provided in context, revealing that the source of weakness is indeed in compositional reasoning. Our results expose a persisting gap between the generalization behavior of current AI provers and human mathematical intuition.

Task Generalization With AutoRegressive Compositional Structure: Can Learning From $\d$ Tasks Generalize to $\d^{T}$ Tasks?

Large language models (LLMs) exhibit remarkable task generalization, solving tasks they were never explicitly trained on with only a few demonstrations. This raises a fundamental question: When can learning from a small set of tasks generalize to a large task family? In this paper, we investigate task generalization through the lens of AutoRegressive Compositional (ARC) structure, where each task is a composition of $T$ operations, and each operation is among a finite family of $\d$ subtasks. This yields a total class of size~\( \d^\TT \). We first show that generalization to all \( \d^\TT \) tasks is theoretically achievable by training on only \( \tilde{O}(\d) \) tasks. Empirically, we demonstrate that Transformers achieve such exponential task generalization on sparse parity functions via in-context learning (ICL) and Chain-of-Thought (CoT) reasoning. We further demonstrate this generalization in arithmetic and language translation, extending beyond parity functions.

Goedel-Prover: A Frontier Model for Open-Source Automated Theorem Proving

We introduce Goedel-Prover, an open-source large language model (LLM) that achieves the state-of-the-art (SOTA) performance in automated formal proof generation for mathematical problems. The key challenge in this field is the scarcity of formalized math statements and proofs, which we tackle in the following ways. We train statement formalizers to translate the natural language math problems from Numina into formal language (Lean 4), creating a dataset of 1.64 million formal statements. LLMs are used to check that the formal statements accurately preserve the content of the original natural language problems. We then iteratively build a large dataset of formal proofs by training a series of provers. Each prover succeeds in proving many statements that the previous ones could not, and these new proofs are added to the training set for the next prover. The final prover outperforms all existing open-source models in whole-proof generation. On the miniF2F benchmark, it achieves a 57.6% success rate (Pass@32), exceeding the previous best open-source model by 7.6%. On PutnamBench, Goedel-Prover successfully solves 7 problems (Pass@512), ranking first on the leaderboard. Furthermore, it generates 29.7K formal proofs for Lean Workbook problems, nearly doubling the 15.7K produced by earlier works.

From Sparse Dependence to Sparse Attention: Unveiling How Chain-of-Thought Enhances Transformer Sample Efficiency

Chain-of-thought (CoT) significantly enhances the reasoning performance of large language models (LLM). While current theoretical studies often attribute this improvement to increased expressiveness and computational capacity, we argue that expressiveness is not the primary limitation in the LLM regime, as current large models will fail on simple tasks. Using a parity-learning setup, we demonstrate that CoT can substantially improve sample efficiency even when the representation power is sufficient. Specifically, with CoT, a transformer can learn the function within polynomial samples, whereas without CoT, the required sample size is exponential. Additionally, we show that CoT simplifies the learning process by introducing sparse sequential dependencies among input tokens, and leads to a sparse and interpretable attention. We validate our theoretical analysis with both synthetic and real-world experiments, confirming that sparsity in attention layers is a key factor of the improvement induced by CoT.

Unmemorization in Large Language Models via Self-Distillation and Deliberate Imagination

While displaying impressive generation capabilities across many tasks, Large Language Models (LLMs) still struggle with crucial issues of privacy violation and unwanted exposure of sensitive data. This raises an essential question: how should we prevent such undesired behavior of LLMs while maintaining their strong generation and natural language understanding (NLU) capabilities? In this work, we introduce a novel approach termed deliberate imagination in the context of LLM unlearning. Instead of trying to forget memorized data, we employ a self-distillation framework, guiding LLMs to deliberately imagine alternative scenarios. As demonstrated in a wide range of experiments, the proposed method not only effectively unlearns targeted text but also preserves the LLMs' capabilities in open-ended generation tasks as well as in NLU tasks. Our results demonstrate the usefulness of this approach across different models and sizes, and also with parameter-efficient fine-tuning, offering a novel pathway to addressing the challenges with private and sensitive data in LLM applications.

Deep hybrid model with satellite imagery: how to combine demand modeling and computer vision for behavior analysis?

Classical demand modeling analyzes travel behavior using only low-dimensional numeric data (i.e. sociodemographics and travel attributes) but not high-dimensional urban imagery. However, travel behavior depends on the factors represented by both numeric data and urban imagery, thus necessitating a synergetic framework to combine them. This study creates a theoretical framework of deep hybrid models with a crossing structure consisting of a mixing operator and a behavioral predictor, thus integrating the numeric and imagery data into a latent space. Empirically, this framework is applied to analyze travel mode choice using the MyDailyTravel Survey from Chicago as the numeric inputs and the satellite images as the imagery inputs. We found that deep hybrid models outperform both the traditional demand models and the recent deep learning in predicting the aggregate and disaggregate travel behavior with our supervision-as-mixing design. The latent space in deep hybrid models can be interpreted, because it reveals meaningful spatial and social patterns. The deep hybrid models can also generate new urban images that do not exist in reality and interpret them with economic theory, such as computing substitution patterns and social welfare changes. Overall, the deep hybrid models demonstrate the complementarity between the low-dimensional numeric and high-dimensional imagery data and between the traditional demand modeling and recent deep learning. It generalizes the latent classes and variables in classical hybrid demand models to a latent space, and leverages the computational power of deep learning for imagery while retaining the economic interpretability on the microeconomics foundation.

IDEAL: Inexact DEcentralized Accelerated Augmented Lagrangian Method

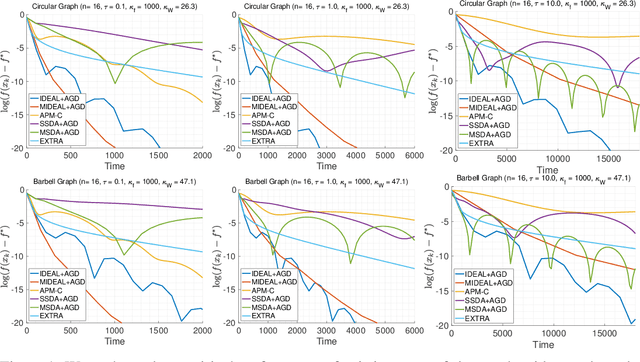
We introduce a framework for designing primal methods under the decentralized optimization setting where local functions are smooth and strongly convex. Our approach consists of approximately solving a sequence of sub-problems induced by the accelerated augmented Lagrangian method, thereby providing a systematic way for deriving several well-known decentralized algorithms including EXTRA arXiv:1404.6264 and SSDA arXiv:1702.08704. When coupled with accelerated gradient descent, our framework yields a novel primal algorithm whose convergence rate is optimal and matched by recently derived lower bounds. We provide experimental results that demonstrate the effectiveness of the proposed algorithm on highly ill-conditioned problems.

Stochastic Optimization with Non-stationary Noise

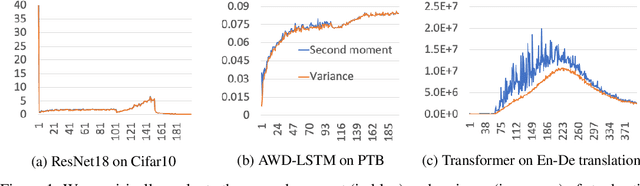
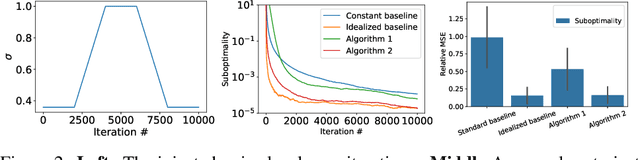
We investigate stochastic optimization problems under relaxed assumptions on the distribution of noise that are motivated by empirical observations in neural network training. Standard results on optimal convergence rates for stochastic optimization assume either there exists a uniform bound on the moments of the gradient noise, or that the noise decays as the algorithm progresses. These assumptions do not match the empirical behavior of optimization algorithms used in neural network training where the noise level in stochastic gradients could even increase with time. We address this behavior by studying convergence rates of stochastic gradient methods subject to changing second moment (or variance) of the stochastic oracle as the iterations progress. When the variation in the noise is known, we show that it is always beneficial to adapt the step-size and exploit the noise variability. When the noise statistics are unknown, we obtain similar improvements by developing an online estimator of the noise level, thereby recovering close variants of RMSProp. Consequently, our results reveal an important scenario where adaptive stepsize methods outperform SGD.

On Complexity of Finding Stationary Points of Nonsmooth Nonconvex Functions

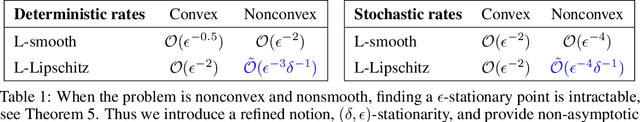
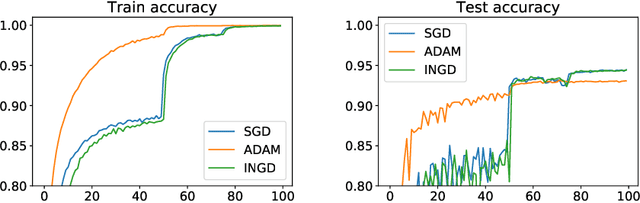
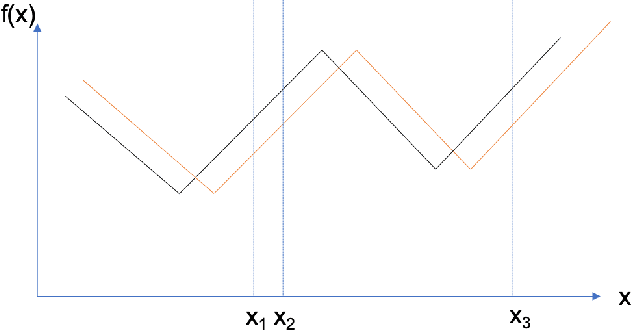
We provide the first \emph{non-asymptotic} analysis for finding stationary points of nonsmooth, nonconvex functions. In particular, we study the class of Hadamard semi-differentiable functions, perhaps the largest class of nonsmooth functions for which the chain rule of calculus holds. This class contains important examples such as ReLU neural networks and others with non-differentiable activation functions. First, we show that finding an $\epsilon$-stationary point with first-order methods is impossible in finite time. Therefore, we introduce the notion of \emph{$(\delta, \epsilon)$-stationarity}, a generalization that allows for a point to be within distance $\delta$ of an $\epsilon$-stationary point and reduces to $\epsilon$-stationarity for smooth functions. We propose a series of randomized first-order methods and analyze their complexity of finding a $(\delta, \epsilon)$-stationary point. Furthermore, we provide a lower bound and show that our stochastic algorithm has min-max optimal dependence on $\delta$. Empirically, our methods perform well for training ReLU neural networks.