On Complexity of Finding Stationary Points of Nonsmooth Nonconvex Functions

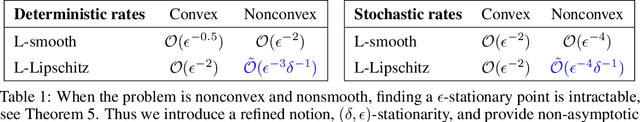
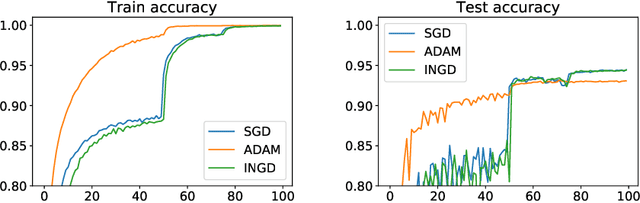
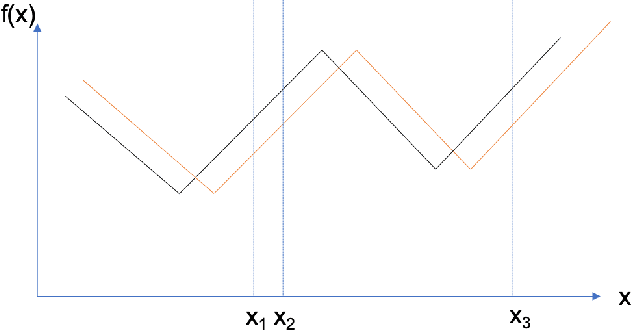
We provide the first \emph{non-asymptotic} analysis for finding stationary points of nonsmooth, nonconvex functions. In particular, we study the class of Hadamard semi-differentiable functions, perhaps the largest class of nonsmooth functions for which the chain rule of calculus holds. This class contains important examples such as ReLU neural networks and others with non-differentiable activation functions. First, we show that finding an $\epsilon$-stationary point with first-order methods is impossible in finite time. Therefore, we introduce the notion of \emph{$(\delta, \epsilon)$-stationarity}, a generalization that allows for a point to be within distance $\delta$ of an $\epsilon$-stationary point and reduces to $\epsilon$-stationarity for smooth functions. We propose a series of randomized first-order methods and analyze their complexity of finding a $(\delta, \epsilon)$-stationary point. Furthermore, we provide a lower bound and show that our stochastic algorithm has min-max optimal dependence on $\delta$. Empirically, our methods perform well for training ReLU neural networks.