A projection-based framework for gradient-free and parallel learning

We present a feasibility-seeking approach to neural network training. This mathematical optimization framework is distinct from conventional gradient-based loss minimization and uses projection operators and iterative projection algorithms. We reformulate training as a large-scale feasibility problem: finding network parameters and states that satisfy local constraints derived from its elementary operations. Training then involves projecting onto these constraints, a local operation that can be parallelized across the network. We introduce PJAX, a JAX-based software framework that enables this paradigm. PJAX composes projection operators for elementary operations, automatically deriving the solution operators for the feasibility problems (akin to autodiff for derivatives). It inherently supports GPU/TPU acceleration, provides a familiar NumPy-like API, and is extensible. We train diverse architectures (MLPs, CNNs, RNNs) on standard benchmarks using PJAX, demonstrating its functionality and generality. Our results show that this approach is as a compelling alternative to gradient-based training, with clear advantages in parallelism and the ability to handle non-differentiable operations.

Revisiting Frank-Wolfe for Structured Nonconvex Optimization

We introduce a new projection-free (Frank-Wolfe) method for optimizing structured nonconvex functions that are expressed as a difference of two convex functions. This problem class subsumes smooth nonconvex minimization, positioning our method as a promising alternative to the classical Frank-Wolfe algorithm. DC decompositions are not unique; by carefully selecting a decomposition, we can better exploit the problem structure, improve computational efficiency, and adapt to the underlying problem geometry to find better local solutions. We prove that the proposed method achieves a first-order stationary point in $O(1/\epsilon^2)$ iterations, matching the complexity of the standard Frank-Wolfe algorithm for smooth nonconvex minimization in general. Specific decompositions can, for instance, yield a gradient-efficient variant that requires only $O(1/\epsilon)$ calls to the gradient oracle. Finally, we present numerical experiments demonstrating the effectiveness of the proposed method compared to the standard Frank-Wolfe algorithm.

Implicit Bias in Matrix Factorization and its Explicit Realization in a New Architecture

Gradient descent for matrix factorization is known to exhibit an implicit bias toward approximately low-rank solutions. While existing theories often assume the boundedness of iterates, empirically the bias persists even with unbounded sequences. We thus hypothesize that implicit bias is driven by divergent dynamics markedly different from the convergent dynamics for data fitting. Using this perspective, we introduce a new factorization model: $X\approx UDV^\top$, where $U$ and $V$ are constrained within norm balls, while $D$ is a diagonal factor allowing the model to span the entire search space. Our experiments reveal that this model exhibits a strong implicit bias regardless of initialization and step size, yielding truly (rather than approximately) low-rank solutions. Furthermore, drawing parallels between matrix factorization and neural networks, we propose a novel neural network model featuring constrained layers and diagonal components. This model achieves strong performance across various regression and classification tasks while finding low-rank solutions, resulting in efficient and lightweight networks.

Graph Transformers Dream of Electric Flow

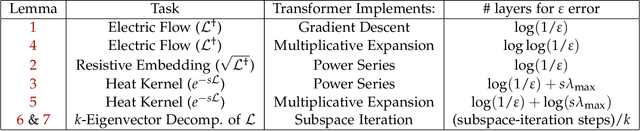
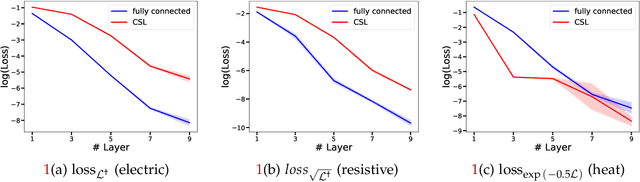
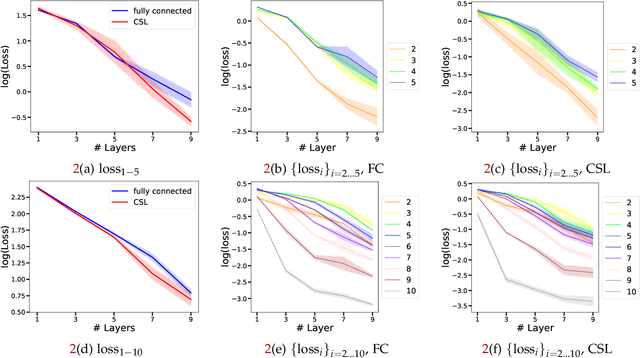
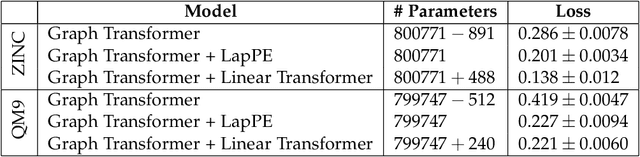
We show theoretically and empirically that the linear Transformer, when applied to graph data, can implement algorithms that solve canonical problems such as electric flow and eigenvector decomposition. The input to the Transformer is simply the graph incidence matrix; no other explicit positional encoding information is provided. We present explicit weight configurations for implementing each such graph algorithm, and we bound the errors of the constructed Transformers by the errors of the underlying algorithms. Our theoretical findings are corroborated by experiments on synthetic data. Additionally, on a real-world molecular regression task, we observe that the linear Transformer is capable of learning a more effective positional encoding than the default one based on Laplacian eigenvectors. Our work is an initial step towards elucidating the inner-workings of the Transformer for graph data.

Memory-augmented Transformers can implement Linear First-Order Optimization Methods

We show that memory-augmented Transformers (Memformers) can implement linear first-order optimization methods such as conjugate gradient descent, momentum methods, and more generally, methods that linearly combine past gradients. Building on prior work that demonstrates how Transformers can simulate preconditioned gradient descent, we provide theoretical and empirical evidence that Memformers can learn more advanced optimization algorithms. Specifically, we analyze how memory registers in Memformers store suitable intermediate attention values allowing them to implement algorithms such as conjugate gradient. Our results show that Memformers can efficiently learn these methods by training on random linear regression tasks, even learning methods that outperform conjugate gradient. This work extends our knowledge about the algorithmic capabilities of Transformers, showing how they can learn complex optimization methods.

First-Order Methods for Linearly Constrained Bilevel Optimization

Algorithms for bilevel optimization often encounter Hessian computations, which are prohibitive in high dimensions. While recent works offer first-order methods for unconstrained bilevel problems, the constrained setting remains relatively underexplored. We present first-order linearly constrained optimization methods with finite-time hypergradient stationarity guarantees. For linear equality constraints, we attain $\epsilon$-stationarity in $\widetilde{O}(\epsilon^{-2})$ gradient oracle calls, which is nearly-optimal. For linear inequality constraints, we attain $(\delta,\epsilon)$-Goldstein stationarity in $\widetilde{O}(d{\delta^{-1} \epsilon^{-3}})$ gradient oracle calls, where $d$ is the upper-level dimension. Finally, we obtain for the linear inequality setting dimension-free rates of $\widetilde{O}({\delta^{-1} \epsilon^{-4}})$ oracle complexity under the additional assumption of oracle access to the optimal dual variable. Along the way, we develop new nonsmooth nonconvex optimization methods with inexact oracles. We verify these guarantees with preliminary numerical experiments.

Riemannian Bilevel Optimization

We develop new algorithms for Riemannian bilevel optimization. We focus in particular on batch and stochastic gradient-based methods, with the explicit goal of avoiding second-order information such as Riemannian hyper-gradients. We propose and analyze $\mathrm{RF^2SA}$, a method that leverages first-order gradient information to navigate the complex geometry of Riemannian manifolds efficiently. Notably, $\mathrm{RF^2SA}$ is a single-loop algorithm, and thus easier to implement and use. Under various setups, including stochastic optimization, we provide explicit convergence rates for reaching $\epsilon$-stationary points. We also address the challenge of optimizing over Riemannian manifolds with constraints by adjusting the multiplier in the Lagrangian, ensuring convergence to the desired solution without requiring access to second-order derivatives.

Efficient Sampling on Riemannian Manifolds via Langevin MCMC

We study the task of efficiently sampling from a Gibbs distribution $d \pi^* = e^{-h} d {vol}_g$ over a Riemannian manifold $M$ via (geometric) Langevin MCMC; this algorithm involves computing exponential maps in random Gaussian directions and is efficiently implementable in practice. The key to our analysis of Langevin MCMC is a bound on the discretization error of the geometric Euler-Murayama scheme, assuming $\nabla h$ is Lipschitz and $M$ has bounded sectional curvature. Our error bound matches the error of Euclidean Euler-Murayama in terms of its stepsize dependence. Combined with a contraction guarantee for the geometric Langevin Diffusion under Kendall-Cranston coupling, we prove that the Langevin MCMC iterates lie within $\epsilon$-Wasserstein distance of $\pi^*$ after $\tilde{O}(\epsilon^{-2})$ steps, which matches the iteration complexity for Euclidean Langevin MCMC. Our results apply in general settings where $h$ can be nonconvex and $M$ can have negative Ricci curvature. Under additional assumptions that the Riemannian curvature tensor has bounded derivatives, and that $\pi^*$ satisfies a $CD(\cdot,\infty)$ condition, we analyze the stochastic gradient version of Langevin MCMC, and bound its iteration complexity by $\tilde{O}(\epsilon^{-2})$ as well.

Transformers Implement Functional Gradient Descent to Learn Non-Linear Functions In Context

Many neural network architectures have been shown to be Turing Complete, and can thus implement arbitrary algorithms. However, Transformers are unique in that they can implement gradient-based learning algorithms \emph{under simple parameter configurations}. A line of recent work shows that linear Transformers naturally learn to implement gradient descent (GD) when trained on a linear regression in-context learning task. But the linearity assumption (either in the Transformer architecture or in the learning task) is far from realistic settings where non-linear activations crucially enable Transformers to learn complicated non-linear functions. In this paper, we provide theoretical and empirical evidence that non-linear Transformers can, and \emph{in fact do}, learn to implement learning algorithms to learn non-linear functions in context. Our results apply to a broad class of combinations of non-linear architectures, and non-linear in-context learning tasks. Interestingly, we show that the optimal choice of non-linear activation depends in a natural way on the non-linearity of the learning task.

Linear attention is (maybe) all you need (to understand transformer optimization)

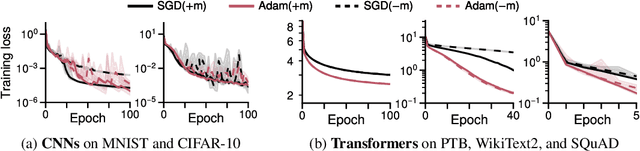
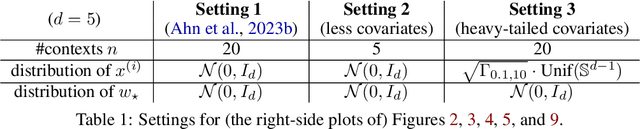
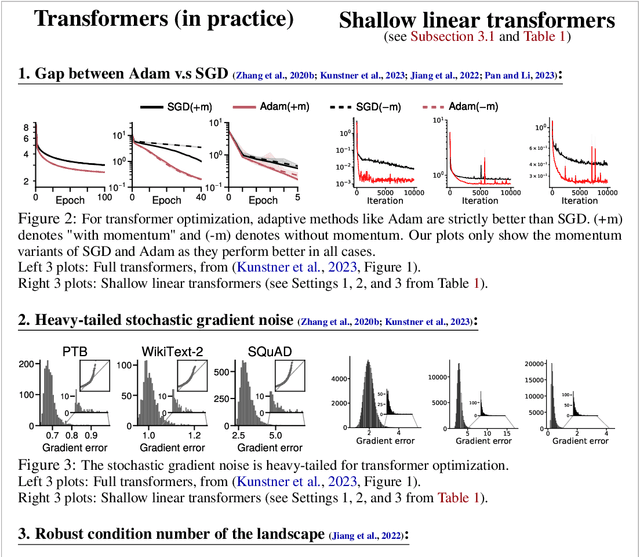
Transformer training is notoriously difficult, requiring a careful design of optimizers and use of various heuristics. We make progress towards understanding the subtleties of training transformers by carefully studying a simple yet canonical linearized shallow transformer model. Specifically, we train linear transformers to solve regression tasks, inspired by J. von Oswald et al. (ICML 2023), and K. Ahn et al. (NeurIPS 2023). Most importantly, we observe that our proposed linearized models can reproduce several prominent aspects of transformer training dynamics. Consequently, the results obtained in this paper suggest that a simple linearized transformer model could actually be a valuable, realistic abstraction for understanding transformer optimization.