Understanding Sharpness Dynamics in NN Training with a Minimalist Example: The Effects of Dataset Difficulty, Depth, Stochasticity, and More

When training deep neural networks with gradient descent, sharpness often increases -- a phenomenon known as progressive sharpening -- before saturating at the edge of stability. Although commonly observed in practice, the underlying mechanisms behind progressive sharpening remain poorly understood. In this work, we study this phenomenon using a minimalist model: a deep linear network with a single neuron per layer. We show that this simple model effectively captures the sharpness dynamics observed in recent empirical studies, offering a simple testbed to better understand neural network training. Moreover, we theoretically analyze how dataset properties, network depth, stochasticity of optimizers, and step size affect the degree of progressive sharpening in the minimalist model. We then empirically demonstrate how these theoretical insights extend to practical scenarios. This study offers a deeper understanding of sharpness dynamics in neural network training, highlighting the interplay between depth, training data, and optimizers.

Understanding the Performance Gap in Preference Learning: A Dichotomy of RLHF and DPO

We present a fine-grained theoretical analysis of the performance gap between reinforcement learning from human feedback (RLHF) and direct preference optimization (DPO) under a representation gap. Our study decomposes this gap into two sources: an explicit representation gap under exact optimization and an implicit representation gap under finite samples. In the exact optimization setting, we characterize how the relative capacities of the reward and policy model classes influence the final policy qualities. We show that RLHF, DPO, or online DPO can outperform one another depending on the type of model mis-specifications. Notably, online DPO can outperform both RLHF and standard DPO when the reward and policy model classes are isomorphic and both mis-specified. In the approximate optimization setting, we provide a concrete construction where the ground-truth reward is implicitly sparse and show that RLHF requires significantly fewer samples than DPO to recover an effective reward model -- highlighting a statistical advantage of two-stage learning. Together, these results provide a comprehensive understanding of the performance gap between RLHF and DPO under various settings, and offer practical insights into when each method is preferred.

Does SGD really happen in tiny subspaces?

Understanding the training dynamics of deep neural networks is challenging due to their high-dimensional nature and intricate loss landscapes. Recent studies have revealed that, along the training trajectory, the gradient approximately aligns with a low-rank top eigenspace of the training loss Hessian, referred to as the dominant subspace. Given this alignment, this paper explores whether neural networks can be trained within the dominant subspace, which, if feasible, could lead to more efficient training methods. Our primary observation is that when the SGD update is projected onto the dominant subspace, the training loss does not decrease further. This suggests that the observed alignment between the gradient and the dominant subspace is spurious. Surprisingly, projecting out the dominant subspace proves to be just as effective as the original update, despite removing the majority of the original update component. Similar observations are made for the large learning rate regime (also known as Edge of Stability) and Sharpness-Aware Minimization. We discuss the main causes and implications of this spurious alignment, shedding light on the intricate dynamics of neural network training.

Linear attention is (maybe) all you need (to understand transformer optimization)

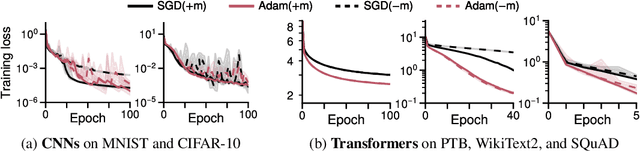
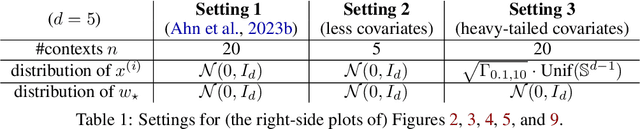
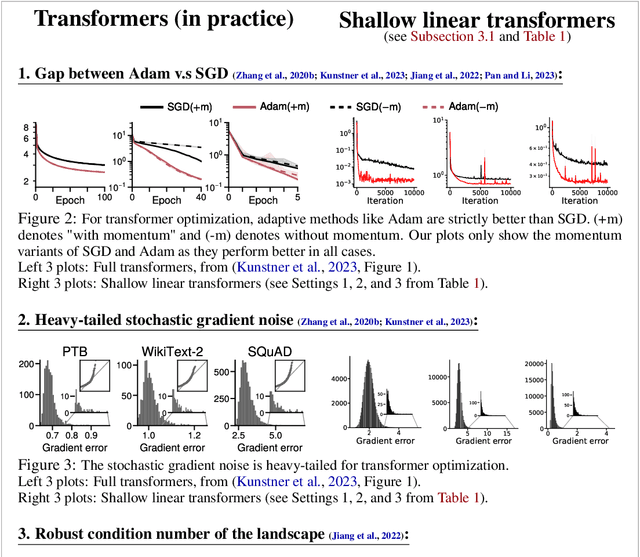
Transformer training is notoriously difficult, requiring a careful design of optimizers and use of various heuristics. We make progress towards understanding the subtleties of training transformers by carefully studying a simple yet canonical linearized shallow transformer model. Specifically, we train linear transformers to solve regression tasks, inspired by J. von Oswald et al. (ICML 2023), and K. Ahn et al. (NeurIPS 2023). Most importantly, we observe that our proposed linearized models can reproduce several prominent aspects of transformer training dynamics. Consequently, the results obtained in this paper suggest that a simple linearized transformer model could actually be a valuable, realistic abstraction for understanding transformer optimization.

Trajectory Alignment: Understanding the Edge of Stability Phenomenon via Bifurcation Theory

Cohen et al. (2021) empirically study the evolution of the largest eigenvalue of the loss Hessian, also known as sharpness, along the gradient descent (GD) trajectory and observe a phenomenon called the Edge of Stability (EoS). The sharpness increases at the early phase of training (referred to as progressive sharpening), and eventually saturates close to the threshold of $2 / \text{(step size)}$. In this paper, we start by demonstrating through empirical studies that when the EoS phenomenon occurs, different GD trajectories (after a proper reparameterization) align on a specific bifurcation diagram independent of initialization. We then rigorously prove this trajectory alignment phenomenon for a two-layer fully-connected linear network and a single-neuron nonlinear network trained with a single data point. Our trajectory alignment analysis establishes both progressive sharpening and EoS phenomena, encompassing and extending recent findings in the literature.