General framework for online-to-nonconvex conversion: Schedule-free SGD is also effective for nonconvex optimization

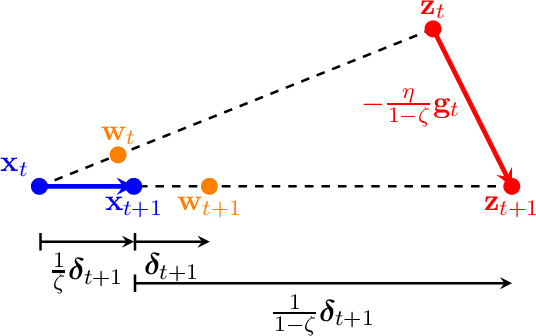
This work investigates the effectiveness of schedule-free methods, developed by A. Defazio et al. (NeurIPS 2024), in nonconvex optimization settings, inspired by their remarkable empirical success in training neural networks. Specifically, we show that schedule-free SGD achieves optimal iteration complexity for nonsmooth, nonconvex optimization problems. Our proof begins with the development of a general framework for online-to-nonconvex conversion, which converts a given online learning algorithm into an optimization algorithm for nonconvex losses. Our general framework not only recovers existing conversions but also leads to two novel conversion schemes. Notably, one of these new conversions corresponds directly to schedule-free SGD, allowing us to establish its optimality. Additionally, our analysis provides valuable insights into the parameter choices for schedule-free SGD, addressing a theoretical gap that the convex theory cannot explain.

Learning to Achieve Goals with Belief State Transformers

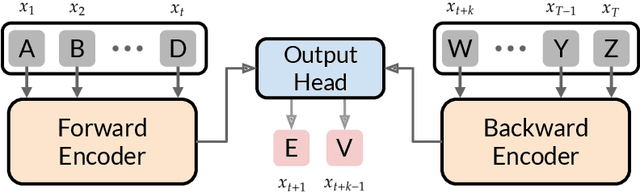
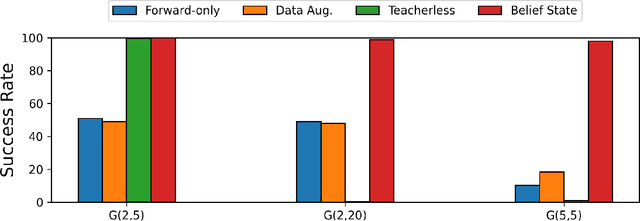
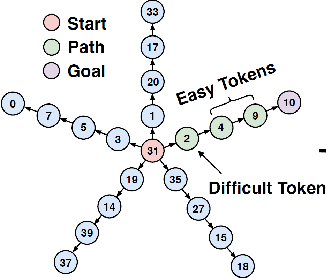
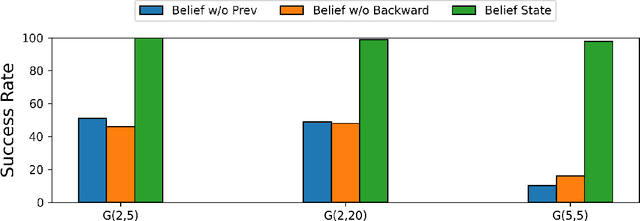
We introduce the "Belief State Transformer", a next-token predictor that takes both a prefix and suffix as inputs, with a novel objective of predicting both the next token for the prefix and the previous token for the suffix. The Belief State Transformer effectively learns to solve challenging problems that conventional forward-only transformers struggle with, in a domain-independent fashion. Key to this success is learning a compact belief state that captures all relevant information necessary for accurate predictions. Empirical ablations show that each component of the model is essential in difficult scenarios where standard Transformers fall short. For the task of story writing with known prefixes and suffixes, our approach outperforms the Fill-in-the-Middle method for reaching known goals and demonstrates improved performance even when the goals are unknown. Altogether, the Belief State Transformer enables more efficient goal-conditioned decoding, better test-time inference, and high-quality text representations on small scale problems.

Improved Sample Complexity of Imitation Learning for Barrier Model Predictive Control

Recent work in imitation learning has shown that having an expert controller that is both suitably smooth and stable enables stronger guarantees on the performance of the learned controller. However, constructing such smoothed expert controllers for arbitrary systems remains challenging, especially in the presence of input and state constraints. As our primary contribution, we show how such a smoothed expert can be designed for a general class of systems using a log-barrier-based relaxation of a standard Model Predictive Control (MPC) optimization problem. Improving upon our previous work, we show that barrier MPC achieves theoretically optimal error-to-smoothness tradeoff along some direction. At the core of this theoretical guarantee on smoothness is an improved lower bound we prove on the optimality gap of the analytic center associated with a convex Lipschitz function, which we believe could be of independent interest. We validate our theoretical findings via experiments, demonstrating the merits of our smoothing approach over randomized smoothing.

Adam with model exponential moving average is effective for nonconvex optimization

In this work, we offer a theoretical analysis of two modern optimization techniques for training large and complex models: (i) adaptive optimization algorithms, such as Adam, and (ii) the model exponential moving average (EMA). Specifically, we demonstrate that a clipped version of Adam with model EMA achieves the optimal convergence rates in various nonconvex optimization settings, both smooth and nonsmooth. Moreover, when the scale varies significantly across different coordinates, we demonstrate that the coordinate-wise adaptivity of Adam is provably advantageous. Notably, unlike previous analyses of Adam, our analysis crucially relies on its core elements -- momentum and discounting factors -- as well as model EMA, motivating their wide applications in practice.

Does SGD really happen in tiny subspaces?

Understanding the training dynamics of deep neural networks is challenging due to their high-dimensional nature and intricate loss landscapes. Recent studies have revealed that, along the training trajectory, the gradient approximately aligns with a low-rank top eigenspace of the training loss Hessian, referred to as the dominant subspace. Given this alignment, this paper explores whether neural networks can be trained within the dominant subspace, which, if feasible, could lead to more efficient training methods. Our primary observation is that when the SGD update is projected onto the dominant subspace, the training loss does not decrease further. This suggests that the observed alignment between the gradient and the dominant subspace is spurious. Surprisingly, projecting out the dominant subspace proves to be just as effective as the original update, despite removing the majority of the original update component. Similar observations are made for the large learning rate regime (also known as Edge of Stability) and Sharpness-Aware Minimization. We discuss the main causes and implications of this spurious alignment, shedding light on the intricate dynamics of neural network training.

Understanding Adam Optimizer via Online Learning of Updates: Adam is FTRL in Disguise

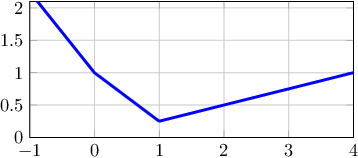
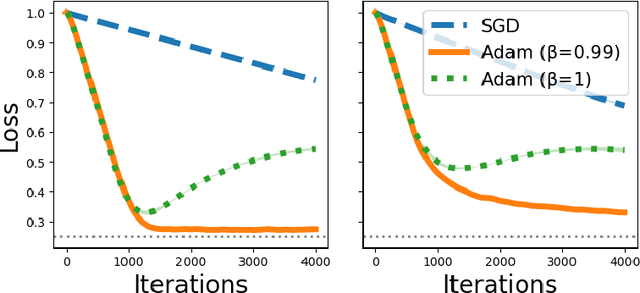
Despite the success of the Adam optimizer in practice, the theoretical understanding of its algorithmic components still remains limited. In particular, most existing analyses of Adam show the convergence rate that can be simply achieved by non-adative algorithms like SGD. In this work, we provide a different perspective based on online learning that underscores the importance of Adam's algorithmic components. Inspired by Cutkosky et al. (2023), we consider the framework called online learning of updates, where we choose the updates of an optimizer based on an online learner. With this framework, the design of a good optimizer is reduced to the design of a good online learner. Our main observation is that Adam corresponds to a principled online learning framework called Follow-the-Regularized-Leader (FTRL). Building on this observation, we study the benefits of its algorithmic components from the online learning perspective.

Linear attention is (maybe) all you need (to understand transformer optimization)

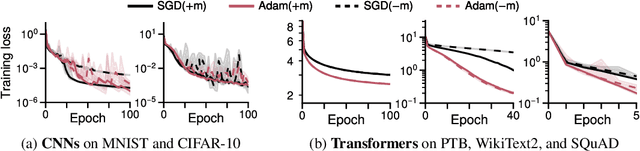
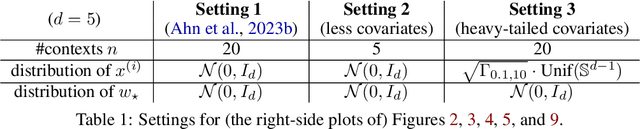
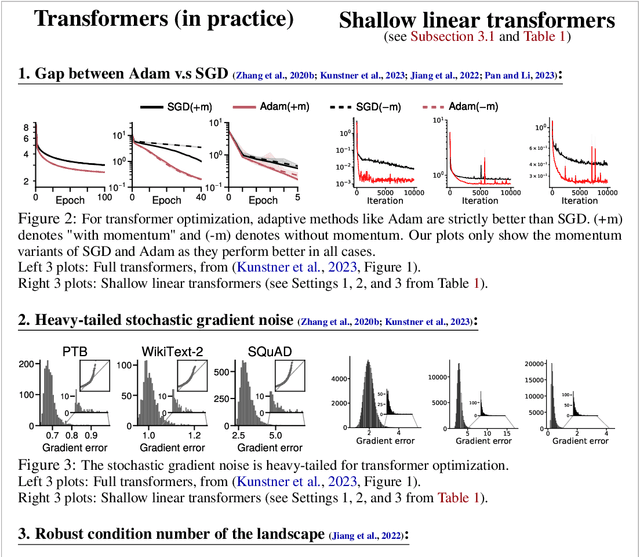
Transformer training is notoriously difficult, requiring a careful design of optimizers and use of various heuristics. We make progress towards understanding the subtleties of training transformers by carefully studying a simple yet canonical linearized shallow transformer model. Specifically, we train linear transformers to solve regression tasks, inspired by J. von Oswald et al. (ICML 2023), and K. Ahn et al. (NeurIPS 2023). Most importantly, we observe that our proposed linearized models can reproduce several prominent aspects of transformer training dynamics. Consequently, the results obtained in this paper suggest that a simple linearized transformer model could actually be a valuable, realistic abstraction for understanding transformer optimization.

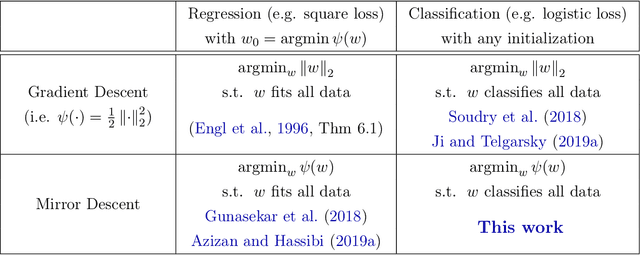
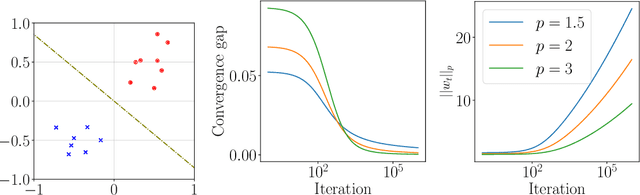
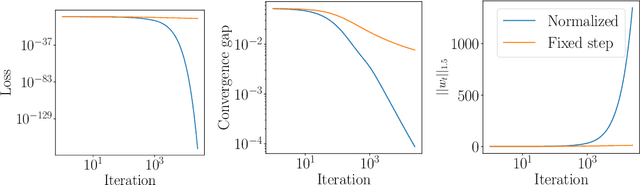
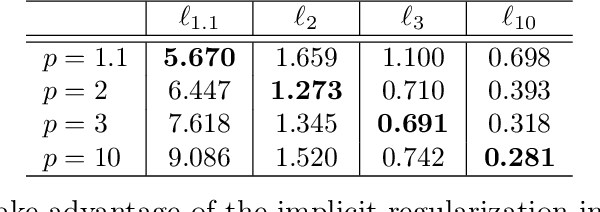
A Unified Approach to Controlling Implicit Regularization via Mirror Descent

Inspired by the remarkable success of deep neural networks, there has been significant interest in understanding the generalization performance of overparameterized models. Substantial efforts have been invested in characterizing how optimization algorithms impact generalization through their "preferred" solutions, a phenomenon commonly referred to as implicit regularization. In particular, it has been argued that gradient descent (GD) induces an implicit $\ell_2$-norm regularization in regression and classification problems. However, the implicit regularization of different algorithms are confined to either a specific geometry or a particular class of learning problems, indicating a gap in a general approach for controlling the implicit regularization. To address this, we present a unified approach using mirror descent (MD), a notable generalization of GD, to control implicit regularization in both regression and classification settings. More specifically, we show that MD with the general class of homogeneous potential functions converges in direction to a generalized maximum-margin solution for linear classification problems, thereby answering a long-standing question in the classification setting. Further, we show that MD can be implemented efficiently and under suitable conditions, enjoys fast convergence. Through comprehensive experiments, we demonstrate that MD is a versatile method to produce learned models with different regularizers, which in turn have different generalization performances.

Smooth Model Predictive Control with Applications to Statistical Learning

Statistical learning theory and high dimensional statistics have had a tremendous impact on Machine Learning theory and have impacted a variety of domains including systems and control theory. Over the past few years we have witnessed a variety of applications of such theoretical tools to help answer questions such as: how many state-action pairs are needed to learn a static control policy to a given accuracy? Recent results have shown that continuously differentiable and stabilizing control policies can be well-approximated using neural networks with hard guarantees on performance, yet often even the simplest constrained control problems are not smooth. To address this void, in this paper we study smooth approximations of linear Model Predictive Control (MPC) policies, in which hard constraints are replaced by barrier functions, a.k.a. barrier MPC. In particular, we show that barrier MPC inherits the exponential stability properties of the original non-smooth MPC policy. Using a careful analysis of the proposed barrier MPC, we show that its smoothness constant can be carefully controlled, thereby paving the way for new sample complexity results for approximating MPC policies from sampled state-action pairs.

Transformers learn to implement preconditioned gradient descent for in-context learning

Motivated by the striking ability of transformers for in-context learning, several works demonstrate that transformers can implement algorithms like gradient descent. By a careful construction of weights, these works show that multiple layers of transformers are expressive enough to simulate gradient descent iterations. Going beyond the question of expressivity, we ask: Can transformers learn to implement such algorithms by training over random problem instances? To our knowledge, we make the first theoretical progress toward this question via analysis of the loss landscape for linear transformers trained over random instances of linear regression. For a single attention layer, we prove the global minimum of the training objective implements a single iteration of preconditioned gradient descent. Notably, the preconditioning matrix not only adapts to the input distribution but also to the variance induced by data inadequacy. For a transformer with $k$ attention layers, we prove certain critical points of the training objective implement $k$ iterations of preconditioned gradient descent. Our results call for future theoretical studies on learning algorithms by training transformers.