Understanding Sharpness Dynamics in NN Training with a Minimalist Example: The Effects of Dataset Difficulty, Depth, Stochasticity, and More

When training deep neural networks with gradient descent, sharpness often increases -- a phenomenon known as progressive sharpening -- before saturating at the edge of stability. Although commonly observed in practice, the underlying mechanisms behind progressive sharpening remain poorly understood. In this work, we study this phenomenon using a minimalist model: a deep linear network with a single neuron per layer. We show that this simple model effectively captures the sharpness dynamics observed in recent empirical studies, offering a simple testbed to better understand neural network training. Moreover, we theoretically analyze how dataset properties, network depth, stochasticity of optimizers, and step size affect the degree of progressive sharpening in the minimalist model. We then empirically demonstrate how these theoretical insights extend to practical scenarios. This study offers a deeper understanding of sharpness dynamics in neural network training, highlighting the interplay between depth, training data, and optimizers.

Incremental Gradient Descent with Small Epoch Counts is Surprisingly Slow on Ill-Conditioned Problems

Recent theoretical results demonstrate that the convergence rates of permutation-based SGD (e.g., random reshuffling SGD) are faster than uniform-sampling SGD; however, these studies focus mainly on the large epoch regime, where the number of epochs $K$ exceeds the condition number $\kappa$. In contrast, little is known when $K$ is smaller than $\kappa$, and it is still a challenging open question whether permutation-based SGD can converge faster in this small epoch regime (Safran and Shamir, 2021). As a step toward understanding this gap, we study the naive deterministic variant, Incremental Gradient Descent (IGD), on smooth and strongly convex functions. Our lower bounds reveal that for the small epoch regime, IGD can exhibit surprisingly slow convergence even when all component functions are strongly convex. Furthermore, when some component functions are allowed to be nonconvex, we prove that the optimality gap of IGD can be significantly worse throughout the small epoch regime. Our analyses reveal that the convergence properties of permutation-based SGD in the small epoch regime may vary drastically depending on the assumptions on component functions. Lastly, we supplement the paper with tight upper and lower bounds for IGD in the large epoch regime.

Convergence and Implicit Bias of Gradient Descent on Continual Linear Classification

We study continual learning on multiple linear classification tasks by sequentially running gradient descent (GD) for a fixed budget of iterations per task. When all tasks are jointly linearly separable and are presented in a cyclic/random order, we show the directional convergence of the trained linear classifier to the joint (offline) max-margin solution. This is surprising because GD training on a single task is implicitly biased towards the individual max-margin solution for the task, and the direction of the joint max-margin solution can be largely different from these individual solutions. Additionally, when tasks are given in a cyclic order, we present a non-asymptotic analysis on cycle-averaged forgetting, revealing that (1) alignment between tasks is indeed closely tied to catastrophic forgetting and backward knowledge transfer and (2) the amount of forgetting vanishes to zero as the cycle repeats. Lastly, we analyze the case where the tasks are no longer jointly separable and show that the model trained in a cyclic order converges to the unique minimum of the joint loss function.

Lightweight Dataset Pruning without Full Training via Example Difficulty and Prediction Uncertainty

Recent advances in deep learning rely heavily on massive datasets, leading to substantial storage and training costs. Dataset pruning aims to alleviate this demand by discarding redundant examples. However, many existing methods require training a model with a full dataset over a large number of epochs before being able to prune the dataset, which ironically makes the pruning process more expensive than just training the model on the entire dataset. To overcome this limitation, we introduce a Difficulty and Uncertainty-Aware Lightweight (DUAL) score, which aims to identify important samples from the early training stage by considering both example difficulty and prediction uncertainty. To address a catastrophic accuracy drop at an extreme pruning, we further propose a ratio-adaptive sampling using Beta distribution. Experiments on various datasets and learning scenarios such as image classification with label noise and image corruption, and model architecture generalization demonstrate the superiority of our method over previous state-of-the-art (SOTA) approaches. Specifically, on ImageNet-1k, our method reduces the time cost for pruning to 66% compared to previous methods while achieving a SOTA, specifically 60% test accuracy at a 90% pruning ratio. On CIFAR datasets, the time cost is reduced to just 15% while maintaining SOTA performance.

Stochastic Extragradient with Flip-Flop Shuffling & Anchoring: Provable Improvements

In minimax optimization, the extragradient (EG) method has been extensively studied because it outperforms the gradient descent-ascent method in convex-concave (C-C) problems. Yet, stochastic EG (SEG) has seen limited success in C-C problems, especially for unconstrained cases. Motivated by the recent progress of shuffling-based stochastic methods, we investigate the convergence of shuffling-based SEG in unconstrained finite-sum minimax problems, in search of convergent shuffling-based SEG. Our analysis reveals that both random reshuffling and the recently proposed flip-flop shuffling alone can suffer divergence in C-C problems. However, with an additional simple trick called anchoring, we develop the SEG with flip-flop anchoring (SEG-FFA) method which successfully converges in C-C problems. We also show upper and lower bounds in the strongly-convex-strongly-concave setting, demonstrating that SEG-FFA has a provably faster convergence rate compared to other shuffling-based methods.

Provable Benefit of Cutout and CutMix for Feature Learning

Patch-level data augmentation techniques such as Cutout and CutMix have demonstrated significant efficacy in enhancing the performance of vision tasks. However, a comprehensive theoretical understanding of these methods remains elusive. In this paper, we study two-layer neural networks trained using three distinct methods: vanilla training without augmentation, Cutout training, and CutMix training. Our analysis focuses on a feature-noise data model, which consists of several label-dependent features of varying rarity and label-independent noises of differing strengths. Our theorems demonstrate that Cutout training can learn low-frequency features that vanilla training cannot, while CutMix training can learn even rarer features that Cutout cannot capture. From this, we establish that CutMix yields the highest test accuracy among the three. Our novel analysis reveals that CutMix training makes the network learn all features and noise vectors "evenly" regardless of the rarity and strength, which provides an interesting insight into understanding patch-level augmentation.

DASH: Warm-Starting Neural Network Training in Stationary Settings without Loss of Plasticity

Warm-starting neural network training by initializing networks with previously learned weights is appealing, as practical neural networks are often deployed under a continuous influx of new data. However, it often leads to loss of plasticity, where the network loses its ability to learn new information, resulting in worse generalization than training from scratch. This occurs even under stationary data distributions, and its underlying mechanism is poorly understood. We develop a framework emulating real-world neural network training and identify noise memorization as the primary cause of plasticity loss when warm-starting on stationary data. Motivated by this, we propose Direction-Aware SHrinking (DASH), a method aiming to mitigate plasticity loss by selectively forgetting memorized noise while preserving learned features. e validate our approach on vision tasks, demonstrating improvements in test accuracy and training efficiency.

Arithmetic Transformers Can Length-Generalize in Both Operand Length and Count

Transformers often struggle with length generalization, meaning they fail to generalize to sequences longer than those encountered during training. While arithmetic tasks are commonly used to study length generalization, certain tasks are considered notoriously difficult, e.g., multi-operand addition (requiring generalization over both the number of operands and their lengths) and multiplication (requiring generalization over both operand lengths). In this work, we achieve approximately 2-3x length generalization on both tasks, which is the first such achievement in arithmetic Transformers. We design task-specific scratchpads enabling the model to focus on a fixed number of tokens per each next-token prediction step, and apply multi-level versions of Position Coupling (Cho et al., 2024; McLeish et al., 2024) to let Transformers know the right position to attend to. On the theory side, we prove that a 1-layer Transformer using our method can solve multi-operand addition, up to operand length and operand count that are exponential in embedding dimension.

Position Coupling: Leveraging Task Structure for Improved Length Generalization of Transformers

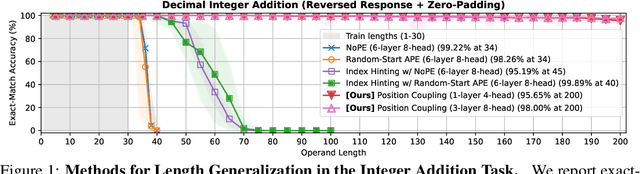
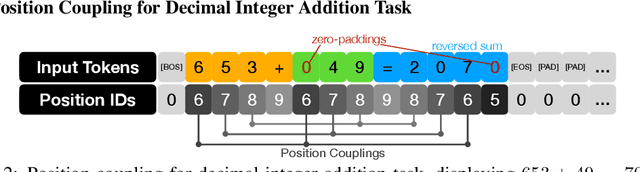
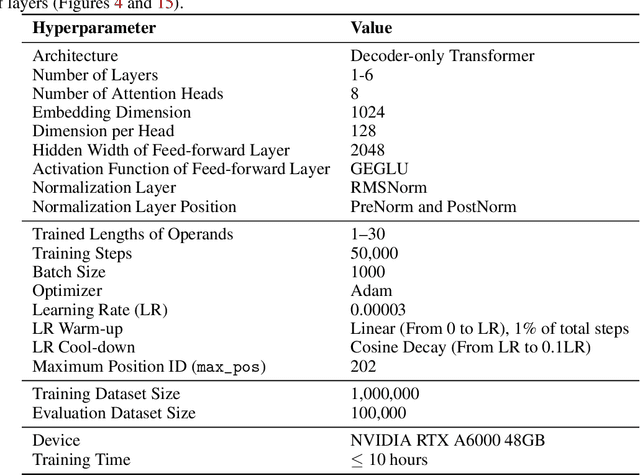
Even for simple arithmetic tasks like integer addition, it is challenging for Transformers to generalize to longer sequences than those encountered during training. To tackle this problem, we propose position coupling, a simple yet effective method that directly embeds the structure of the tasks into the positional encoding of a (decoder-only) Transformer. Taking a departure from the vanilla absolute position mechanism assigning unique position IDs to each of the tokens, we assign the same position IDs to two or more "relevant" tokens; for integer addition tasks, we regard digits of the same significance as in the same position. On the empirical side, we show that with the proposed position coupling, a small (1-layer) Transformer trained on 1 to 30-digit additions can generalize up to 200-digit additions (6.67x of the trained length). On the theoretical side, we prove that a 1-layer Transformer with coupled positions can solve the addition task involving exponentially many digits, whereas any 1-layer Transformer without positional information cannot entirely solve it. We also demonstrate that position coupling can be applied to other algorithmic tasks such as addition with multiple summands, Nx2 multiplication, copy/reverse, and a two-dimensional task.

Does SGD really happen in tiny subspaces?

Understanding the training dynamics of deep neural networks is challenging due to their high-dimensional nature and intricate loss landscapes. Recent studies have revealed that, along the training trajectory, the gradient approximately aligns with a low-rank top eigenspace of the training loss Hessian, referred to as the dominant subspace. Given this alignment, this paper explores whether neural networks can be trained within the dominant subspace, which, if feasible, could lead to more efficient training methods. Our primary observation is that when the SGD update is projected onto the dominant subspace, the training loss does not decrease further. This suggests that the observed alignment between the gradient and the dominant subspace is spurious. Surprisingly, projecting out the dominant subspace proves to be just as effective as the original update, despite removing the majority of the original update component. Similar observations are made for the large learning rate regime (also known as Edge of Stability) and Sharpness-Aware Minimization. We discuss the main causes and implications of this spurious alignment, shedding light on the intricate dynamics of neural network training.