The Coverage Principle: A Framework for Understanding Compositional Generalization

Large language models excel at pattern matching, yet often fall short in systematic compositional generalization. We propose the coverage principle: a data-centric framework showing that models relying primarily on pattern matching for compositional tasks cannot reliably generalize beyond substituting fragments that yield identical results when used in the same contexts. We demonstrate that this framework has a strong predictive power for the generalization capabilities of Transformers. First, we derive and empirically confirm that the training data required for two-hop generalization grows at least quadratically with the token set size, and the training data efficiency does not improve with 20x parameter scaling. Second, for compositional tasks with path ambiguity where one variable affects the output through multiple computational paths, we show that Transformers learn context-dependent state representations that undermine both performance and interoperability. Third, Chain-of-Thought supervision improves training data efficiency for multi-hop tasks but still struggles with path ambiguity. Finally, we outline a \emph{mechanism-based} taxonomy that distinguishes three ways neural networks can generalize: structure-based (bounded by coverage), property-based (leveraging algebraic invariances), and shared-operator (through function reuse). This conceptual lens contextualizes our results and highlights where new architectural ideas are needed to achieve systematic compositionally. Overall, the coverage principle provides a unified lens for understanding compositional reasoning, and underscores the need for fundamental architectural or training innovations to achieve truly systematic compositionality.

Convergence and Implicit Bias of Gradient Descent on Continual Linear Classification

We study continual learning on multiple linear classification tasks by sequentially running gradient descent (GD) for a fixed budget of iterations per task. When all tasks are jointly linearly separable and are presented in a cyclic/random order, we show the directional convergence of the trained linear classifier to the joint (offline) max-margin solution. This is surprising because GD training on a single task is implicitly biased towards the individual max-margin solution for the task, and the direction of the joint max-margin solution can be largely different from these individual solutions. Additionally, when tasks are given in a cyclic order, we present a non-asymptotic analysis on cycle-averaged forgetting, revealing that (1) alignment between tasks is indeed closely tied to catastrophic forgetting and backward knowledge transfer and (2) the amount of forgetting vanishes to zero as the cycle repeats. Lastly, we analyze the case where the tasks are no longer jointly separable and show that the model trained in a cyclic order converges to the unique minimum of the joint loss function.

DASH: Warm-Starting Neural Network Training in Stationary Settings without Loss of Plasticity

Warm-starting neural network training by initializing networks with previously learned weights is appealing, as practical neural networks are often deployed under a continuous influx of new data. However, it often leads to loss of plasticity, where the network loses its ability to learn new information, resulting in worse generalization than training from scratch. This occurs even under stationary data distributions, and its underlying mechanism is poorly understood. We develop a framework emulating real-world neural network training and identify noise memorization as the primary cause of plasticity loss when warm-starting on stationary data. Motivated by this, we propose Direction-Aware SHrinking (DASH), a method aiming to mitigate plasticity loss by selectively forgetting memorized noise while preserving learned features. e validate our approach on vision tasks, demonstrating improvements in test accuracy and training efficiency.

Arithmetic Transformers Can Length-Generalize in Both Operand Length and Count

Transformers often struggle with length generalization, meaning they fail to generalize to sequences longer than those encountered during training. While arithmetic tasks are commonly used to study length generalization, certain tasks are considered notoriously difficult, e.g., multi-operand addition (requiring generalization over both the number of operands and their lengths) and multiplication (requiring generalization over both operand lengths). In this work, we achieve approximately 2-3x length generalization on both tasks, which is the first such achievement in arithmetic Transformers. We design task-specific scratchpads enabling the model to focus on a fixed number of tokens per each next-token prediction step, and apply multi-level versions of Position Coupling (Cho et al., 2024; McLeish et al., 2024) to let Transformers know the right position to attend to. On the theory side, we prove that a 1-layer Transformer using our method can solve multi-operand addition, up to operand length and operand count that are exponential in embedding dimension.

Position Coupling: Leveraging Task Structure for Improved Length Generalization of Transformers

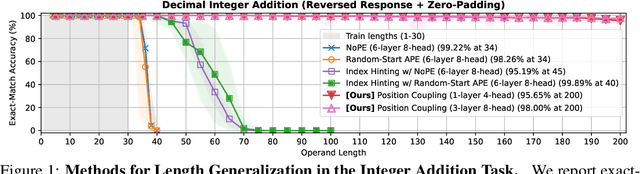
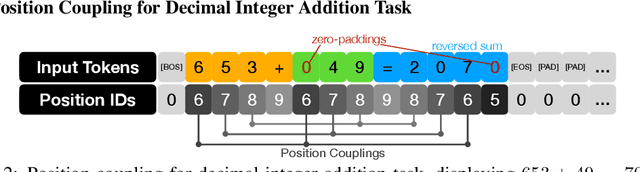
Even for simple arithmetic tasks like integer addition, it is challenging for Transformers to generalize to longer sequences than those encountered during training. To tackle this problem, we propose position coupling, a simple yet effective method that directly embeds the structure of the tasks into the positional encoding of a (decoder-only) Transformer. Taking a departure from the vanilla absolute position mechanism assigning unique position IDs to each of the tokens, we assign the same position IDs to two or more "relevant" tokens; for integer addition tasks, we regard digits of the same significance as in the same position. On the empirical side, we show that with the proposed position coupling, a small (1-layer) Transformer trained on 1 to 30-digit additions can generalize up to 200-digit additions (6.67x of the trained length). On the theoretical side, we prove that a 1-layer Transformer with coupled positions can solve the addition task involving exponentially many digits, whereas any 1-layer Transformer without positional information cannot entirely solve it. We also demonstrate that position coupling can be applied to other algorithmic tasks such as addition with multiple summands, Nx2 multiplication, copy/reverse, and a two-dimensional task.

Fundamental Benefit of Alternating Updates in Minimax Optimization

The Gradient Descent-Ascent (GDA) algorithm, designed to solve minimax optimization problems, takes the descent and ascent steps either simultaneously (Sim-GDA) or alternately (Alt-GDA). While Alt-GDA is commonly observed to converge faster, the performance gap between the two is not yet well understood theoretically, especially in terms of global convergence rates. To address this theory-practice gap, we present fine-grained convergence analyses of both algorithms for strongly-convex-strongly-concave and Lipschitz-gradient objectives. Our new iteration complexity upper bound of Alt-GDA is strictly smaller than the lower bound of Sim-GDA; i.e., Alt-GDA is provably faster. Moreover, we propose Alternating-Extrapolation GDA (Alex-GDA), a general algorithmic framework that subsumes Sim-GDA and Alt-GDA, for which the main idea is to alternately take gradients from extrapolations of the iterates. We show that Alex-GDA satisfies a smaller iteration complexity bound, identical to that of the Extra-gradient method, while requiring less gradient computations. We also prove that Alex-GDA enjoys linear convergence for bilinear problems, for which both Sim-GDA and Alt-GDA fail to converge at all.

Fair Streaming Principal Component Analysis: Statistical and Algorithmic Viewpoint

Fair Principal Component Analysis (PCA) is a problem setting where we aim to perform PCA while making the resulting representation fair in that the projected distributions, conditional on the sensitive attributes, match one another. However, existing approaches to fair PCA have two main problems: theoretically, there has been no statistical foundation of fair PCA in terms of learnability; practically, limited memory prevents us from using existing approaches, as they explicitly rely on full access to the entire data. On the theoretical side, we rigorously formulate fair PCA using a new notion called \emph{probably approximately fair and optimal} (PAFO) learnability. On the practical side, motivated by recent advances in streaming algorithms for addressing memory limitation, we propose a new setting called \emph{fair streaming PCA} along with a memory-efficient algorithm, fair noisy power method (FNPM). We then provide its {\it statistical} guarantee in terms of PAFO-learnability, which is the first of its kind in fair PCA literature. Lastly, we verify the efficacy and memory efficiency of our algorithm on real-world datasets.

Enhancing Generalization and Plasticity for Sample Efficient Reinforcement Learning

In Reinforcement Learning (RL), enhancing sample efficiency is crucial, particularly in scenarios when data acquisition is costly and risky. In principle, off-policy RL algorithms can improve sample efficiency by allowing multiple updates per environment interaction. However, these multiple updates often lead to overfitting, which decreases the network's ability to adapt to new data. We conduct an empirical analysis of this challenge and find that generalizability and plasticity constitute different roles in improving the model's adaptability. In response, we propose a combined usage of Sharpness-Aware Minimization (SAM) and a reset mechanism. SAM seeks wide, smooth minima, improving generalization, while the reset mechanism, through periodic reinitialization of the last few layers, consistently injects plasticity into the model. Through extensive empirical studies, we demonstrate that this combined usage improves sample efficiency and computational cost on the Atari-100k and DeepMind Control Suite benchmarks.

SGDA with shuffling: faster convergence for nonconvex-PŁ minimax optimization

Stochastic gradient descent-ascent (SGDA) is one of the main workhorses for solving finite-sum minimax optimization problems. Most practical implementations of SGDA randomly reshuffle components and sequentially use them (i.e., without-replacement sampling); however, there are few theoretical results on this approach for minimax algorithms, especially outside the easier-to-analyze (strongly-)monotone setups. To narrow this gap, we study the convergence bounds of SGDA with random reshuffling (SGDA-RR) for smooth nonconvex-nonconcave objectives with Polyak-{\L}ojasiewicz (P{\L}) geometry. We analyze both simultaneous and alternating SGDA-RR for nonconvex-P{\L} and primal-P{\L}-P{\L} objectives, and obtain convergence rates faster than with-replacement SGDA. Our rates also extend to mini-batch SGDA-RR, recovering known rates for full-batch gradient descent-ascent (GDA). Lastly, we present a comprehensive lower bound for two-time-scale GDA, which matches the full-batch rate for primal-P{\L}-P{\L} case.