Regularized Online RLHF with Generalized Bilinear Preferences

We consider the problem of contextual online RLHF with general preferences, where the goal is to identify the Nash Equilibrium. We adopt the Generalized Bilinear Preference Model (GBPM) to capture potentially intransitive preferences via low-rank, skew-symmetric matrices. We investigate general preference learning with any strongly convex regularizer (where $η^{-1}$ is the regularization strength), generalizing beyond prior works limited to reverse KL-regularization. Central to our analysis is proving that the dual gap of the greedy policy is bounded by the square of the estimation error - a result derived solely from strong convexity and the skew-symmetricity of GBPM.Building on this insight and a feature diversity assumption, we establish two regret bounds via two simple algorithms: (1) Greedy Sampling achieves polylogarithmic, $e^{O(η)}$-free regret $\tilde{O}(ηd^4 (\log T)^2)$. (2) Explore-Then-Commit achieves $\mathrm{poly}(d)$-free regret $\tilde{O}(\sqrt{ηr T})$ by exploiting the low-rank structure; this is the first statistically efficient guarantee for online RLHF in high-dimensions.

A Jointly Efficient and Optimal Algorithm for Heteroskedastic Generalized Linear Bandits with Adversarial Corruptions

We consider the problem of heteroskedastic generalized linear bandits (GLBs) with adversarial corruptions, which subsumes various stochastic contextual bandit settings, including heteroskedastic linear bandits and logistic/Poisson bandits. We propose HCW-GLB-OMD, which consists of two components: an online mirror descent (OMD)-based estimator and Hessian-based confidence weights to achieve corruption robustness. This is computationally efficient in that it only requires ${O}(1)$ space and time complexity per iteration. Under the self-concordance assumption on the link function, we show a regret bound of $\tilde{O}\left( d \sqrt{\sum_t g(τ_t) \dotμ_{t,\star}} + d^2 g_{\max} κ+ d κC \right)$, where $\dotμ_{t,\star}$ is the slope of $μ$ around the optimal arm at time $t$, $g(τ_t)$'s are potentially exogenously time-varying dispersions (e.g., $g(τ_t) = σ_t^2$ for heteroskedastic linear bandits, $g(τ_t) = 1$ for Bernoulli and Poisson), $g_{\max} = \max_{t \in [T]} g(τ_t)$ is the maximum dispersion, and $C \geq 0$ is the total corruption budget of the adversary. We complement this with a lower bound of $\tildeΩ(d \sqrt{\sum_t g(τ_t) \dotμ_{t,\star}} + d C)$, unifying previous problem-specific lower bounds. Thus, our algorithm achieves, up to a $κ$-factor in the corruption term, instance-wise minimax optimality simultaneously across various instances of heteroskedastic GLBs with adversarial corruptions.

Learning to Reason in LLMs by Expectation Maximization

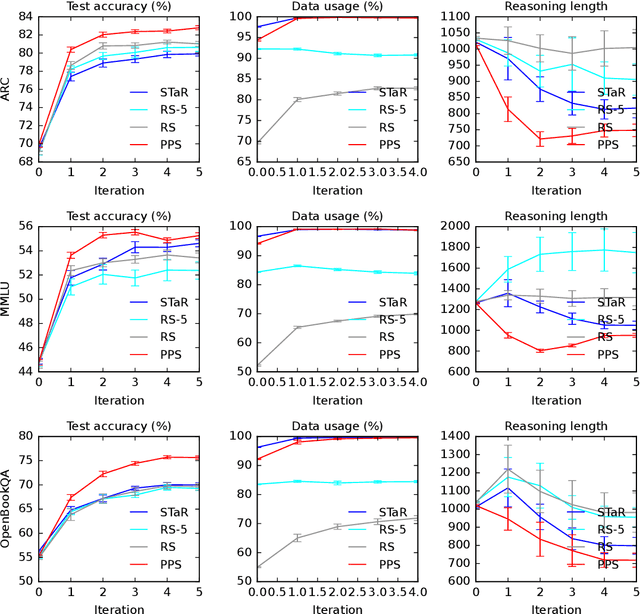
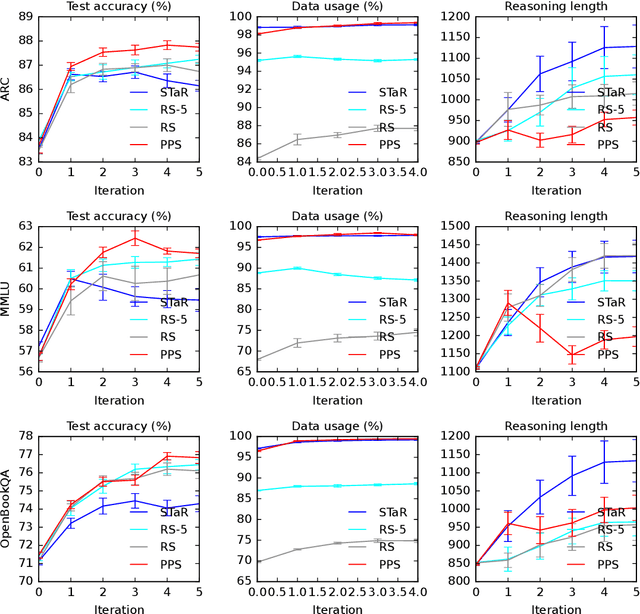
Large language models (LLMs) solve reasoning problems by first generating a rationale and then answering. We formalize reasoning as a latent variable model and derive an expectation-maximization (EM) objective for learning to reason. This view connects EM and modern reward-based optimization, and shows that the main challenge lies in designing a sampling distribution that generates rationales that justify correct answers. We instantiate and compare several sampling schemes: rejection sampling with a budget, self-taught reasoner (STaR), and prompt posterior sampling (PPS), which only keeps the rationalization stage of STaR. Our experiments on the ARC, MMLU, and OpenBookQA datasets with the Llama and Qwen models show that the sampling scheme can significantly affect the accuracy of learned reasoning models. Despite its simplicity, we observe that PPS outperforms the other sampling schemes.

AdaSTaR: Adaptive Data Sampling for Training Self-Taught Reasoners

Self-Taught Reasoners (STaR), synonymously known as Rejection sampling Fine-Tuning (RFT), is an integral part of the training pipeline of self-improving reasoning Language Models (LMs). The self-improving mechanism often employs random observation (data) sampling. However, this results in trained observation imbalance; inefficiently over-training on solved examples while under-training on challenging ones. In response, we introduce Adaptive STaR (AdaSTaR), a novel algorithm that rectifies this by integrating two adaptive sampling principles: (1) Adaptive Sampling for Diversity: promoting balanced training across observations, and (2) Adaptive Sampling for Curriculum: dynamically adjusting data difficulty to match the model's evolving strength. Across six benchmarks, AdaSTaR achieves best test accuracy in all instances (6/6) and reduces training FLOPs by an average of 58.6% against an extensive list of baselines. These improvements in performance and efficiency generalize to different pre-trained LMs and larger models, paving the way for more efficient and effective self-improving LMs.

Probability-Flow ODE in Infinite-Dimensional Function Spaces

Recent advances in infinite-dimensional diffusion models have demonstrated their effectiveness and scalability in function generation tasks where the underlying structure is inherently infinite-dimensional. To accelerate inference in such models, we derive, for the first time, an analog of the probability-flow ODE (PF-ODE) in infinite-dimensional function spaces. Leveraging this newly formulated PF-ODE, we reduce the number of function evaluations while maintaining sample quality in function generation tasks, including applications to PDEs.

FlickerFusion: Intra-trajectory Domain Generalizing Multi-Agent RL

Multi-agent reinforcement learning has demonstrated significant potential in addressing complex cooperative tasks across various real-world applications. However, existing MARL approaches often rely on the restrictive assumption that the number of entities (e.g., agents, obstacles) remains constant between training and inference. This overlooks scenarios where entities are dynamically removed or added during the inference trajectory -- a common occurrence in real-world environments like search and rescue missions and dynamic combat situations. In this paper, we tackle the challenge of intra-trajectory dynamic entity composition under zero-shot out-of-domain (OOD) generalization, where such dynamic changes cannot be anticipated beforehand. Our empirical studies reveal that existing MARL methods suffer significant performance degradation and increased uncertainty in these scenarios. In response, we propose FlickerFusion, a novel OOD generalization method that acts as a universally applicable augmentation technique for MARL backbone methods. Our results show that FlickerFusion not only achieves superior inference rewards but also uniquely reduces uncertainty vis-\`a-vis the backbone, compared to existing methods. For standardized evaluation, we introduce MPEv2, an enhanced version of Multi Particle Environments (MPE), consisting of 12 benchmarks. Benchmarks, implementations, and trained models are organized and open-sourced at flickerfusion305.github.io, accompanied by ample demo video renderings.

A Unified Confidence Sequence for Generalized Linear Models, with Applications to Bandits

We present a unified likelihood ratio-based confidence sequence (CS) for any (self-concordant) generalized linear models (GLMs) that is guaranteed to be convex and numerically tight. We show that this is on par or improves upon known CSs for various GLMs, including Gaussian, Bernoulli, and Poisson. In particular, for the first time, our CS for Bernoulli has a poly(S)-free radius where S is the norm of the unknown parameter. Our first technical novelty is its derivation, which utilizes a time-uniform PAC-Bayesian bound with a uniform prior/posterior, despite the latter being a rather unpopular choice for deriving CSs. As a direct application of our new CS, we propose a simple and natural optimistic algorithm called OFUGLB applicable to any generalized linear bandits (GLB; Filippi et al. (2010)). Our analysis shows that the celebrated optimistic approach simultaneously attains state-of-the-art regrets for various self-concordant (not necessarily bounded) GLBs, and even poly(S)-free for bounded GLBs, including logistic bandits. The regret analysis, our second technical novelty, follows from combining our new CS with a new proof technique that completely avoids the previously widely used self-concordant control lemma (Faury et al., 2020, Lemma 9). Finally, we verify numerically that OFUGLB significantly outperforms the prior state-of-the-art (Lee et al., 2024) for logistic bandits.

Querying Easily Flip-flopped Samples for Deep Active Learning

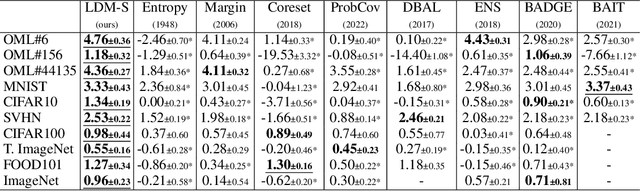
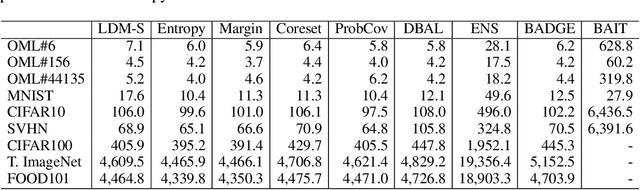
Active learning is a machine learning paradigm that aims to improve the performance of a model by strategically selecting and querying unlabeled data. One effective selection strategy is to base it on the model's predictive uncertainty, which can be interpreted as a measure of how informative a sample is. The sample's distance to the decision boundary is a natural measure of predictive uncertainty, but it is often intractable to compute, especially for complex decision boundaries formed in multiclass classification tasks. To address this issue, this paper proposes the {\it least disagree metric} (LDM), defined as the smallest probability of disagreement of the predicted label, and an estimator for LDM proven to be asymptotically consistent under mild assumptions. The estimator is computationally efficient and can be easily implemented for deep learning models using parameter perturbation. The LDM-based active learning is performed by querying unlabeled data with the smallest LDM. Experimental results show that our LDM-based active learning algorithm obtains state-of-the-art overall performance on all considered datasets and deep architectures.

Large Catapults in Momentum Gradient Descent with Warmup: An Empirical Study

Although gradient descent with momentum is widely used in modern deep learning, a concrete understanding of its effects on the training trajectory still remains elusive. In this work, we empirically show that momentum gradient descent with a large learning rate and learning rate warmup displays large catapults, driving the iterates towards flatter minima than those found by gradient descent. We then provide empirical evidence and theoretical intuition that the large catapult is caused by momentum "amplifying" the self-stabilization effect (Damian et al., 2023).

Fair Streaming Principal Component Analysis: Statistical and Algorithmic Viewpoint

Fair Principal Component Analysis (PCA) is a problem setting where we aim to perform PCA while making the resulting representation fair in that the projected distributions, conditional on the sensitive attributes, match one another. However, existing approaches to fair PCA have two main problems: theoretically, there has been no statistical foundation of fair PCA in terms of learnability; practically, limited memory prevents us from using existing approaches, as they explicitly rely on full access to the entire data. On the theoretical side, we rigorously formulate fair PCA using a new notion called \emph{probably approximately fair and optimal} (PAFO) learnability. On the practical side, motivated by recent advances in streaming algorithms for addressing memory limitation, we propose a new setting called \emph{fair streaming PCA} along with a memory-efficient algorithm, fair noisy power method (FNPM). We then provide its {\it statistical} guarantee in terms of PAFO-learnability, which is the first of its kind in fair PCA literature. Lastly, we verify the efficacy and memory efficiency of our algorithm on real-world datasets.