Neural Window Decoder for SC-LDPC Codes

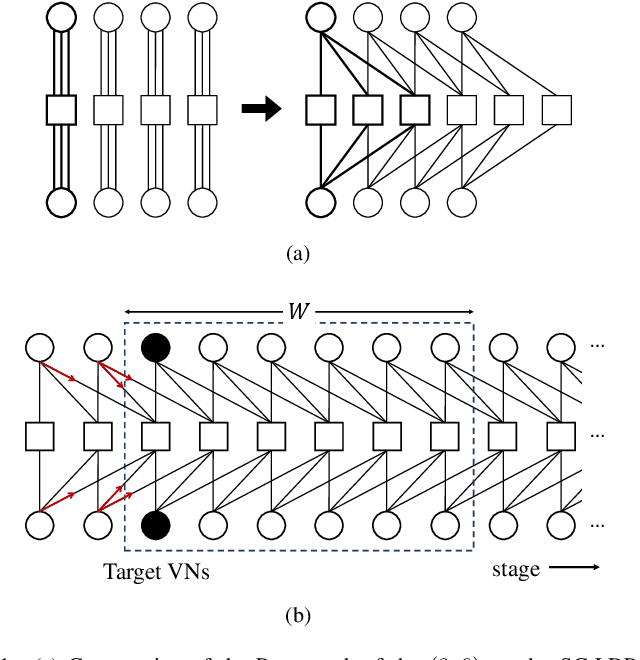
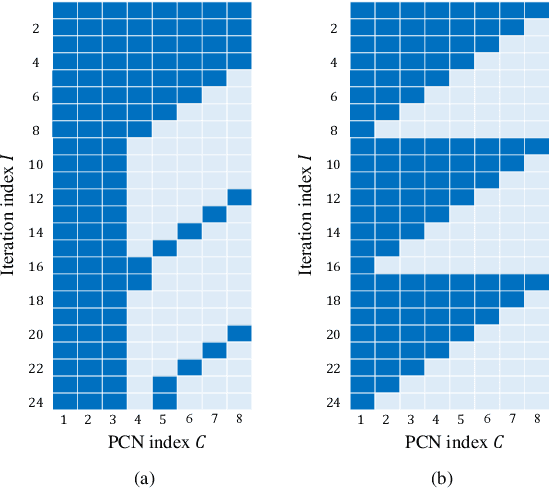
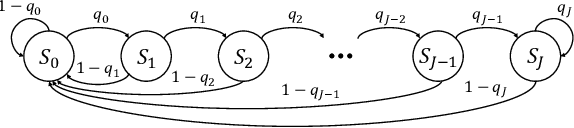
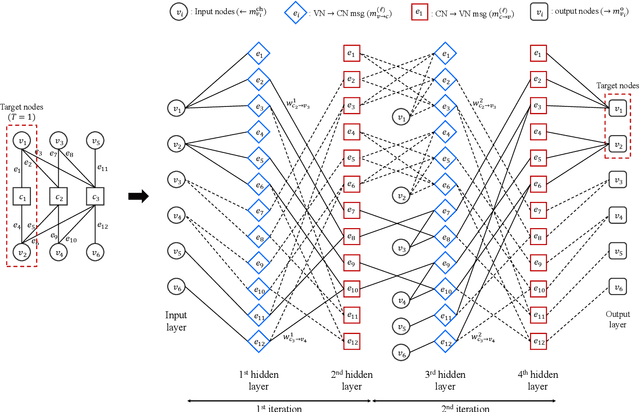
In this paper, we propose a neural window decoder (NWD) for spatially coupled low-density parity-check (SC-LDPC) codes. The proposed NWD retains the conventional window decoder (WD) process but incorporates trainable neural weights. To train the weights of NWD, we introduce two novel training strategies. First, we restrict the loss function to target variable nodes (VNs) of the window, which prunes the neural network and accordingly enhances training efficiency. Second, we employ the active learning technique with a normalized loss term to prevent the training process from biasing toward specific training regions. Next, we develop a systematic method to derive non-uniform schedules for the NWD based on the training results. We introduce trainable damping factors that reflect the relative importance of check node (CN) updates. By skipping updates with less importance, we can omit $\mathbf{41\%}$ of CN updates without performance degradation compared to the conventional WD. Lastly, we address the error propagation problem inherent in SC-LDPC codes by deploying a complementary weight set, which is activated when an error is detected in the previous window. This adaptive decoding strategy effectively mitigates error propagation without requiring modifications to the code and decoder structures.

Boosted Neural Decoders: Achieving Extreme Reliability of LDPC Codes for 6G Networks

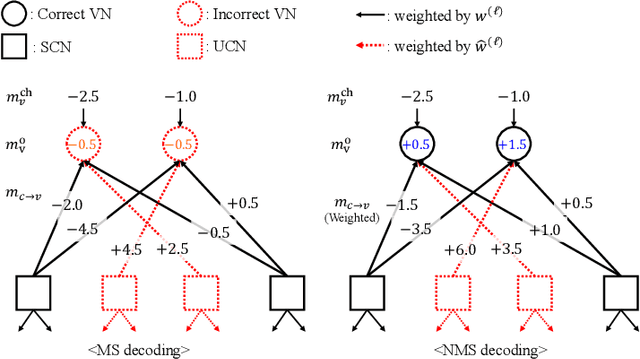
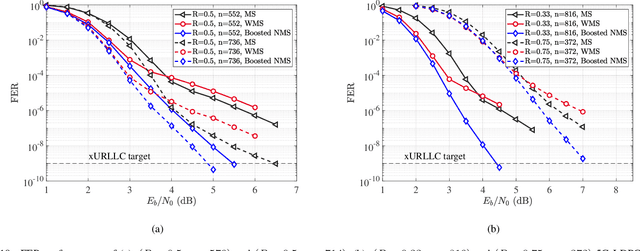
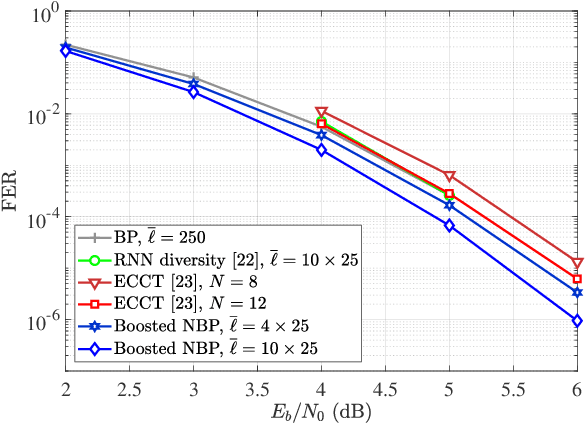
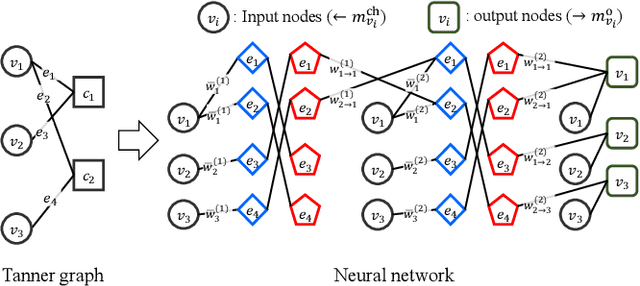
Ensuring extremely high reliability is essential for channel coding in 6G networks. The next-generation of ultra-reliable and low-latency communications (xURLLC) scenario within 6G networks requires a frame error rate (FER) below 10-9. However, low-density parity-check (LDPC) codes, the standard in 5G new radio (NR), encounter a challenge known as the error floor phenomenon, which hinders to achieve such low rates. To tackle this problem, we introduce an innovative solution: boosted neural min-sum (NMS) decoder. This decoder operates identically to conventional NMS decoders, but is trained by novel training methods including: i) boosting learning with uncorrected vectors, ii) block-wise training schedule to address the vanishing gradient issue, iii) dynamic weight sharing to minimize the number of trainable weights, iv) transfer learning to reduce the required sample count, and v) data augmentation to expedite the sampling process. Leveraging these training strategies, the boosted NMS decoder achieves the state-of-the art performance in reducing the error floor as well as superior waterfall performance. Remarkably, we fulfill the 6G xURLLC requirement for 5G LDPC codes without the severe error floor. Additionally, the boosted NMS decoder, once its weights are trained, can perform decoding without additional modules, making it highly practical for immediate application.

CrossMPT: Cross-attention Message-Passing Transformer for Error Correcting Codes

Error correcting codes~(ECCs) are indispensable for reliable transmission in communication systems. The recent advancements in deep learning have catalyzed the exploration of ECC decoders based on neural networks. Among these, transformer-based neural decoders have achieved state-of-the-art decoding performance. In this paper, we propose a novel Cross-attention Message-Passing Transformer~(CrossMPT). CrossMPT iteratively updates two types of input vectors (i.e., magnitude and syndrome vectors) using two masked cross-attention blocks. The mask matrices in these cross-attention blocks are determined by the code's parity-check matrix that delineates the relationship between magnitude and syndrome vectors. Our experimental results show that CrossMPT significantly outperforms existing neural network-based decoders, particularly in decoding low-density parity-check codes. Notably, CrossMPT also achieves a significant reduction in computational complexity, achieving over a 50\% decrease in its attention layers compared to the original transformer-based decoder, while retaining the computational complexity of the remaining layers.

Optimizing Layerwise Polynomial Approximation for Efficient Private Inference on Fully Homomorphic Encryption: A Dynamic Programming Approach

Recent research has explored the implementation of privacy-preserving deep neural networks solely using fully homomorphic encryption. However, its practicality has been limited because of prolonged inference times. When using a pre-trained model without retraining, a major factor contributing to these prolonged inference times is the high-degree polynomial approximation of activation functions such as the ReLU function. The high-degree approximation consumes a substantial amount of homomorphic computational resources, resulting in slower inference. Unlike the previous works approximating activation functions uniformly and conservatively, this paper presents a \emph{layerwise} degree optimization of activation functions to aggressively reduce the inference time while maintaining classification accuracy by taking into account the characteristics of each layer. Instead of the minimax approximation commonly used in state-of-the-art private inference models, we employ the weighted least squares approximation method with the input distributions of activation functions. Then, we obtain the layerwise optimized degrees for activation functions through the \emph{dynamic programming} algorithm, considering how each layer's approximation error affects the classification accuracy of the deep neural network. Furthermore, we propose modulating the ciphertext moduli-chain layerwise to reduce the inference time. By these proposed layerwise optimization methods, we can reduce inference times for the ResNet-20 model and the ResNet-32 model by 3.44 times and 3.16 times, respectively, in comparison to the prior implementations employing uniform degree polynomials and a consistent ciphertext modulus.

Boosting Learning for LDPC Codes to Improve the Error-Floor Performance

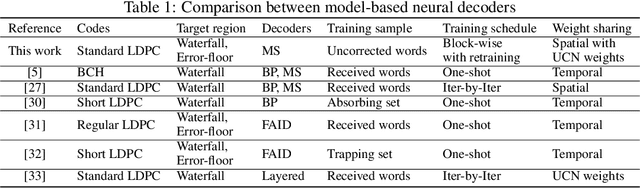
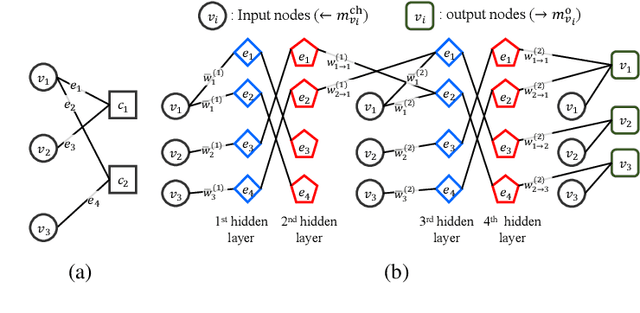
Low-density parity-check (LDPC) codes have been successfully commercialized in communication systems due to their strong error correction ability and simple decoding process. However, the error-floor phenomenon of LDPC codes, in which the error rate stops decreasing rapidly at a certain level, poses challenges in achieving extremely low error rates and the application of LDPC codes in scenarios demanding ultra high reliability. In this work, we propose training methods to optimize neural min-sum (NMS) decoders that are robust to the error-floor. Firstly, by leveraging the boosting learning technique of ensemble networks, we divide the decoding network into two networks and train the post network to be specialized for uncorrected codewords that failed in the first network. Secondly, to address the vanishing gradient issue in training, we introduce a block-wise training schedule that locally trains a block of weights while retraining the preceding block. Lastly, we show that assigning different weights to unsatisfied check nodes effectively lowers the error-floor with a minimal number of weights. By applying these training methods to standard LDPC codes, we achieve the best error-floor performance compared to other decoding methods. The proposed NMS decoder, optimized solely through novel training methods without additional modules, can be implemented into current LDPC decoders without incurring extra hardware costs. The source code is available at https://github.com/ghy1228/LDPC_Error_Floor.

How to Mask in Error Correction Code Transformer: Systematic and Double Masking

In communication and storage systems, error correction codes (ECCs) are pivotal in ensuring data reliability. As deep learning's applicability has broadened across diverse domains, there is a growing research focus on neural network-based decoders that outperform traditional decoding algorithms. Among these neural decoders, Error Correction Code Transformer (ECCT) has achieved the state-of-the-art performance, outperforming other methods by large margins. To further enhance the performance of ECCT, we propose two novel methods. First, leveraging the systematic encoding technique of ECCs, we introduce a new masking matrix for ECCT, aiming to improve the performance and reduce the computational complexity. Second, we propose a novel transformer architecture of ECCT called a double-masked ECCT. This architecture employs two different mask matrices in a parallel manner to learn more diverse features of the relationship between codeword bits in the masked self-attention blocks. Extensive simulation results show that the proposed double-masked ECCT outperforms the conventional ECCT, achieving the state-of-the-art decoding performance with significant margins.

Privacy-Preserving Machine Learning with Fully Homomorphic Encryption for Deep Neural Network

Fully homomorphic encryption (FHE) is one of the prospective tools for privacypreserving machine learning (PPML), and several PPML models have been proposed based on various FHE schemes and approaches. Although the FHE schemes are known as suitable tools to implement PPML models, previous PPML models on FHE encrypted data are limited to only simple and non-standard types of machine learning models. These non-standard machine learning models are not proven efficient and accurate with more practical and advanced datasets. Previous PPML schemes replace non-arithmetic activation functions with simple arithmetic functions instead of adopting approximation methods and do not use bootstrapping, which enables continuous homomorphic evaluations. Thus, they could not use standard activation functions and could not employ a large number of layers. The maximum classification accuracy of the existing PPML model with the FHE for the CIFAR-10 dataset was only 77% until now. In this work, we firstly implement the standard ResNet-20 model with the RNS-CKKS FHE with bootstrapping and verify the implemented model with the CIFAR-10 dataset and the plaintext model parameters. Instead of replacing the non-arithmetic functions with the simple arithmetic function, we use state-of-the-art approximation methods to evaluate these non-arithmetic functions, such as the ReLU, with sufficient precision [1]. Further, for the first time, we use the bootstrapping technique of the RNS-CKKS scheme in the proposed model, which enables us to evaluate a deep learning model on the encrypted data. We numerically verify that the proposed model with the CIFAR-10 dataset shows 98.67% identical results to the original ResNet-20 model with non-encrypted data. The classification accuracy of the proposed model is 90.67%, which is pretty close to that of the original ResNet-20 CNN model...

Weakly Private Information Retrieval Under Rényi Divergence

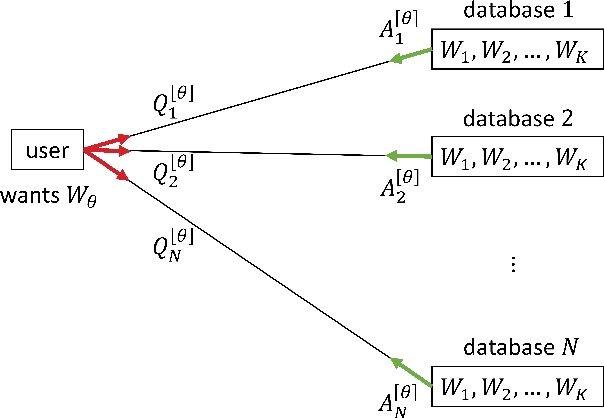
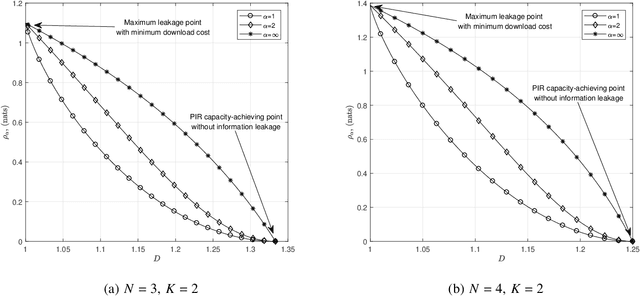
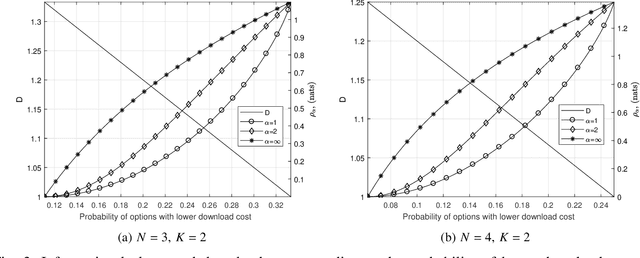
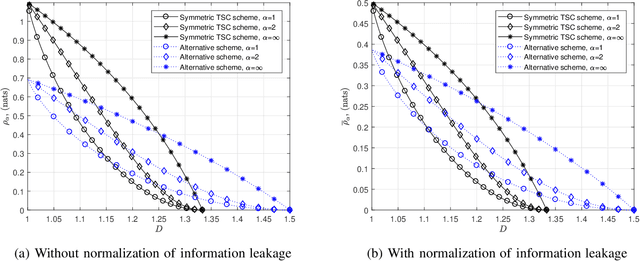
Private information retrieval (PIR) is a protocol that guarantees the privacy of a user who is in communication with databases. The user wants to download one of the messages stored in the databases while hiding the identity of the desired message. Recently, the benefits that can be obtained by weakening the privacy requirement have been studied, but the definition of weak privacy needs to be elaborated upon. In this paper, we attempt to quantify the weak privacy (i.e., information leakage) in PIR problems by using the R\'enyi divergence that generalizes the Kullback-Leibler divergence. By introducing R\'enyi divergence into the existing PIR problem, the tradeoff relationship between privacy (information leakage) and PIR performance (download cost) is characterized via convex optimization. Furthermore, we propose an alternative PIR scheme with smaller message sizes than the Tian-Sun-Chen (TSC) scheme. The proposed scheme cannot achieve the PIR capacity of perfect privacy since the message size of the TSC scheme is the minimum to achieve the PIR capacity. However, we show that the proposed scheme can be better than the TSC scheme in the weakly PIR setting, especially under a low download cost regime.

Iterative DNA Coding Scheme With GC Balance and Run-Length Constraints Using a Greedy Algorithm

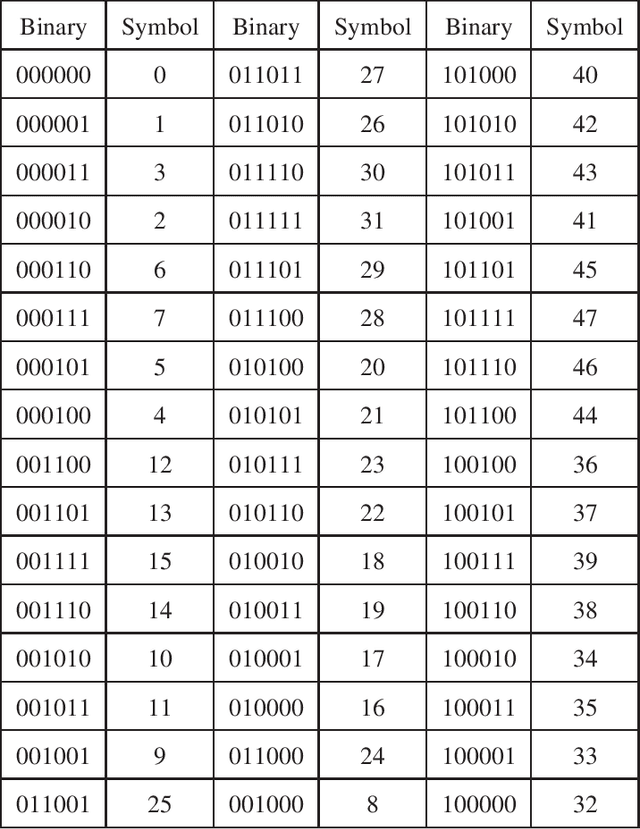
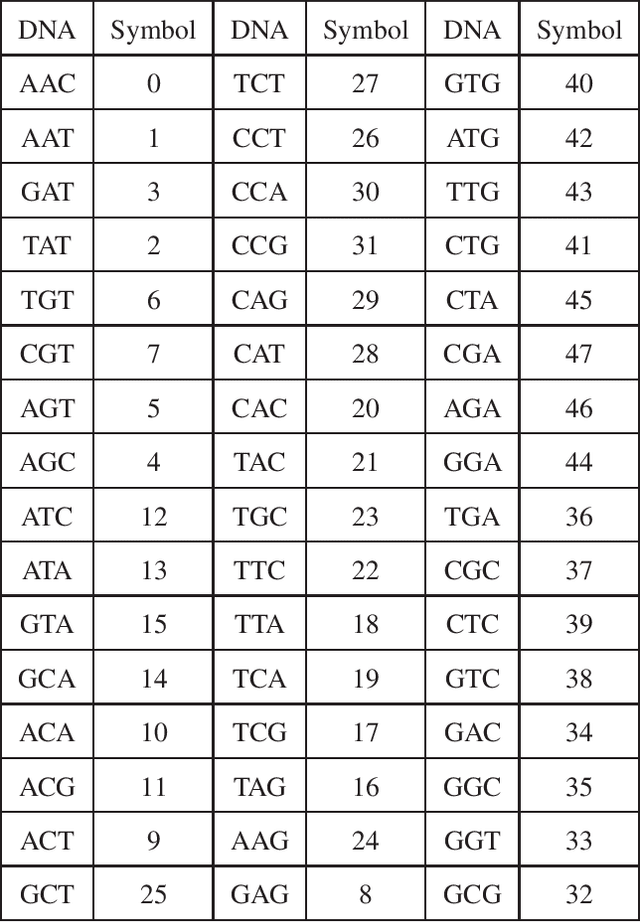
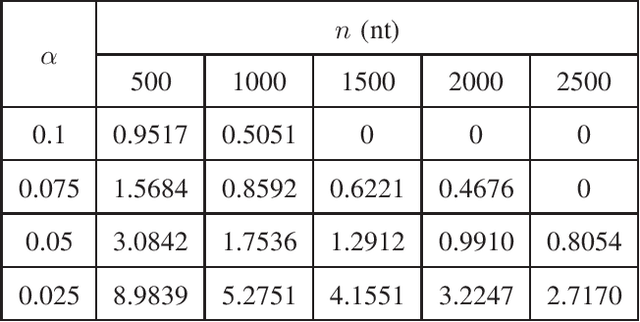
In this paper, we propose a novel iterative encoding algorithm for DNA storage to satisfy both the GC balance and run-length constraints using a greedy algorithm. DNA strands with run-length more than three and the GC balance ratio far from 50\% are known to be prone to errors. The proposed encoding algorithm stores data at high information density with high flexibility of run-length at most $m$ and GC balance between $0.5\pm\alpha$ for arbitrary $m$ and $\alpha$. More importantly, we propose a novel mapping method to reduce the average bit error compared to the randomly generated mapping method, using a greedy algorithm. The proposed algorithm is implemented through iterative encoding, consisting of three main steps: randomization, M-ary mapping, and verification. It has an information density of 1.8616 bits/nt in the case of $m=3$, which approaches the theoretical upper bound of 1.98 bits/nt, while satisfying two constraints. Also, the average bit error caused by the one nt error is 2.3455 bits, which is reduced by $20.5\%$, compared to the randomized mapping.