Iterative DNA Coding Scheme With GC Balance and Run-Length Constraints Using a Greedy Algorithm
Paper and Code
Mar 30, 2021
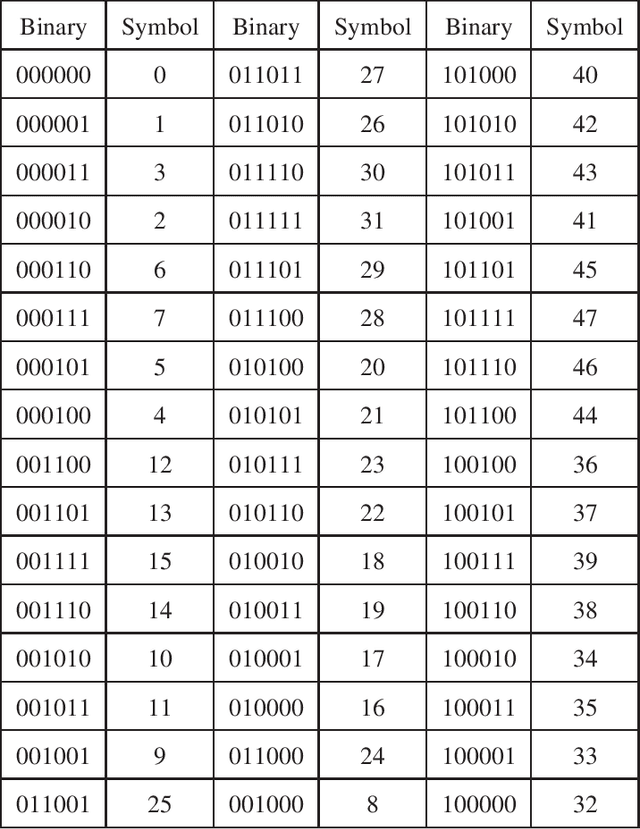
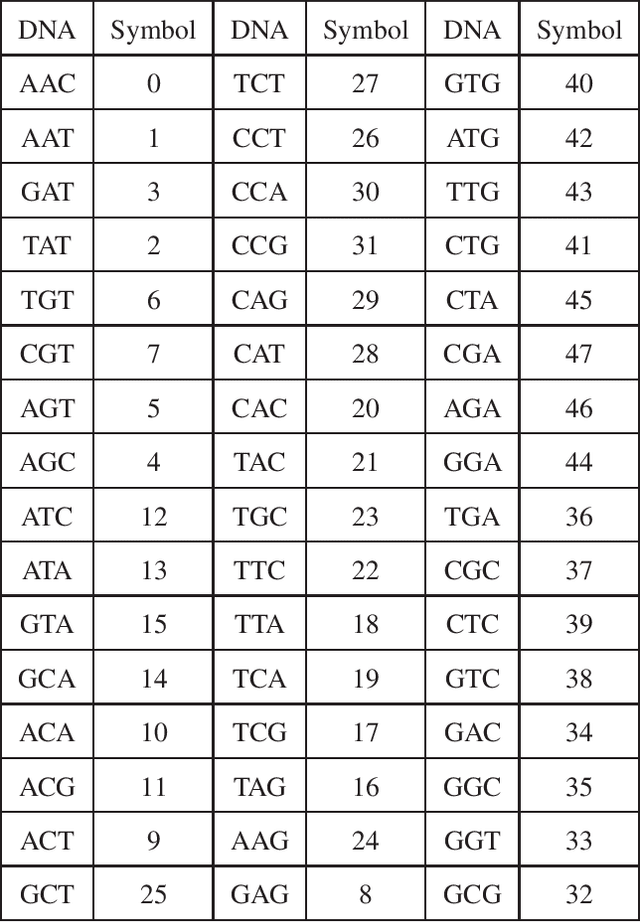
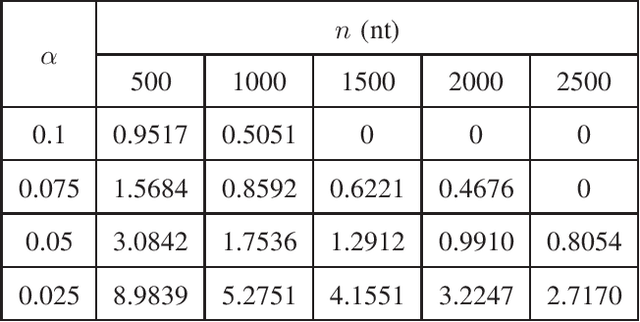
In this paper, we propose a novel iterative encoding algorithm for DNA storage to satisfy both the GC balance and run-length constraints using a greedy algorithm. DNA strands with run-length more than three and the GC balance ratio far from 50\% are known to be prone to errors. The proposed encoding algorithm stores data at high information density with high flexibility of run-length at most $m$ and GC balance between $0.5\pm\alpha$ for arbitrary $m$ and $\alpha$. More importantly, we propose a novel mapping method to reduce the average bit error compared to the randomly generated mapping method, using a greedy algorithm. The proposed algorithm is implemented through iterative encoding, consisting of three main steps: randomization, M-ary mapping, and verification. It has an information density of 1.8616 bits/nt in the case of $m=3$, which approaches the theoretical upper bound of 1.98 bits/nt, while satisfying two constraints. Also, the average bit error caused by the one nt error is 2.3455 bits, which is reduced by $20.5\%$, compared to the randomized mapping.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge