Weakly Private Information Retrieval Under Rényi Divergence
Paper and Code
May 17, 2021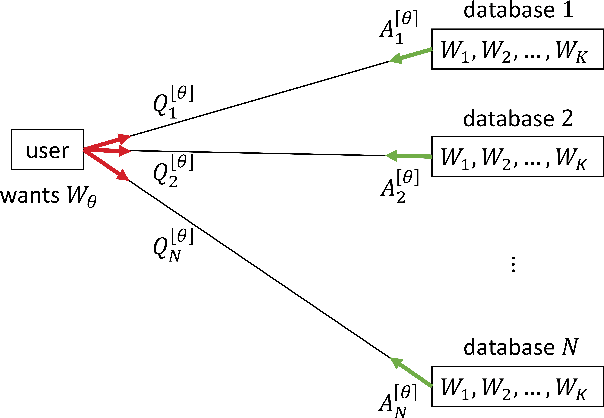
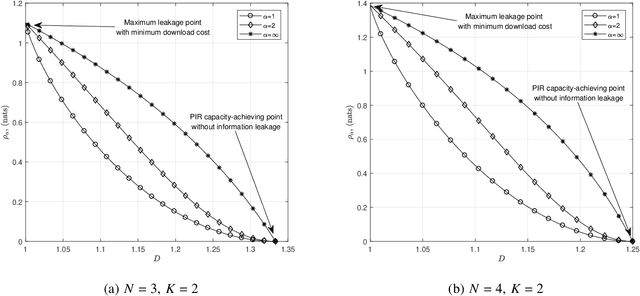
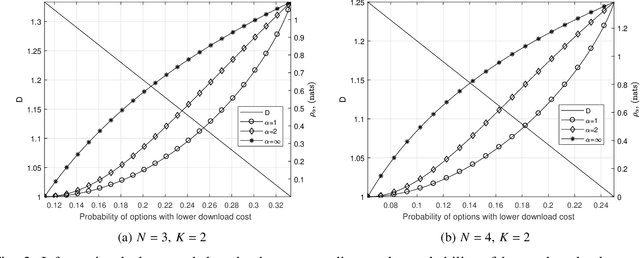
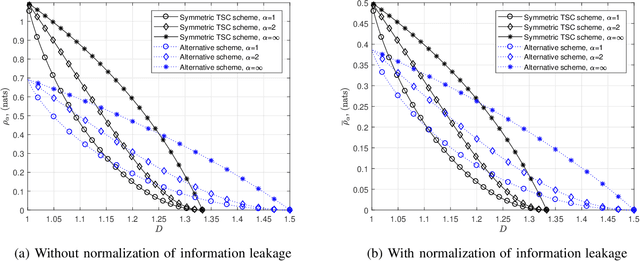
Private information retrieval (PIR) is a protocol that guarantees the privacy of a user who is in communication with databases. The user wants to download one of the messages stored in the databases while hiding the identity of the desired message. Recently, the benefits that can be obtained by weakening the privacy requirement have been studied, but the definition of weak privacy needs to be elaborated upon. In this paper, we attempt to quantify the weak privacy (i.e., information leakage) in PIR problems by using the R\'enyi divergence that generalizes the Kullback-Leibler divergence. By introducing R\'enyi divergence into the existing PIR problem, the tradeoff relationship between privacy (information leakage) and PIR performance (download cost) is characterized via convex optimization. Furthermore, we propose an alternative PIR scheme with smaller message sizes than the Tian-Sun-Chen (TSC) scheme. The proposed scheme cannot achieve the PIR capacity of perfect privacy since the message size of the TSC scheme is the minimum to achieve the PIR capacity. However, we show that the proposed scheme can be better than the TSC scheme in the weakly PIR setting, especially under a low download cost regime.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge