Spark Transformer: Reactivating Sparsity in FFN and Attention

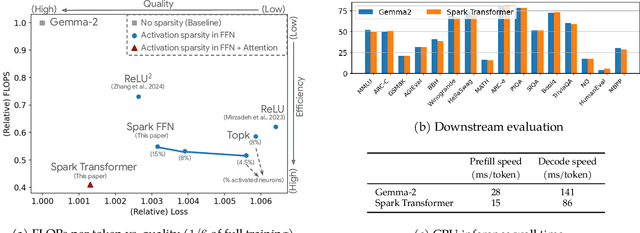
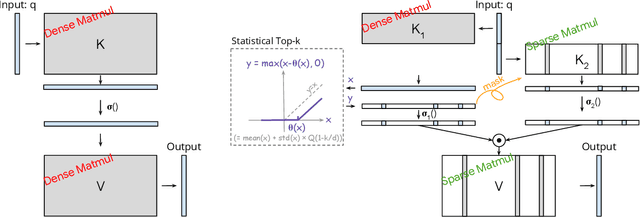
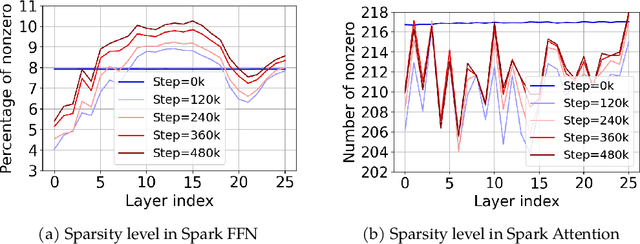
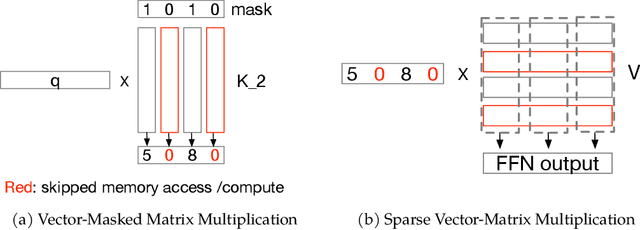
The discovery of the lazy neuron phenomenon in trained Transformers, where the vast majority of neurons in their feed-forward networks (FFN) are inactive for each token, has spurred tremendous interests in activation sparsity for enhancing large model efficiency. While notable progress has been made in translating such sparsity to wall-time benefits, modern Transformers have moved away from the ReLU activation function crucial to this phenomenon. Existing efforts on re-introducing activation sparsity often degrade model quality, increase parameter count, complicate or slow down training. Sparse attention, the application of sparse activation to the attention mechanism, often faces similar challenges. This paper introduces the Spark Transformer, a novel architecture that achieves a high level of activation sparsity in both FFN and the attention mechanism while maintaining model quality, parameter count, and standard training procedures. Our method realizes sparsity via top-k masking for explicit control over sparsity level. Crucially, we introduce statistical top-k, a hardware-accelerator-friendly, linear-time approximate algorithm that avoids costly sorting and mitigates significant training slowdown from standard top-$k$ operators. Furthermore, Spark Transformer reallocates existing FFN parameters and attention key embeddings to form a low-cost predictor for identifying activated entries. This design not only mitigates quality loss from enforced sparsity, but also enhances wall-time benefit. Pretrained with the Gemma-2 recipe, Spark Transformer demonstrates competitive performance on standard benchmarks while exhibiting significant sparsity: only 8% of FFN neurons are activated, and each token attends to a maximum of 256 tokens. This sparsity translates to a 2.5x reduction in FLOPs, leading to decoding wall-time speedups of up to 1.79x on CPU and 1.40x on GPU.

Arithmetic Transformers Can Length-Generalize in Both Operand Length and Count

Transformers often struggle with length generalization, meaning they fail to generalize to sequences longer than those encountered during training. While arithmetic tasks are commonly used to study length generalization, certain tasks are considered notoriously difficult, e.g., multi-operand addition (requiring generalization over both the number of operands and their lengths) and multiplication (requiring generalization over both operand lengths). In this work, we achieve approximately 2-3x length generalization on both tasks, which is the first such achievement in arithmetic Transformers. We design task-specific scratchpads enabling the model to focus on a fixed number of tokens per each next-token prediction step, and apply multi-level versions of Position Coupling (Cho et al., 2024; McLeish et al., 2024) to let Transformers know the right position to attend to. On the theory side, we prove that a 1-layer Transformer using our method can solve multi-operand addition, up to operand length and operand count that are exponential in embedding dimension.

Mimetic Initialization Helps State Space Models Learn to Recall

Recent work has shown that state space models such as Mamba are significantly worse than Transformers on recall-based tasks due to the fact that their state size is constant with respect to their input sequence length. But in practice, state space models have fairly large state sizes, and we conjecture that they should be able to perform much better at these tasks than previously reported. We investigate whether their poor copying and recall performance could be due in part to training difficulties rather than fundamental capacity constraints. Based on observations of their "attention" maps, we propose a structured initialization technique that allows state space layers to more readily mimic attention. Across a variety of architecture settings, our initialization makes it substantially easier for Mamba to learn to copy and do associative recall from scratch.

Position Coupling: Leveraging Task Structure for Improved Length Generalization of Transformers

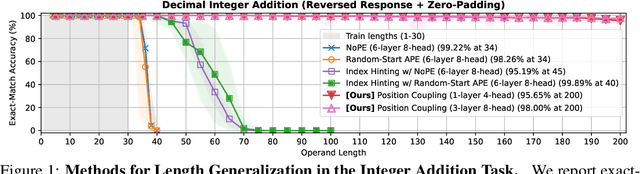
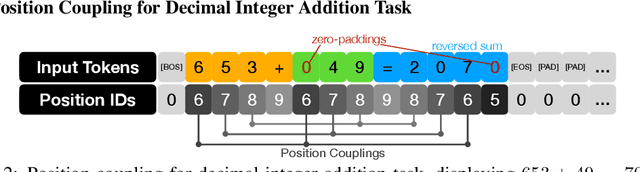
Even for simple arithmetic tasks like integer addition, it is challenging for Transformers to generalize to longer sequences than those encountered during training. To tackle this problem, we propose position coupling, a simple yet effective method that directly embeds the structure of the tasks into the positional encoding of a (decoder-only) Transformer. Taking a departure from the vanilla absolute position mechanism assigning unique position IDs to each of the tokens, we assign the same position IDs to two or more "relevant" tokens; for integer addition tasks, we regard digits of the same significance as in the same position. On the empirical side, we show that with the proposed position coupling, a small (1-layer) Transformer trained on 1 to 30-digit additions can generalize up to 200-digit additions (6.67x of the trained length). On the theoretical side, we prove that a 1-layer Transformer with coupled positions can solve the addition task involving exponentially many digits, whereas any 1-layer Transformer without positional information cannot entirely solve it. We also demonstrate that position coupling can be applied to other algorithmic tasks such as addition with multiple summands, Nx2 multiplication, copy/reverse, and a two-dimensional task.

Efficient Language Model Architectures for Differentially Private Federated Learning

Cross-device federated learning (FL) is a technique that trains a model on data distributed across typically millions of edge devices without data leaving the devices. SGD is the standard client optimizer for on device training in cross-device FL, favored for its memory and computational efficiency. However, in centralized training of neural language models, adaptive optimizers are preferred as they offer improved stability and performance. In light of this, we ask if language models can be modified such that they can be efficiently trained with SGD client optimizers and answer this affirmatively. We propose a scale-invariant Coupled Input Forget Gate (SI CIFG) recurrent network by modifying the sigmoid and tanh activations in the recurrent cell and show that this new model converges faster and achieves better utility than the standard CIFG recurrent model in cross-device FL in large scale experiments. We further show that the proposed scale invariant modification also helps in federated learning of larger transformer models. Finally, we demonstrate the scale invariant modification is also compatible with other non-adaptive algorithms. Particularly, our results suggest an improved privacy utility trade-off in federated learning with differential privacy.

HiRE: High Recall Approximate Top-$k$ Estimation for Efficient LLM Inference

Autoregressive decoding with generative Large Language Models (LLMs) on accelerators (GPUs/TPUs) is often memory-bound where most of the time is spent on transferring model parameters from high bandwidth memory (HBM) to cache. On the other hand, recent works show that LLMs can maintain quality with significant sparsity/redundancy in the feedforward (FFN) layers by appropriately training the model to operate on a top-$k$ fraction of rows/columns (where $k \approx 0.05$), there by suggesting a way to reduce the transfer of model parameters, and hence latency. However, exploiting this sparsity for improving latency is hindered by the fact that identifying top rows/columns is data-dependent and is usually performed using full matrix operations, severely limiting potential gains. To address these issues, we introduce HiRE (High Recall Approximate Top-k Estimation). HiRE comprises of two novel components: (i) a compression scheme to cheaply predict top-$k$ rows/columns with high recall, followed by full computation restricted to the predicted subset, and (ii) DA-TOP-$k$: an efficient multi-device approximate top-$k$ operator. We demonstrate that on a one billion parameter model, HiRE applied to both the softmax as well as feedforward layers, achieves almost matching pretraining and downstream accuracy, and speeds up inference latency by $1.47\times$ on a single TPUv5e device.

Efficacy of Dual-Encoders for Extreme Multi-Label Classification

Dual-encoder models have demonstrated significant success in dense retrieval tasks for open-domain question answering that mostly involves zero-shot and few-shot scenarios. However, their performance in many-shot retrieval problems where training data is abundant, such as extreme multi-label classification (XMC), remains under-explored. Existing empirical evidence suggests that, for such problems, the dual-encoder method's accuracies lag behind the performance of state-of-the-art (SOTA) extreme classification methods that grow the number of learnable parameters linearly with the number of classes. As a result, some recent extreme classification techniques use a combination of dual-encoders and a learnable classification head for each class to excel on these tasks. In this paper, we investigate the potential of "pure" DE models in XMC tasks. Our findings reveal that when trained correctly standard dual-encoders can match or outperform SOTA extreme classification methods by up to 2% at Precision@1 even on the largest XMC datasets while being 20x smaller in terms of the number of trainable parameters. We further propose a differentiable topk error-based loss function, which can be used to specifically optimize for Recall@k metrics. We include our PyTorch implementation along with other resources for reproducing the results in the supplementary material.

Functional Interpolation for Relative Positions Improves Long Context Transformers

Preventing the performance decay of Transformers on inputs longer than those used for training has been an important challenge in extending the context length of these models. Though the Transformer architecture has fundamentally no limits on the input sequence lengths it can process, the choice of position encoding used during training can limit the performance of these models on longer inputs. We propose a novel functional relative position encoding with progressive interpolation, FIRE, to improve Transformer generalization to longer contexts. We theoretically prove that this can represent some of the popular relative position encodings, such as T5's RPE, Alibi, and Kerple. We next empirically show that FIRE models have better generalization to longer contexts on both zero-shot language modeling and long text benchmarks.

Depth Dependence of $μ$P Learning Rates in ReLU MLPs

In this short note we consider random fully connected ReLU networks of width $n$ and depth $L$ equipped with a mean-field weight initialization. Our purpose is to study the dependence on $n$ and $L$ of the maximal update ($\mu$P) learning rate, the largest learning rate for which the mean squared change in pre-activations after one step of gradient descent remains uniformly bounded at large $n,L$. As in prior work on $\mu$P of Yang et. al., we find that this maximal update learning rate is independent of $n$ for all but the first and last layer weights. However, we find that it has a non-trivial dependence of $L$, scaling like $L^{-3/2}.$

On student-teacher deviations in distillation: does it pay to disobey?

Knowledge distillation has been widely-used to improve the performance of a "student" network by hoping to mimic soft probabilities of a "teacher" network. Yet, for self-distillation to work, the student must somehow deviate from the teacher (Stanton et al., 2021). But what is the nature of these deviations, and how do they relate to gains in generalization? We investigate these questions through a series of experiments across image and language classification datasets. First, we observe that distillation consistently deviates in a characteristic way: on points where the teacher has low confidence, the student achieves even lower confidence than the teacher. Secondly, we find that deviations in the initial dynamics of training are not crucial -- simply switching to distillation loss in the middle of training can recover much of its gains. We then provide two parallel theoretical perspectives to understand the role of student-teacher deviations in our experiments, one casting distillation as a regularizer in eigenspace, and another as a gradient denoiser. Our analysis bridges several gaps between existing theory and practice by (a) focusing on gradient-descent training, (b) by avoiding label noise assumptions, and (c) by unifying several disjoint empirical and theoretical findings.