Chong You
Spark Transformer: Reactivating Sparsity in FFN and Attention
Jun 07, 2025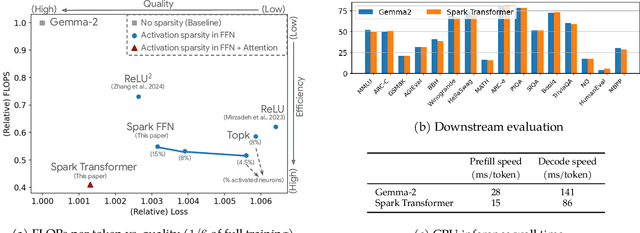
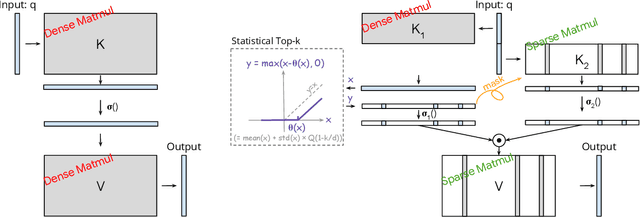
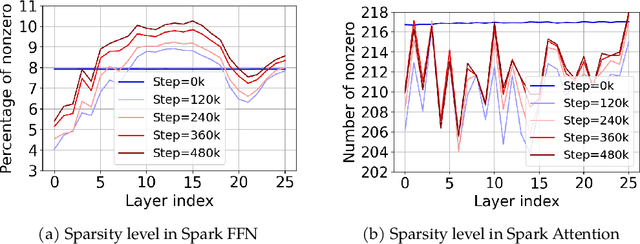
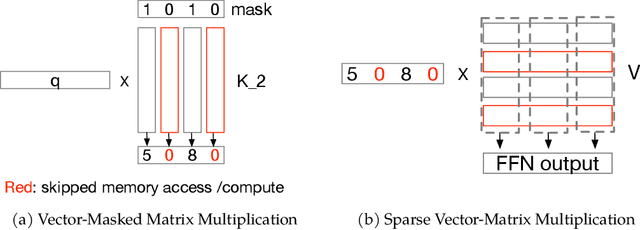
Abstract:The discovery of the lazy neuron phenomenon in trained Transformers, where the vast majority of neurons in their feed-forward networks (FFN) are inactive for each token, has spurred tremendous interests in activation sparsity for enhancing large model efficiency. While notable progress has been made in translating such sparsity to wall-time benefits, modern Transformers have moved away from the ReLU activation function crucial to this phenomenon. Existing efforts on re-introducing activation sparsity often degrade model quality, increase parameter count, complicate or slow down training. Sparse attention, the application of sparse activation to the attention mechanism, often faces similar challenges. This paper introduces the Spark Transformer, a novel architecture that achieves a high level of activation sparsity in both FFN and the attention mechanism while maintaining model quality, parameter count, and standard training procedures. Our method realizes sparsity via top-k masking for explicit control over sparsity level. Crucially, we introduce statistical top-k, a hardware-accelerator-friendly, linear-time approximate algorithm that avoids costly sorting and mitigates significant training slowdown from standard top-$k$ operators. Furthermore, Spark Transformer reallocates existing FFN parameters and attention key embeddings to form a low-cost predictor for identifying activated entries. This design not only mitigates quality loss from enforced sparsity, but also enhances wall-time benefit. Pretrained with the Gemma-2 recipe, Spark Transformer demonstrates competitive performance on standard benchmarks while exhibiting significant sparsity: only 8% of FFN neurons are activated, and each token attends to a maximum of 256 tokens. This sparsity translates to a 2.5x reduction in FLOPs, leading to decoding wall-time speedups of up to 1.79x on CPU and 1.40x on GPU.
Efficient and Asymptotically Unbiased Constrained Decoding for Large Language Models
Apr 12, 2025Abstract:In real-world applications of large language models, outputs are often required to be confined: selecting items from predefined product or document sets, generating phrases that comply with safety standards, or conforming to specialized formatting styles. To control the generation, constrained decoding has been widely adopted. However, existing prefix-tree-based constrained decoding is inefficient under GPU-based model inference paradigms, and it introduces unintended biases into the output distribution. This paper introduces Dynamic Importance Sampling for Constrained Decoding (DISC) with GPU-based Parallel Prefix-Verification (PPV), a novel algorithm that leverages dynamic importance sampling to achieve theoretically guaranteed asymptotic unbiasedness and overcomes the inefficiency of prefix-tree. Extensive experiments demonstrate the superiority of our method over existing methods in both efficiency and output quality. These results highlight the potential of our methods to improve constrained generation in applications where adherence to specific constraints is essential.
HiRE: High Recall Approximate Top-$k$ Estimation for Efficient LLM Inference
Feb 14, 2024



Abstract:Autoregressive decoding with generative Large Language Models (LLMs) on accelerators (GPUs/TPUs) is often memory-bound where most of the time is spent on transferring model parameters from high bandwidth memory (HBM) to cache. On the other hand, recent works show that LLMs can maintain quality with significant sparsity/redundancy in the feedforward (FFN) layers by appropriately training the model to operate on a top-$k$ fraction of rows/columns (where $k \approx 0.05$), there by suggesting a way to reduce the transfer of model parameters, and hence latency. However, exploiting this sparsity for improving latency is hindered by the fact that identifying top rows/columns is data-dependent and is usually performed using full matrix operations, severely limiting potential gains. To address these issues, we introduce HiRE (High Recall Approximate Top-k Estimation). HiRE comprises of two novel components: (i) a compression scheme to cheaply predict top-$k$ rows/columns with high recall, followed by full computation restricted to the predicted subset, and (ii) DA-TOP-$k$: an efficient multi-device approximate top-$k$ operator. We demonstrate that on a one billion parameter model, HiRE applied to both the softmax as well as feedforward layers, achieves almost matching pretraining and downstream accuracy, and speeds up inference latency by $1.47\times$ on a single TPUv5e device.
Generalized Neural Collapse for a Large Number of Classes
Oct 15, 2023



Abstract:Neural collapse provides an elegant mathematical characterization of learned last layer representations (a.k.a. features) and classifier weights in deep classification models. Such results not only provide insights but also motivate new techniques for improving practical deep models. However, most of the existing empirical and theoretical studies in neural collapse focus on the case that the number of classes is small relative to the dimension of the feature space. This paper extends neural collapse to cases where the number of classes are much larger than the dimension of feature space, which broadly occur for language models, retrieval systems, and face recognition applications. We show that the features and classifier exhibit a generalized neural collapse phenomenon, where the minimum one-vs-rest margins is maximized.We provide empirical study to verify the occurrence of generalized neural collapse in practical deep neural networks. Moreover, we provide theoretical study to show that the generalized neural collapse provably occurs under unconstrained feature model with spherical constraint, under certain technical conditions on feature dimension and number of classes.
It's an Alignment, Not a Trade-off: Revisiting Bias and Variance in Deep Models
Oct 13, 2023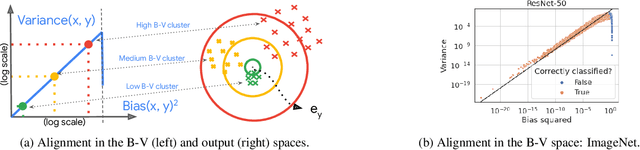

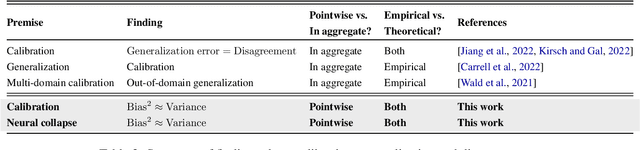
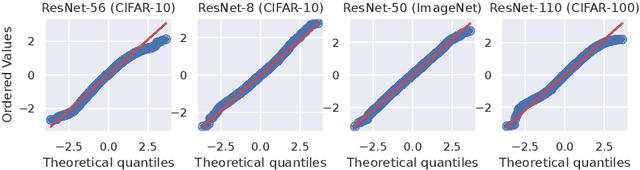
Abstract:Classical wisdom in machine learning holds that the generalization error can be decomposed into bias and variance, and these two terms exhibit a \emph{trade-off}. However, in this paper, we show that for an ensemble of deep learning based classification models, bias and variance are \emph{aligned} at a sample level, where squared bias is approximately \emph{equal} to variance for correctly classified sample points. We present empirical evidence confirming this phenomenon in a variety of deep learning models and datasets. Moreover, we study this phenomenon from two theoretical perspectives: calibration and neural collapse. We first show theoretically that under the assumption that the models are well calibrated, we can observe the bias-variance alignment. Second, starting from the picture provided by the neural collapse theory, we show an approximate correlation between bias and variance.
Functional Interpolation for Relative Positions Improves Long Context Transformers
Oct 06, 2023Abstract:Preventing the performance decay of Transformers on inputs longer than those used for training has been an important challenge in extending the context length of these models. Though the Transformer architecture has fundamentally no limits on the input sequence lengths it can process, the choice of position encoding used during training can limit the performance of these models on longer inputs. We propose a novel functional relative position encoding with progressive interpolation, FIRE, to improve Transformer generalization to longer contexts. We theoretically prove that this can represent some of the popular relative position encodings, such as T5's RPE, Alibi, and Kerple. We next empirically show that FIRE models have better generalization to longer contexts on both zero-shot language modeling and long text benchmarks.
Revisiting Sparse Convolutional Model for Visual Recognition
Oct 24, 2022



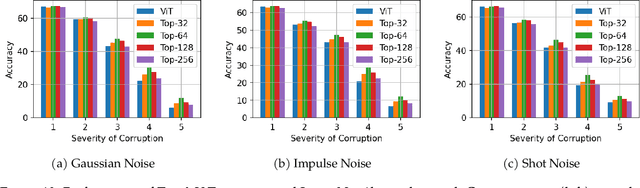
Abstract:Despite strong empirical performance for image classification, deep neural networks are often regarded as ``black boxes'' and they are difficult to interpret. On the other hand, sparse convolutional models, which assume that a signal can be expressed by a linear combination of a few elements from a convolutional dictionary, are powerful tools for analyzing natural images with good theoretical interpretability and biological plausibility. However, such principled models have not demonstrated competitive performance when compared with empirically designed deep networks. This paper revisits the sparse convolutional modeling for image classification and bridges the gap between good empirical performance (of deep learning) and good interpretability (of sparse convolutional models). Our method uses differentiable optimization layers that are defined from convolutional sparse coding as drop-in replacements of standard convolutional layers in conventional deep neural networks. We show that such models have equally strong empirical performance on CIFAR-10, CIFAR-100, and ImageNet datasets when compared to conventional neural networks. By leveraging stable recovery property of sparse modeling, we further show that such models can be much more robust to input corruptions as well as adversarial perturbations in testing through a simple proper trade-off between sparse regularization and data reconstruction terms. Source code can be found at https://github.com/Delay-Xili/SDNet.
Large Models are Parsimonious Learners: Activation Sparsity in Trained Transformers
Oct 12, 2022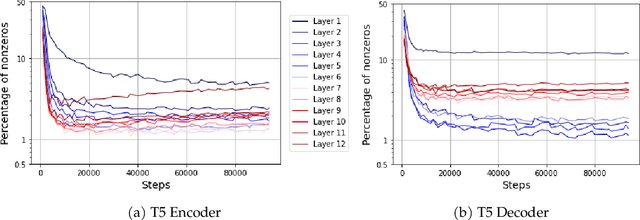

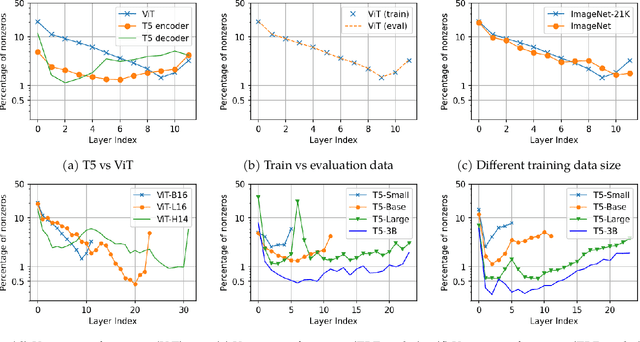
Abstract:This paper studies the curious phenomenon for machine learning models with Transformer architectures that their activation maps are sparse. By activation map we refer to the intermediate output of the multi-layer perceptrons (MLPs) after a ReLU activation function, and by "sparse" we mean that on average very few entries (e.g., 3.0% for T5-Base and 6.3% for ViT-B16) are nonzero for each input to MLP. Moreover, larger Transformers with more layers and wider MLP hidden dimensions are sparser as measured by the percentage of nonzero entries. Through extensive experiments we demonstrate that the emergence of sparsity is a prevalent phenomenon that occurs for both natural language processing and vision tasks, on both training and evaluation data, for Transformers of various configurations, at layers of all depth levels, as well as for other architectures including MLP-mixers and 2-layer MLPs. We show that sparsity also emerges using training datasets with random labels, or with random inputs, or with infinite amount of data, demonstrating that sparsity is not a result of a specific family of datasets. We discuss how sparsity immediately implies a way to significantly reduce the FLOP count and improve efficiency for Transformers. Moreover, we demonstrate perhaps surprisingly that enforcing an even sparser activation via Top-k thresholding with a small value of k brings a collection of desired but missing properties for Transformers, namely less sensitivity to noisy training data, more robustness to input corruptions, and better calibration for their prediction confidence.
Are All Losses Created Equal: A Neural Collapse Perspective
Oct 08, 2022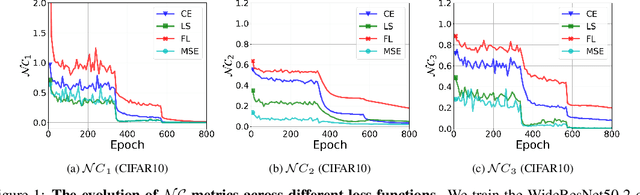
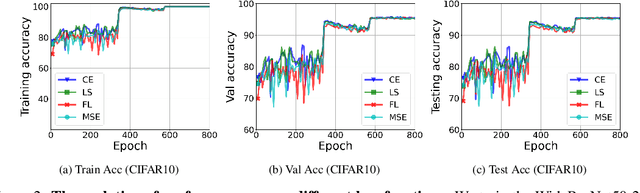
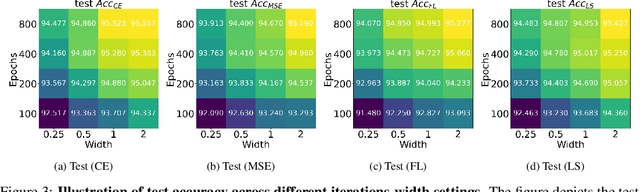
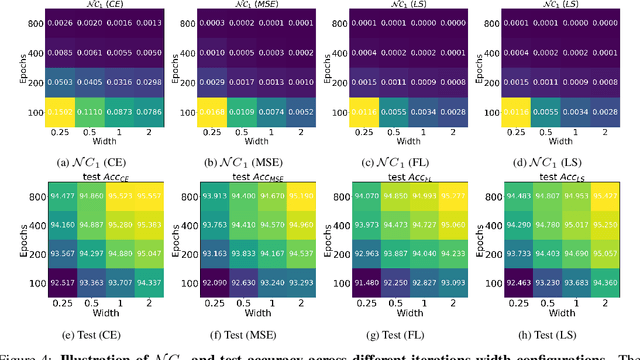
Abstract:While cross entropy (CE) is the most commonly used loss to train deep neural networks for classification tasks, many alternative losses have been developed to obtain better empirical performance. Among them, which one is the best to use is still a mystery, because there seem to be multiple factors affecting the answer, such as properties of the dataset, the choice of network architecture, and so on. This paper studies the choice of loss function by examining the last-layer features of deep networks, drawing inspiration from a recent line work showing that the global optimal solution of CE and mean-square-error (MSE) losses exhibits a Neural Collapse phenomenon. That is, for sufficiently large networks trained until convergence, (i) all features of the same class collapse to the corresponding class mean and (ii) the means associated with different classes are in a configuration where their pairwise distances are all equal and maximized. We extend such results and show through global solution and landscape analyses that a broad family of loss functions including commonly used label smoothing (LS) and focal loss (FL) exhibits Neural Collapse. Hence, all relevant losses(i.e., CE, LS, FL, MSE) produce equivalent features on training data. Based on the unconstrained feature model assumption, we provide either the global landscape analysis for LS loss or the local landscape analysis for FL loss and show that the (only!) global minimizers are neural collapse solutions, while all other critical points are strict saddles whose Hessian exhibit negative curvature directions either in the global scope for LS loss or in the local scope for FL loss near the optimal solution. The experiments further show that Neural Collapse features obtained from all relevant losses lead to largely identical performance on test data as well, provided that the network is sufficiently large and trained until convergence.
Teacher Guided Training: An Efficient Framework for Knowledge Transfer
Aug 14, 2022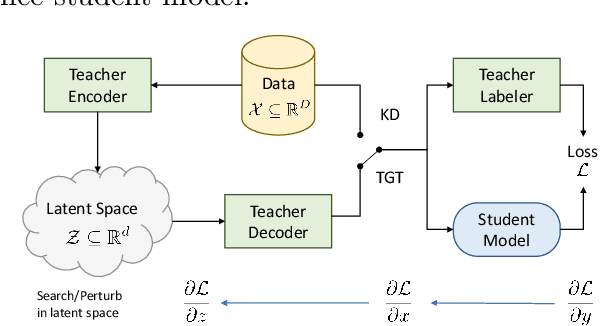
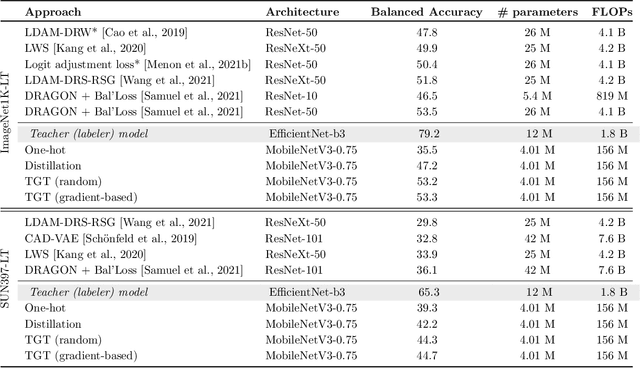
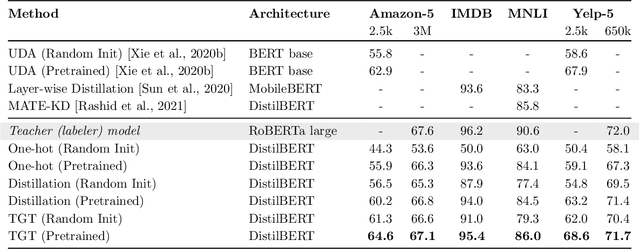
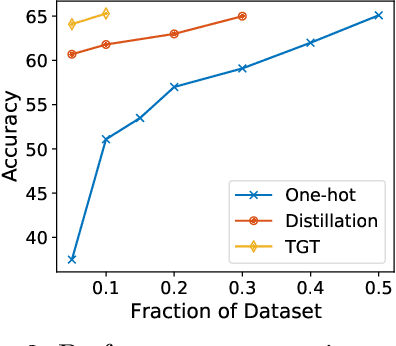
Abstract:The remarkable performance gains realized by large pretrained models, e.g., GPT-3, hinge on the massive amounts of data they are exposed to during training. Analogously, distilling such large models to compact models for efficient deployment also necessitates a large amount of (labeled or unlabeled) training data. In this paper, we propose the teacher-guided training (TGT) framework for training a high-quality compact model that leverages the knowledge acquired by pretrained generative models, while obviating the need to go through a large volume of data. TGT exploits the fact that the teacher has acquired a good representation of the underlying data domain, which typically corresponds to a much lower dimensional manifold than the input space. Furthermore, we can use the teacher to explore input space more efficiently through sampling or gradient-based methods; thus, making TGT especially attractive for limited data or long-tail settings. We formally capture this benefit of proposed data-domain exploration in our generalization bounds. We find that TGT can improve accuracy on several image classification benchmarks as well as a range of text classification and retrieval tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge