Large Models are Parsimonious Learners: Activation Sparsity in Trained Transformers

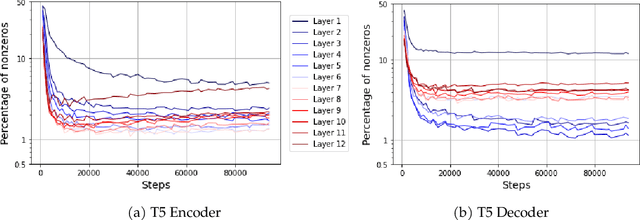
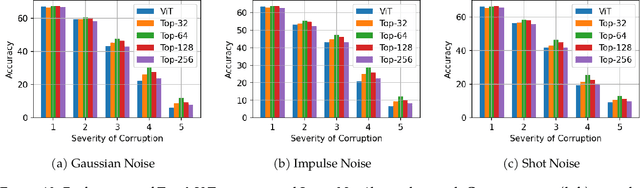
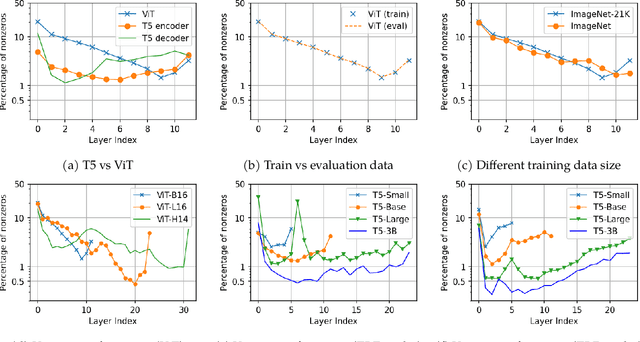
This paper studies the curious phenomenon for machine learning models with Transformer architectures that their activation maps are sparse. By activation map we refer to the intermediate output of the multi-layer perceptrons (MLPs) after a ReLU activation function, and by "sparse" we mean that on average very few entries (e.g., 3.0% for T5-Base and 6.3% for ViT-B16) are nonzero for each input to MLP. Moreover, larger Transformers with more layers and wider MLP hidden dimensions are sparser as measured by the percentage of nonzero entries. Through extensive experiments we demonstrate that the emergence of sparsity is a prevalent phenomenon that occurs for both natural language processing and vision tasks, on both training and evaluation data, for Transformers of various configurations, at layers of all depth levels, as well as for other architectures including MLP-mixers and 2-layer MLPs. We show that sparsity also emerges using training datasets with random labels, or with random inputs, or with infinite amount of data, demonstrating that sparsity is not a result of a specific family of datasets. We discuss how sparsity immediately implies a way to significantly reduce the FLOP count and improve efficiency for Transformers. Moreover, we demonstrate perhaps surprisingly that enforcing an even sparser activation via Top-k thresholding with a small value of k brings a collection of desired but missing properties for Transformers, namely less sensitivity to noisy training data, more robustness to input corruptions, and better calibration for their prediction confidence.

TPU-KNN: K Nearest Neighbor Search at Peak FLOP/s

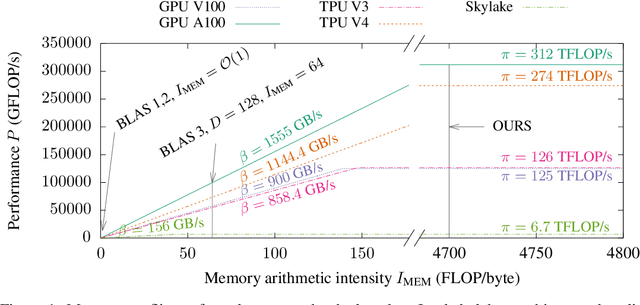
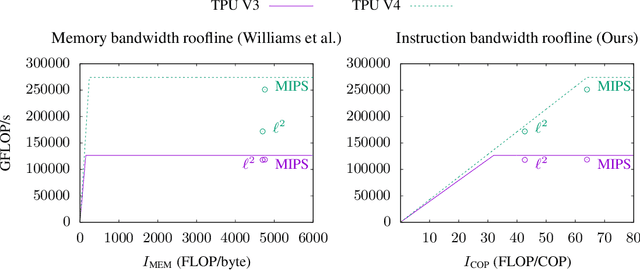
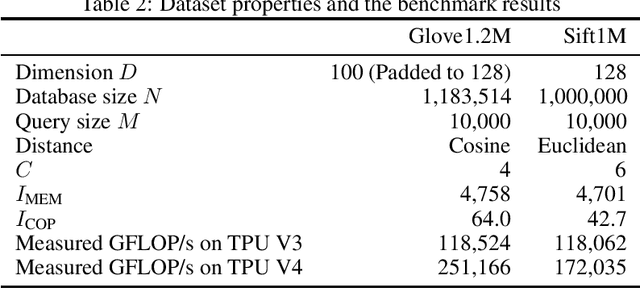
This paper presents a novel nearest neighbor search algorithm achieving TPU (Google Tensor Processing Unit) peak performance, outperforming state-of-the-art GPU algorithms with similar level of recall. The design of the proposed algorithm is motivated by an accurate accelerator performance model that takes into account both the memory and instruction bottlenecks. Our algorithm comes with an analytical guarantee of recall in expectation and does not require maintaining sophisticated index data structure or tuning, making it suitable for applications with frequent updates. Our work is available in the open-source package of Jax and Tensorflow on TPU.

New Loss Functions for Fast Maximum Inner Product Search

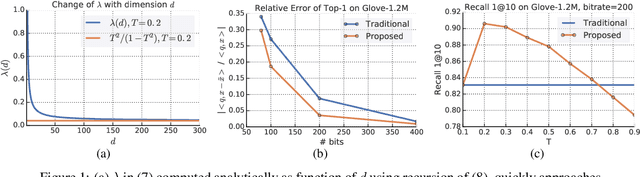
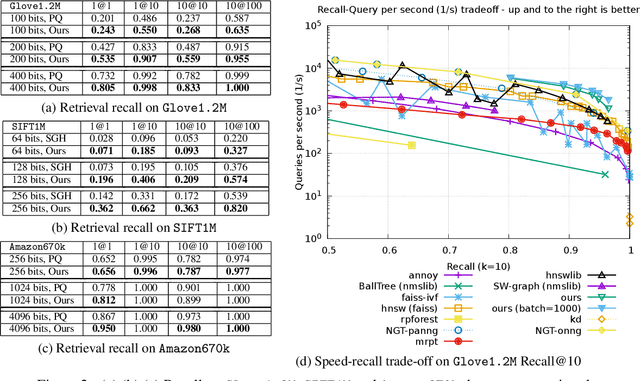
Quantization based methods are popular for solving large scale maximum inner product search problems. However, in most traditional quantization works, the objective is to minimize the reconstruction error for datapoints to be searched. In this work, we focus directly on minimizing error in inner product approximation and derive a new class of quantization loss functions. One key aspect of the new loss functions is that we weight the error term based on the value of the inner product, giving more importance to pairs of queries and datapoints whose inner products are high. We provide theoretical grounding to the new quantization loss function, which is simple, intuitive and able to work with a variety of quantization techniques, including binary quantization and product quantization. We conduct experiments on standard benchmarking datasets to demonstrate that our method using the new objective outperforms other state-of-the-art methods.