New Loss Functions for Fast Maximum Inner Product Search

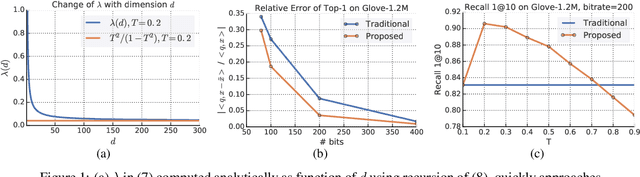
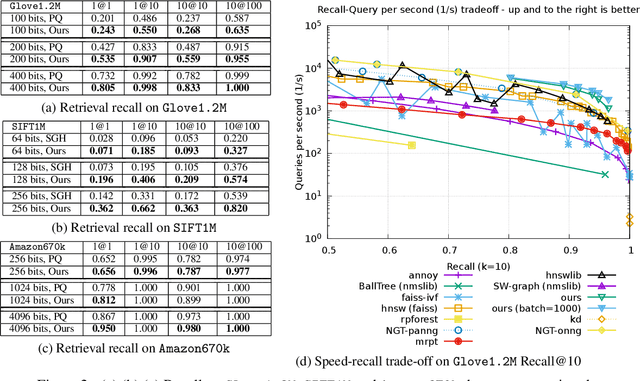
Quantization based methods are popular for solving large scale maximum inner product search problems. However, in most traditional quantization works, the objective is to minimize the reconstruction error for datapoints to be searched. In this work, we focus directly on minimizing error in inner product approximation and derive a new class of quantization loss functions. One key aspect of the new loss functions is that we weight the error term based on the value of the inner product, giving more importance to pairs of queries and datapoints whose inner products are high. We provide theoretical grounding to the new quantization loss function, which is simple, intuitive and able to work with a variety of quantization techniques, including binary quantization and product quantization. We conduct experiments on standard benchmarking datasets to demonstrate that our method using the new objective outperforms other state-of-the-art methods.

Truncated Laplacian Mechanism for Approximate Differential Privacy

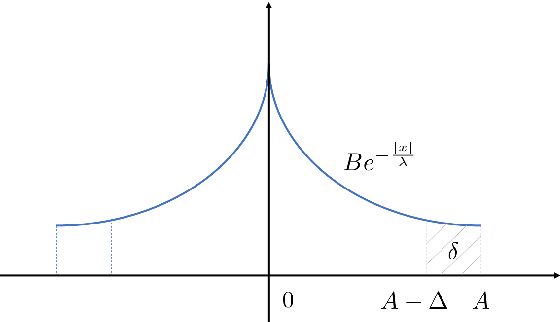
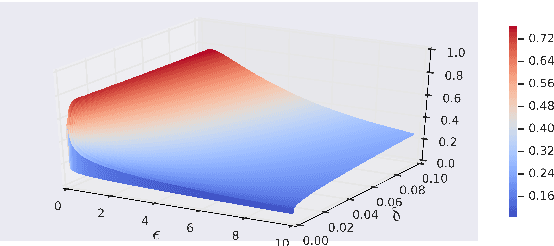
We derive a class of noise probability distributions to preserve $(\epsilon, \delta)$-differential privacy for single real-valued query function. The proposed noise distribution has a truncated exponential probability density function, which can be viewed as a truncated Laplacian distribution. We show the near-optimality of the proposed \emph{truncated Laplacian} mechanism in various privacy regimes in the context of minimizing the noise amplitude and noise power. Numeric experiments show the improvement of the truncated Laplacian mechanism over the optimal Gaussian mechanism by significantly reducing the noise amplitude and noise power in various privacy regions.

Optimal Noise-Adding Mechanism in Additive Differential Privacy

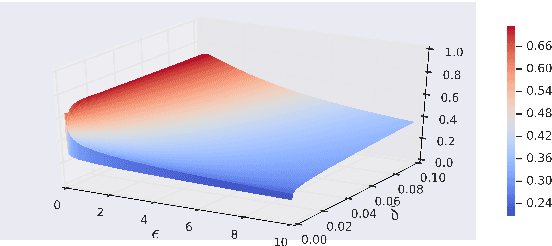
We derive the optimal $(0, \delta)$-differentially private query-output independent noise-adding mechanism for single real-valued query function under a general cost-minimization framework. Under a mild technical condition, we show that the optimal noise probability distribution is a uniform distribution with a probability mass at the origin. We explicitly derive the optimal noise distribution for general $\ell^n$ cost functions, including $\ell^1$ (for noise magnitude) and $\ell^2$ (for noise power) cost functions, and show that the probability concentration on the origin occurs when $\delta > \frac{n}{n+1}$. Our result demonstrates an improvement over the existing Gaussian mechanisms by a factor of two and three for $(0,\delta)$-differential privacy in the high privacy regime in the context of minimizing the noise magnitude and noise power, and the gain is more pronounced in the low privacy regime. Our result is consistent with the existing result for $(0,\delta)$-differential privacy in the discrete setting, and identifies a probability concentration phenomenon in the continuous setting.

On the Local Correctness of L^1 Minimization for Dictionary Learning

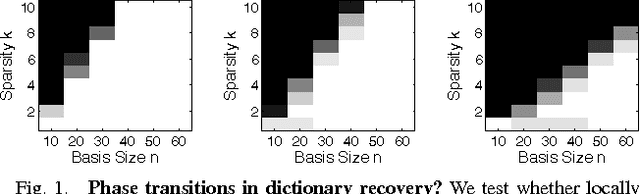
The idea that many important classes of signals can be well-represented by linear combinations of a small set of atoms selected from a given dictionary has had dramatic impact on the theory and practice of signal processing. For practical problems in which an appropriate sparsifying dictionary is not known ahead of time, a very popular and successful heuristic is to search for a dictionary that minimizes an appropriate sparsity surrogate over a given set of sample data. While this idea is appealing, the behavior of these algorithms is largely a mystery; although there is a body of empirical evidence suggesting they do learn very effective representations, there is little theory to guarantee when they will behave correctly, or when the learned dictionary can be expected to generalize. In this paper, we take a step towards such a theory. We show that under mild hypotheses, the dictionary learning problem is locally well-posed: the desired solution is indeed a local minimum of the $\ell^1$ norm. Namely, if $\mb A \in \Re^{m \times n}$ is an incoherent (and possibly overcomplete) dictionary, and the coefficients $\mb X \in \Re^{n \times p}$ follow a random sparse model, then with high probability $(\mb A,\mb X)$ is a local minimum of the $\ell^1$ norm over the manifold of factorizations $(\mb A',\mb X')$ satisfying $\mb A' \mb X' = \mb Y$, provided the number of samples $p = \Omega(n^3 k)$. For overcomplete $\mb A$, this is the first result showing that the dictionary learning problem is locally solvable. Our analysis draws on tools developed for the problem of completing a low-rank matrix from a small subset of its entries, which allow us to overcome a number of technical obstacles; in particular, the absence of the restricted isometry property.