Truncated Laplacian Mechanism for Approximate Differential Privacy

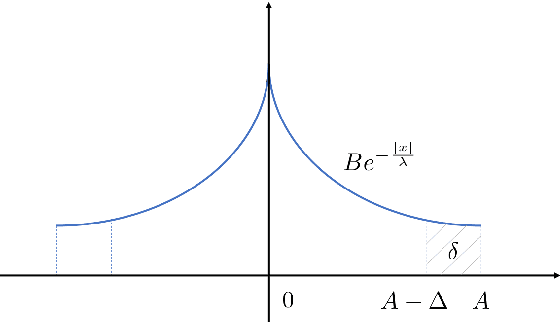
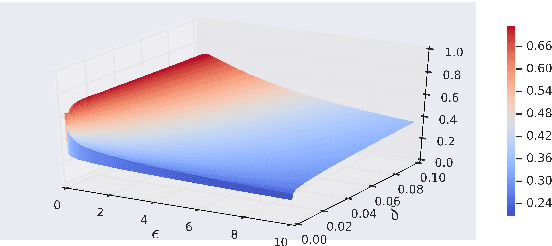
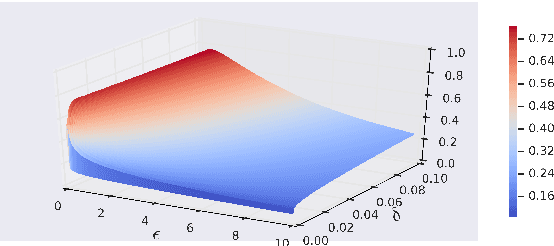
We derive a class of noise probability distributions to preserve $(\epsilon, \delta)$-differential privacy for single real-valued query function. The proposed noise distribution has a truncated exponential probability density function, which can be viewed as a truncated Laplacian distribution. We show the near-optimality of the proposed \emph{truncated Laplacian} mechanism in various privacy regimes in the context of minimizing the noise amplitude and noise power. Numeric experiments show the improvement of the truncated Laplacian mechanism over the optimal Gaussian mechanism by significantly reducing the noise amplitude and noise power in various privacy regions.