SOAR: Improved Indexing for Approximate Nearest Neighbor Search

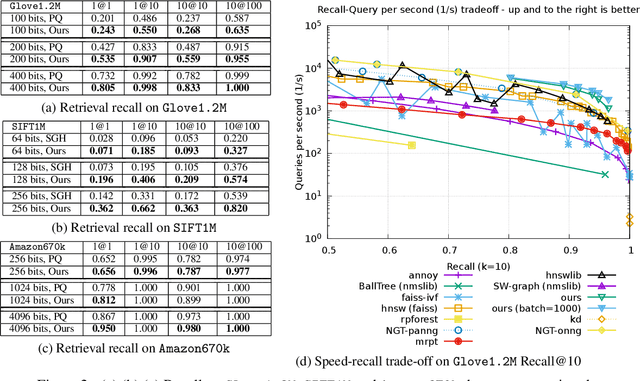
This paper introduces SOAR: Spilling with Orthogonality-Amplified Residuals, a novel data indexing technique for approximate nearest neighbor (ANN) search. SOAR extends upon previous approaches to ANN search, such as spill trees, that utilize multiple redundant representations while partitioning the data to reduce the probability of missing a nearest neighbor during search. Rather than training and computing these redundant representations independently, however, SOAR uses an orthogonality-amplified residual loss, which optimizes each representation to compensate for cases where other representations perform poorly. This drastically improves the overall index quality, resulting in state-of-the-art ANN benchmark performance while maintaining fast indexing times and low memory consumption.

ReST meets ReAct: Self-Improvement for Multi-Step Reasoning LLM Agent

Answering complex natural language questions often necessitates multi-step reasoning and integrating external information. Several systems have combined knowledge retrieval with a large language model (LLM) to answer such questions. These systems, however, suffer from various failure cases, and we cannot directly train them end-to-end to fix such failures, as interaction with external knowledge is non-differentiable. To address these deficiencies, we define a ReAct-style LLM agent with the ability to reason and act upon external knowledge. We further refine the agent through a ReST-like method that iteratively trains on previous trajectories, employing growing-batch reinforcement learning with AI feedback for continuous self-improvement and self-distillation. Starting from a prompted large model and after just two iterations of the algorithm, we can produce a fine-tuned small model that achieves comparable performance on challenging compositional question-answering benchmarks with two orders of magnitude fewer parameters.

Automating Nearest Neighbor Search Configuration with Constrained Optimization

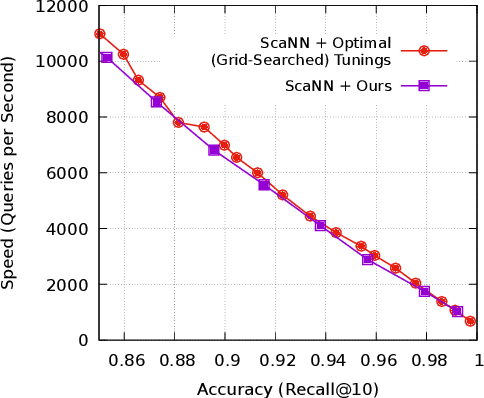
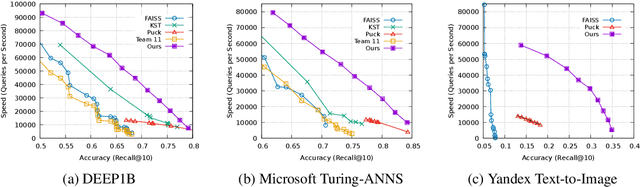
The approximate nearest neighbor (ANN) search problem is fundamental to efficiently serving many real-world machine learning applications. A number of techniques have been developed for ANN search that are efficient, accurate, and scalable. However, such techniques typically have a number of parameters that affect the speed-recall tradeoff, and exhibit poor performance when such parameters aren't properly set. Tuning these parameters has traditionally been a manual process, demanding in-depth knowledge of the underlying search algorithm. This is becoming an increasingly unrealistic demand as ANN search grows in popularity. To tackle this obstacle to ANN adoption, this work proposes a constrained optimization-based approach to tuning quantization-based ANN algorithms. Our technique takes just a desired search cost or recall as input, and then generates tunings that, empirically, are very close to the speed-recall Pareto frontier and give leading performance on standard benchmarks.

Large Models are Parsimonious Learners: Activation Sparsity in Trained Transformers

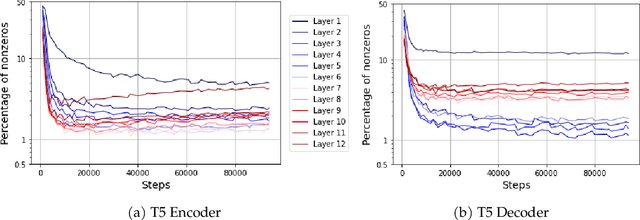
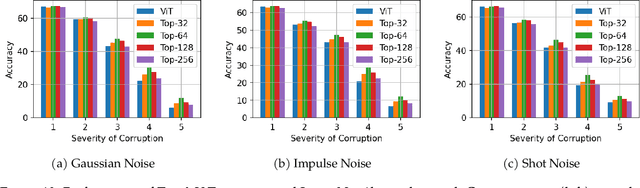
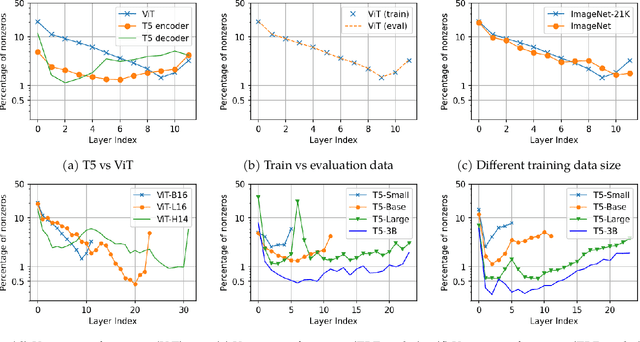
This paper studies the curious phenomenon for machine learning models with Transformer architectures that their activation maps are sparse. By activation map we refer to the intermediate output of the multi-layer perceptrons (MLPs) after a ReLU activation function, and by "sparse" we mean that on average very few entries (e.g., 3.0% for T5-Base and 6.3% for ViT-B16) are nonzero for each input to MLP. Moreover, larger Transformers with more layers and wider MLP hidden dimensions are sparser as measured by the percentage of nonzero entries. Through extensive experiments we demonstrate that the emergence of sparsity is a prevalent phenomenon that occurs for both natural language processing and vision tasks, on both training and evaluation data, for Transformers of various configurations, at layers of all depth levels, as well as for other architectures including MLP-mixers and 2-layer MLPs. We show that sparsity also emerges using training datasets with random labels, or with random inputs, or with infinite amount of data, demonstrating that sparsity is not a result of a specific family of datasets. We discuss how sparsity immediately implies a way to significantly reduce the FLOP count and improve efficiency for Transformers. Moreover, we demonstrate perhaps surprisingly that enforcing an even sparser activation via Top-k thresholding with a small value of k brings a collection of desired but missing properties for Transformers, namely less sensitivity to noisy training data, more robustness to input corruptions, and better calibration for their prediction confidence.

Decoupled Context Processing for Context Augmented Language Modeling

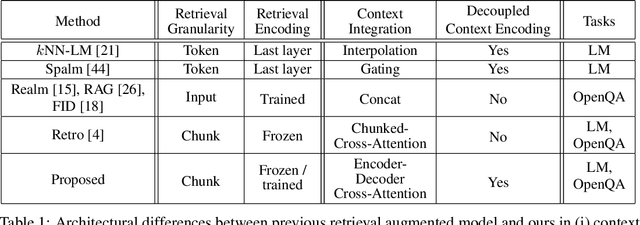
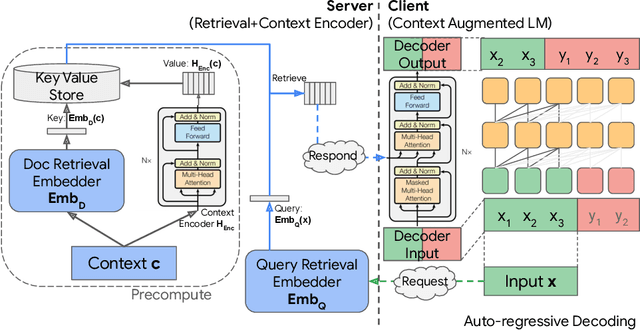
Language models can be augmented with a context retriever to incorporate knowledge from large external databases. By leveraging retrieved context, the neural network does not have to memorize the massive amount of world knowledge within its internal parameters, leading to better parameter efficiency, interpretability and modularity. In this paper we examined a simple yet effective architecture for incorporating external context into language models based on decoupled Encoder Decoder architecture. We showed that such a simple architecture achieves competitive results on auto-regressive language modeling and open domain question answering tasks. We also analyzed the behavior of the proposed model which performs grounded context transfer. Finally we discussed the computational implications of such retrieval augmented models.

TPU-KNN: K Nearest Neighbor Search at Peak FLOP/s

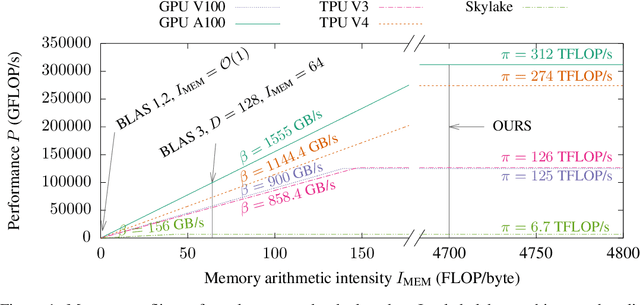
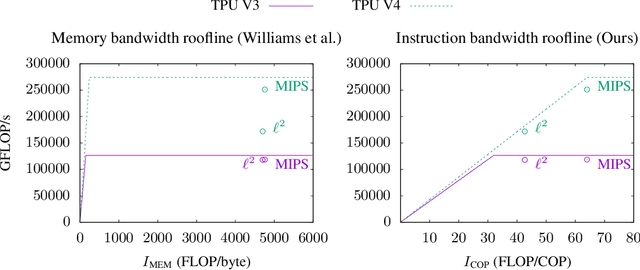
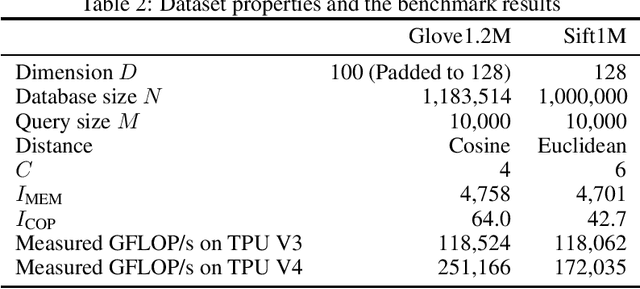
This paper presents a novel nearest neighbor search algorithm achieving TPU (Google Tensor Processing Unit) peak performance, outperforming state-of-the-art GPU algorithms with similar level of recall. The design of the proposed algorithm is motivated by an accurate accelerator performance model that takes into account both the memory and instruction bottlenecks. Our algorithm comes with an analytical guarantee of recall in expectation and does not require maintaining sophisticated index data structure or tuning, making it suitable for applications with frequent updates. Our work is available in the open-source package of Jax and Tensorflow on TPU.

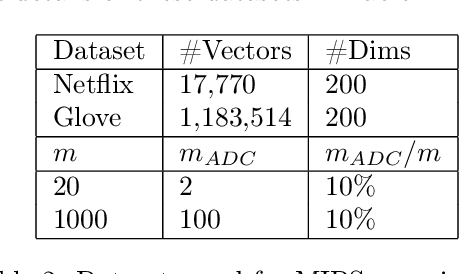
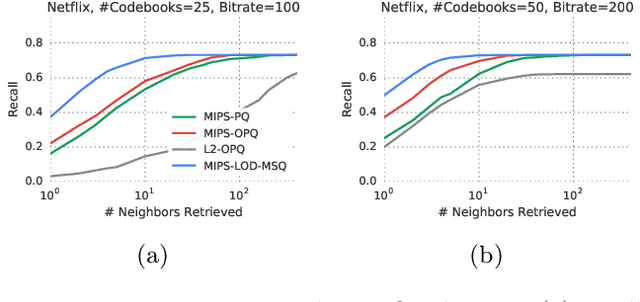
New Loss Functions for Fast Maximum Inner Product Search

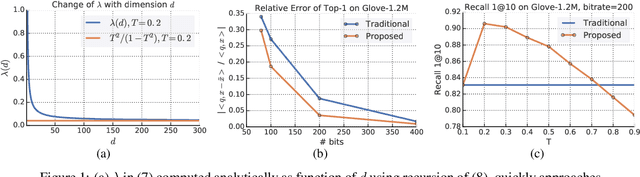
Quantization based methods are popular for solving large scale maximum inner product search problems. However, in most traditional quantization works, the objective is to minimize the reconstruction error for datapoints to be searched. In this work, we focus directly on minimizing error in inner product approximation and derive a new class of quantization loss functions. One key aspect of the new loss functions is that we weight the error term based on the value of the inner product, giving more importance to pairs of queries and datapoints whose inner products are high. We provide theoretical grounding to the new quantization loss function, which is simple, intuitive and able to work with a variety of quantization techniques, including binary quantization and product quantization. We conduct experiments on standard benchmarking datasets to demonstrate that our method using the new objective outperforms other state-of-the-art methods.

Local Orthogonal Decomposition for Maximum Inner Product Search

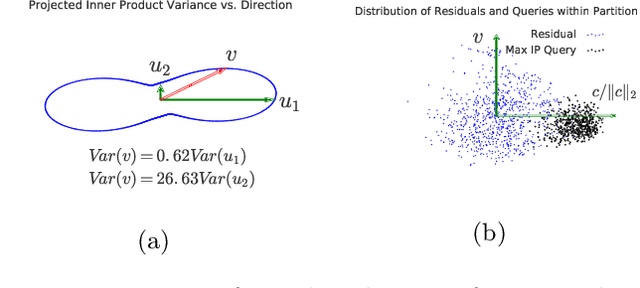
Inverted file and asymmetric distance computation (IVFADC) have been successfully applied to approximate nearest neighbor search and subsequently maximum inner product search. In such a framework, vector quantization is used for coarse partitioning while product quantization is used for quantizing residuals. In the original IVFADC as well as all of its variants, after residuals are computed, the second production quantization step is completely independent of the first vector quantization step. In this work, we seek to exploit the connection between these two steps when we perform non-exhaustive search. More specifically, we decompose a residual vector locally into two orthogonal components and perform uniform quantization and multiscale quantization to each component respectively. The proposed method, called local orthogonal decomposition, combined with multiscale quantization consistently achieves higher recall than previous methods under the same bitrates. We conduct comprehensive experiments on large scale datasets as well as detailed ablation tests, demonstrating effectiveness of our method.

Efficient Inner Product Approximation in Hybrid Spaces

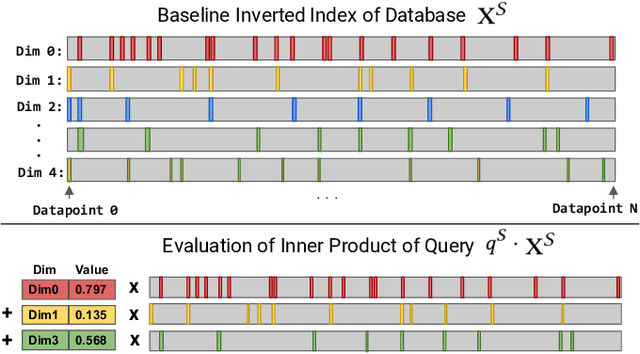
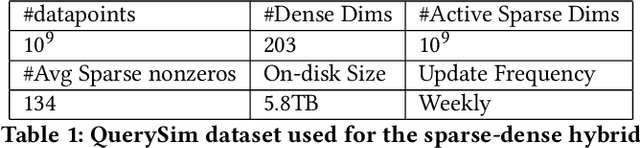
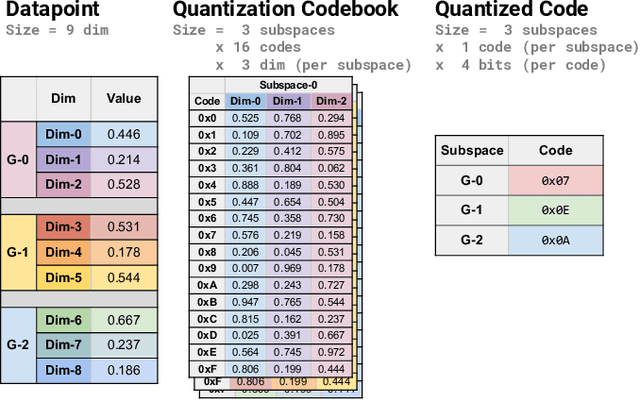
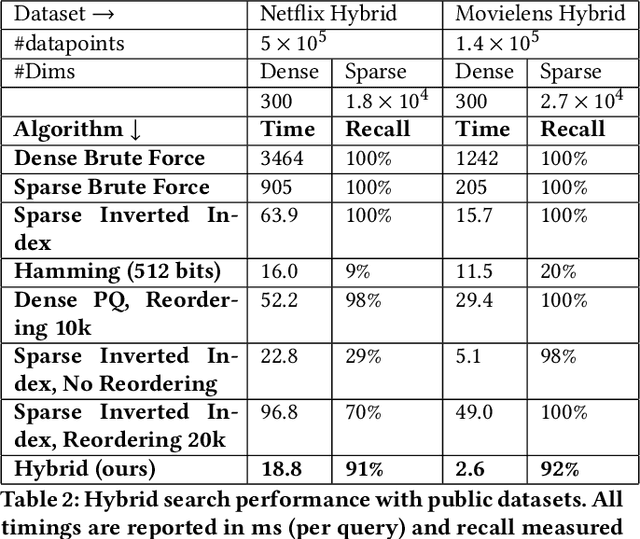
Many emerging use cases of data mining and machine learning operate on large datasets with data from heterogeneous sources, specifically with both sparse and dense components. For example, dense deep neural network embedding vectors are often used in conjunction with sparse textual features to provide high dimensional hybrid representation of documents. Efficient search in such hybrid spaces is very challenging as the techniques that perform well for sparse vectors have little overlap with those that work well for dense vectors. Popular techniques like Locality Sensitive Hashing (LSH) and its data-dependent variants also do not give good accuracy in high dimensional hybrid spaces. Even though hybrid scenarios are becoming more prevalent, currently there exist no efficient techniques in literature that are both fast and accurate. In this paper, we propose a technique that approximates the inner product computation in hybrid vectors, leading to substantial speedup in search while maintaining high accuracy. We also propose efficient data structures that exploit modern computer architectures, resulting in orders of magnitude faster search than the existing baselines. The performance of the proposed method is demonstrated on several datasets including a very large scale industrial dataset containing one billion vectors in a billion dimensional space, achieving over 10x speedup and higher accuracy against competitive baselines.

Truncated Laplacian Mechanism for Approximate Differential Privacy

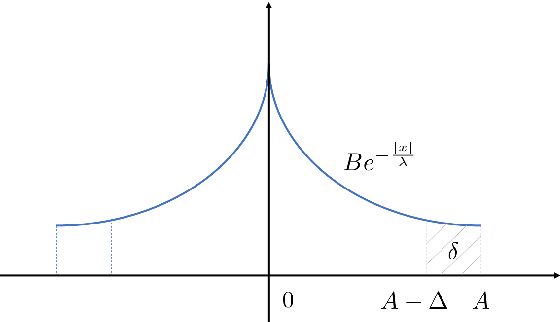
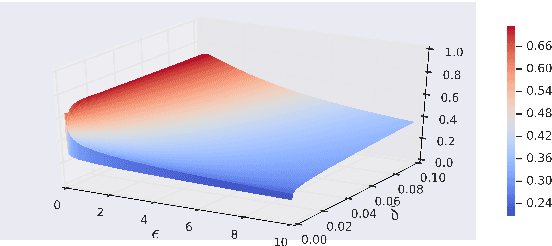
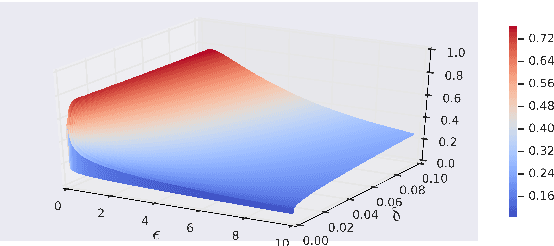
We derive a class of noise probability distributions to preserve $(\epsilon, \delta)$-differential privacy for single real-valued query function. The proposed noise distribution has a truncated exponential probability density function, which can be viewed as a truncated Laplacian distribution. We show the near-optimality of the proposed \emph{truncated Laplacian} mechanism in various privacy regimes in the context of minimizing the noise amplitude and noise power. Numeric experiments show the improvement of the truncated Laplacian mechanism over the optimal Gaussian mechanism by significantly reducing the noise amplitude and noise power in various privacy regions.