On the Role of Depth and Looping for In-Context Learning with Task Diversity

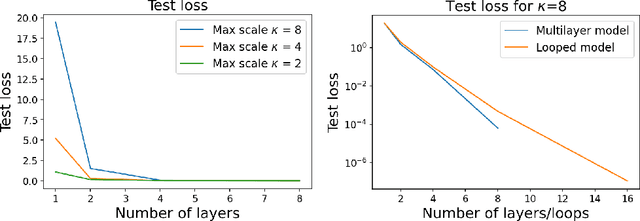
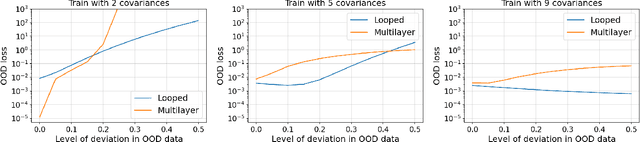
The intriguing in-context learning (ICL) abilities of deep Transformer models have lately garnered significant attention. By studying in-context linear regression on unimodal Gaussian data, recent empirical and theoretical works have argued that ICL emerges from Transformers' abilities to simulate learning algorithms like gradient descent. However, these works fail to capture the remarkable ability of Transformers to learn multiple tasks in context. To this end, we study in-context learning for linear regression with diverse tasks, characterized by data covariance matrices with condition numbers ranging from $[1, \kappa]$, and highlight the importance of depth in this setting. More specifically, (a) we show theoretical lower bounds of $\log(\kappa)$ (or $\sqrt{\kappa}$) linear attention layers in the unrestricted (or restricted) attention setting and, (b) we show that multilayer Transformers can indeed solve such tasks with a number of layers that matches the lower bounds. However, we show that this expressivity of multilayer Transformer comes at the price of robustness. In particular, multilayer Transformers are not robust to even distributional shifts as small as $O(e^{-L})$ in Wasserstein distance, where $L$ is the depth of the network. We then demonstrate that Looped Transformers -- a special class of multilayer Transformers with weight-sharing -- not only exhibit similar expressive power but are also provably robust under mild assumptions. Besides out-of-distribution generalization, we also show that Looped Transformers are the only models that exhibit a monotonic behavior of loss with respect to depth.

A Little Help Goes a Long Way: Efficient LLM Training by Leveraging Small LMs

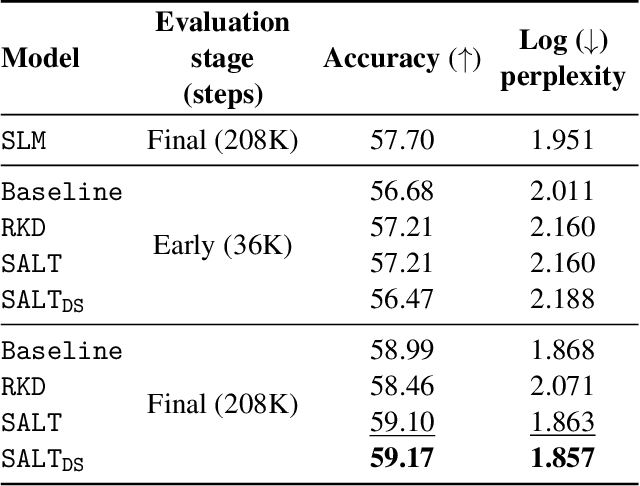
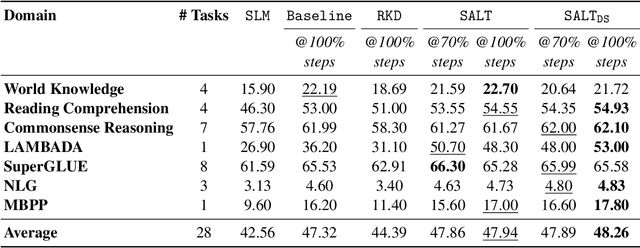
A primary challenge in large language model (LLM) development is their onerous pre-training cost. Typically, such pre-training involves optimizing a self-supervised objective (such as next-token prediction) over a large corpus. This paper explores a promising paradigm to improve LLM pre-training efficiency and quality by suitably leveraging a small language model (SLM). In particular, this paradigm relies on an SLM to both (1) provide soft labels as additional training supervision, and (2) select a small subset of valuable ("informative" and "hard") training examples. Put together, this enables an effective transfer of the SLM's predictive distribution to the LLM, while prioritizing specific regions of the training data distribution. Empirically, this leads to reduced LLM training time compared to standard training, while improving the overall quality. Theoretically, we develop a statistical framework to systematically study the utility of SLMs in enabling efficient training of high-quality LLMs. In particular, our framework characterizes how the SLM's seemingly low-quality supervision can enhance the training of a much more capable LLM. Furthermore, it also highlights the need for an adaptive utilization of such supervision, by striking a balance between the bias and variance introduced by the SLM-provided soft labels. We corroborate our theoretical framework by improving the pre-training of an LLM with 2.8B parameters by utilizing a smaller LM with 1.5B parameters on the Pile dataset.

Simplicity Bias via Global Convergence of Sharpness Minimization

The remarkable generalization ability of neural networks is usually attributed to the implicit bias of SGD, which often yields models with lower complexity using simpler (e.g. linear) and low-rank features. Recent works have provided empirical and theoretical evidence for the bias of particular variants of SGD (such as label noise SGD) toward flatter regions of the loss landscape. Despite the folklore intuition that flat solutions are 'simple', the connection with the simplicity of the final trained model (e.g. low-rank) is not well understood. In this work, we take a step toward bridging this gap by studying the simplicity structure that arises from minimizers of the sharpness for a class of two-layer neural networks. We show that, for any high dimensional training data and certain activations, with small enough step size, label noise SGD always converges to a network that replicates a single linear feature across all neurons; thereby, implying a simple rank one feature matrix. To obtain this result, our main technical contribution is to show that label noise SGD always minimizes the sharpness on the manifold of models with zero loss for two-layer networks. Along the way, we discover a novel property -- a local geodesic convexity -- of the trace of Hessian of the loss at approximate stationary points on the manifold of zero loss, which links sharpness to the geometry of the manifold. This tool may be of independent interest.

Can Looped Transformers Learn to Implement Multi-step Gradient Descent for In-context Learning?

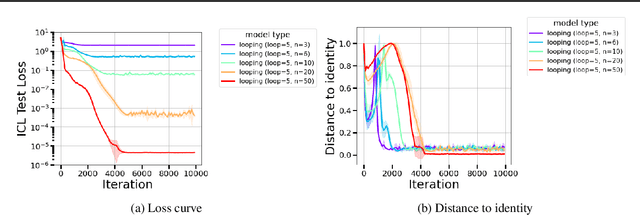
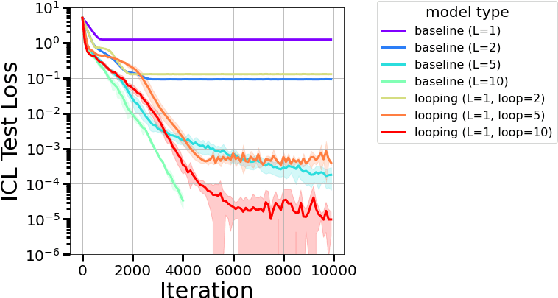
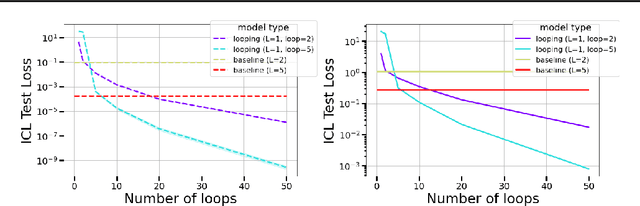
The remarkable capability of Transformers to do reasoning and few-shot learning, without any fine-tuning, is widely conjectured to stem from their ability to implicitly simulate a multi-step algorithms -- such as gradient descent -- with their weights in a single forward pass. Recently, there has been progress in understanding this complex phenomenon from an expressivity point of view, by demonstrating that Transformers can express such multi-step algorithms. However, our knowledge about the more fundamental aspect of its learnability, beyond single layer models, is very limited. In particular, can training Transformers enable convergence to algorithmic solutions? In this work we resolve this for in-context linear regression with linear looped Transformers -- a multi-layer model with weight sharing that is conjectured to have an inductive bias to learn fix-point iterative algorithms. More specifically, for this setting we show that the global minimizer of the population training loss implements multi-step preconditioned gradient descent, with a preconditioner that adapts to the data distribution. Furthermore, we show a fast convergence for gradient flow on the regression loss, despite the non-convexity of the landscape, by proving a novel gradient dominance condition. To our knowledge, this is the first theoretical analysis for multi-layer Transformer in this setting. We further validate our theoretical findings through synthetic experiments.

On the Inductive Bias of Stacking Towards Improving Reasoning

Given the increasing scale of model sizes, novel training strategies like gradual stacking [Gong et al., 2019, Reddi et al., 2023] have garnered interest. Stacking enables efficient training by gradually growing the depth of a model in stages and using layers from a smaller model in an earlier stage to initialize the next stage. Although efficient for training, the model biases induced by such growing approaches are largely unexplored. In this work, we examine this fundamental aspect of gradual stacking, going beyond its efficiency benefits. We propose a variant of gradual stacking called MIDAS that can speed up language model training by up to 40%. Furthermore we discover an intriguing phenomenon: MIDAS is not only training-efficient but surprisingly also has an inductive bias towards improving downstream tasks, especially tasks that require reasoning abilities like reading comprehension and math problems, despite having similar or slightly worse perplexity compared to baseline training. To further analyze this inductive bias, we construct reasoning primitives -- simple synthetic tasks that are building blocks for reasoning -- and find that a model pretrained with stacking is significantly better than standard pretraining on these primitives, with and without fine-tuning. This provides stronger and more robust evidence for this inductive bias towards reasoning. These findings of training efficiency and inductive bias towards reasoning are verified at 1B, 2B and 8B parameter language models. Finally, we conjecture the underlying reason for this inductive bias by exploring the connection of stacking to looped models and provide strong supporting empirical analysis.

Efficient Document Ranking with Learnable Late Interactions

Cross-Encoder (CE) and Dual-Encoder (DE) models are two fundamental approaches for query-document relevance in information retrieval. To predict relevance, CE models use joint query-document embeddings, while DE models maintain factorized query and document embeddings; usually, the former has higher quality while the latter benefits from lower latency. Recently, late-interaction models have been proposed to realize more favorable latency-quality tradeoffs, by using a DE structure followed by a lightweight scorer based on query and document token embeddings. However, these lightweight scorers are often hand-crafted, and there is no understanding of their approximation power; further, such scorers require access to individual document token embeddings, which imposes an increased latency and storage burden. In this paper, we propose novel learnable late-interaction models (LITE) that resolve these issues. Theoretically, we prove that LITE is a universal approximator of continuous scoring functions, even for relatively small embedding dimension. Empirically, LITE outperforms previous late-interaction models such as ColBERT on both in-domain and zero-shot re-ranking tasks. For instance, experiments on MS MARCO passage re-ranking show that LITE not only yields a model with better generalization, but also lowers latency and requires 0.25x storage compared to ColBERT.

Landscape-Aware Growing: The Power of a Little LAG

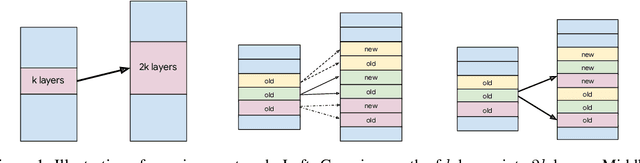
Recently, there has been increasing interest in efficient pretraining paradigms for training Transformer-based models. Several recent approaches use smaller models to initialize larger models in order to save computation (e.g., stacking and fusion). In this work, we study the fundamental question of how to select the best growing strategy from a given pool of growing strategies. Prior works have extensively focused on loss- and/or function-preserving behavior at initialization or simply performance at the end of training. Instead, we identify that behavior at initialization can be misleading as a predictor of final performance and present an alternative perspective based on early training dynamics, which we call "landscape-aware growing (LAG)". We perform extensive analysis of correlation of the final performance with performance in the initial steps of training and find early and more accurate predictions of the optimal growing strategy (i.e., with only a small "lag" after initialization). This perspective also motivates an adaptive strategy for gradual stacking.

Depth Dependence of $μ$P Learning Rates in ReLU MLPs

In this short note we consider random fully connected ReLU networks of width $n$ and depth $L$ equipped with a mean-field weight initialization. Our purpose is to study the dependence on $n$ and $L$ of the maximal update ($\mu$P) learning rate, the largest learning rate for which the mean squared change in pre-activations after one step of gradient descent remains uniformly bounded at large $n,L$. As in prior work on $\mu$P of Yang et. al., we find that this maximal update learning rate is independent of $n$ for all but the first and last layer weights. However, we find that it has a non-trivial dependence of $L$, scaling like $L^{-3/2}.$

Differentially Private Adaptive Optimization with Delayed Preconditioners

Privacy noise may negate the benefits of using adaptive optimizers in differentially private model training. Prior works typically address this issue by using auxiliary information (e.g., public data) to boost the effectiveness of adaptive optimization. In this work, we explore techniques to estimate and efficiently adapt to gradient geometry in private adaptive optimization without auxiliary data. Motivated by the observation that adaptive methods can tolerate stale preconditioners, we propose differentially private adaptive training with delayed preconditioners (DP^2), a simple method that constructs delayed but less noisy preconditioners to better realize the benefits of adaptivity. Theoretically, we provide convergence guarantees for our method for both convex and non-convex problems, and analyze trade-offs between delay and privacy noise reduction. Empirically, we explore DP^2 across several real-world datasets, demonstrating that it can improve convergence speed by as much as 4x relative to non-adaptive baselines and match the performance of state-of-the-art optimization methods that require auxiliary data.

On the Algorithmic Stability and Generalization of Adaptive Optimization Methods

Despite their popularity in deep learning and machine learning in general, the theoretical properties of adaptive optimizers such as Adagrad, RMSProp, Adam or AdamW are not yet fully understood. In this paper, we develop a novel framework to study the stability and generalization of these optimization methods. Based on this framework, we show provable guarantees about such properties that depend heavily on a single parameter $\beta_2$. Our empirical experiments support our claims and provide practical insights into the stability and generalization properties of adaptive optimization methods.