On the Role of Depth and Looping for In-Context Learning with Task Diversity

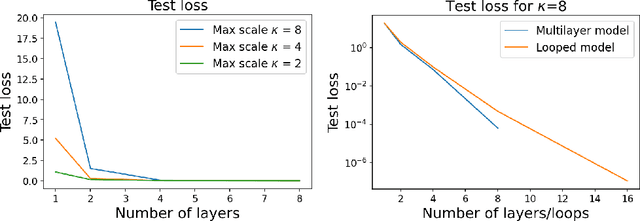
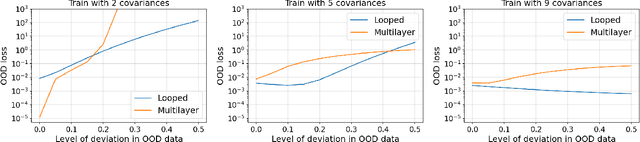
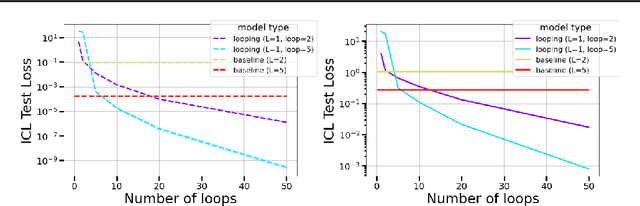
The intriguing in-context learning (ICL) abilities of deep Transformer models have lately garnered significant attention. By studying in-context linear regression on unimodal Gaussian data, recent empirical and theoretical works have argued that ICL emerges from Transformers' abilities to simulate learning algorithms like gradient descent. However, these works fail to capture the remarkable ability of Transformers to learn multiple tasks in context. To this end, we study in-context learning for linear regression with diverse tasks, characterized by data covariance matrices with condition numbers ranging from $[1, \kappa]$, and highlight the importance of depth in this setting. More specifically, (a) we show theoretical lower bounds of $\log(\kappa)$ (or $\sqrt{\kappa}$) linear attention layers in the unrestricted (or restricted) attention setting and, (b) we show that multilayer Transformers can indeed solve such tasks with a number of layers that matches the lower bounds. However, we show that this expressivity of multilayer Transformer comes at the price of robustness. In particular, multilayer Transformers are not robust to even distributional shifts as small as $O(e^{-L})$ in Wasserstein distance, where $L$ is the depth of the network. We then demonstrate that Looped Transformers -- a special class of multilayer Transformers with weight-sharing -- not only exhibit similar expressive power but are also provably robust under mild assumptions. Besides out-of-distribution generalization, we also show that Looped Transformers are the only models that exhibit a monotonic behavior of loss with respect to depth.

Computing Optimal Regularizers for Online Linear Optimization

Follow-the-Regularized-Leader (FTRL) algorithms are a popular class of learning algorithms for online linear optimization (OLO) that guarantee sub-linear regret, but the choice of regularizer can significantly impact dimension-dependent factors in the regret bound. We present an algorithm that takes as input convex and symmetric action sets and loss sets for a specific OLO instance, and outputs a regularizer such that running FTRL with this regularizer guarantees regret within a universal constant factor of the best possible regret bound. In particular, for any choice of (convex, symmetric) action set and loss set we prove that there exists an instantiation of FTRL which achieves regret within a constant factor of the best possible learning algorithm, strengthening the universality result of Srebro et al., 2011. Our algorithm requires preprocessing time and space exponential in the dimension $d$ of the OLO instance, but can be run efficiently online assuming a membership and linear optimization oracle for the action and loss sets, respectively (and is fully polynomial time for the case of constant dimension $d$). We complement this with a lower bound showing that even deciding whether a given regularizer is $\alpha$-strongly-convex with respect to a given norm is NP-hard.

Simplicity Bias via Global Convergence of Sharpness Minimization

The remarkable generalization ability of neural networks is usually attributed to the implicit bias of SGD, which often yields models with lower complexity using simpler (e.g. linear) and low-rank features. Recent works have provided empirical and theoretical evidence for the bias of particular variants of SGD (such as label noise SGD) toward flatter regions of the loss landscape. Despite the folklore intuition that flat solutions are 'simple', the connection with the simplicity of the final trained model (e.g. low-rank) is not well understood. In this work, we take a step toward bridging this gap by studying the simplicity structure that arises from minimizers of the sharpness for a class of two-layer neural networks. We show that, for any high dimensional training data and certain activations, with small enough step size, label noise SGD always converges to a network that replicates a single linear feature across all neurons; thereby, implying a simple rank one feature matrix. To obtain this result, our main technical contribution is to show that label noise SGD always minimizes the sharpness on the manifold of models with zero loss for two-layer networks. Along the way, we discover a novel property -- a local geodesic convexity -- of the trace of Hessian of the loss at approximate stationary points on the manifold of zero loss, which links sharpness to the geometry of the manifold. This tool may be of independent interest.

Can Looped Transformers Learn to Implement Multi-step Gradient Descent for In-context Learning?

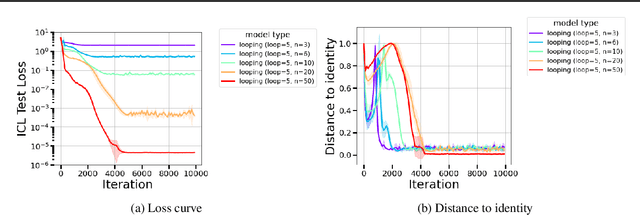
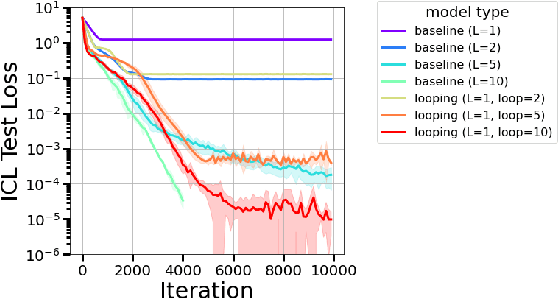
The remarkable capability of Transformers to do reasoning and few-shot learning, without any fine-tuning, is widely conjectured to stem from their ability to implicitly simulate a multi-step algorithms -- such as gradient descent -- with their weights in a single forward pass. Recently, there has been progress in understanding this complex phenomenon from an expressivity point of view, by demonstrating that Transformers can express such multi-step algorithms. However, our knowledge about the more fundamental aspect of its learnability, beyond single layer models, is very limited. In particular, can training Transformers enable convergence to algorithmic solutions? In this work we resolve this for in-context linear regression with linear looped Transformers -- a multi-layer model with weight sharing that is conjectured to have an inductive bias to learn fix-point iterative algorithms. More specifically, for this setting we show that the global minimizer of the population training loss implements multi-step preconditioned gradient descent, with a preconditioner that adapts to the data distribution. Furthermore, we show a fast convergence for gradient flow on the regression loss, despite the non-convexity of the landscape, by proving a novel gradient dominance condition. To our knowledge, this is the first theoretical analysis for multi-layer Transformer in this setting. We further validate our theoretical findings through synthetic experiments.

Adversarial Online Learning with Temporal Feedback Graphs

We study a variant of prediction with expert advice where the learner's action at round $t$ is only allowed to depend on losses on a specific subset of the rounds (where the structure of which rounds' losses are visible at time $t$ is provided by a directed "feedback graph" known to the learner). We present a novel learning algorithm for this setting based on a strategy of partitioning the losses across sub-cliques of this graph. We complement this with a lower bound that is tight in many practical settings, and which we conjecture to be within a constant factor of optimal. For the important class of transitive feedback graphs, we prove that this algorithm is efficiently implementable and obtains the optimal regret bound (up to a universal constant).

Learning Mixtures of Gaussians Using Diffusion Models

We give a new algorithm for learning mixtures of $k$ Gaussians (with identity covariance in $\mathbb{R}^n$) to TV error $\varepsilon$, with quasi-polynomial ($O(n^{\text{poly log}\left(\frac{n+k}{\varepsilon}\right)})$) time and sample complexity, under a minimum weight assumption. Unlike previous approaches, most of which are algebraic in nature, our approach is analytic and relies on the framework of diffusion models. Diffusion models are a modern paradigm for generative modeling, which typically rely on learning the score function (gradient log-pdf) along a process transforming a pure noise distribution, in our case a Gaussian, to the data distribution. Despite their dazzling performance in tasks such as image generation, there are few end-to-end theoretical guarantees that they can efficiently learn nontrivial families of distributions; we give some of the first such guarantees. We proceed by deriving higher-order Gaussian noise sensitivity bounds for the score functions for a Gaussian mixture to show that that they can be inductively learned using piecewise polynomial regression (up to poly-logarithmic degree), and combine this with known convergence results for diffusion models. Our results extend to continuous mixtures of Gaussians where the mixing distribution is supported on a union of $k$ balls of constant radius. In particular, this applies to the case of Gaussian convolutions of distributions on low-dimensional manifolds, or more generally sets with small covering number.

EM for Mixture of Linear Regression with Clustered Data

Modern data-driven and distributed learning frameworks deal with diverse massive data generated by clients spread across heterogeneous environments. Indeed, data heterogeneity is a major bottleneck in scaling up many distributed learning paradigms. In many settings however, heterogeneous data may be generated in clusters with shared structures, as is the case in several applications such as federated learning where a common latent variable governs the distribution of all the samples generated by a client. It is therefore natural to ask how the underlying clustered structures in distributed data can be exploited to improve learning schemes. In this paper, we tackle this question in the special case of estimating $d$-dimensional parameters of a two-component mixture of linear regressions problem where each of $m$ nodes generates $n$ samples with a shared latent variable. We employ the well-known Expectation-Maximization (EM) method to estimate the maximum likelihood parameters from $m$ batches of dependent samples each containing $n$ measurements. Discarding the clustered structure in the mixture model, EM is known to require $O(\log(mn/d))$ iterations to reach the statistical accuracy of $O(\sqrt{d/(mn)})$. In contrast, we show that if initialized properly, EM on the structured data requires only $O(1)$ iterations to reach the same statistical accuracy, as long as $m$ grows up as $e^{o(n)}$. Our analysis establishes and combines novel asymptotic optimization and generalization guarantees for population and empirical EM with dependent samples, which may be of independent interest.

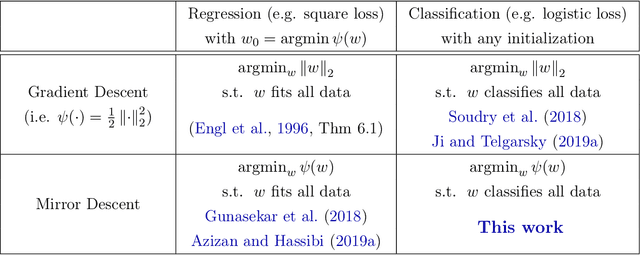
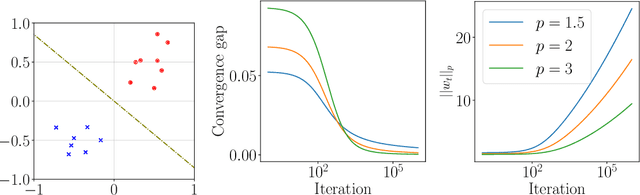
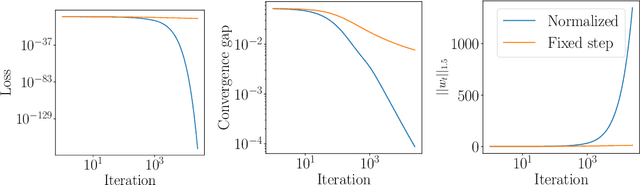
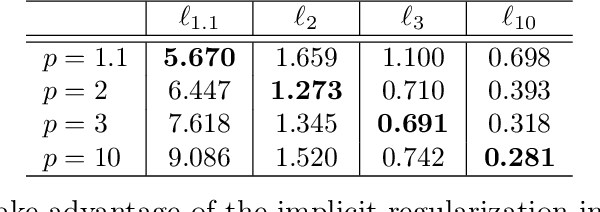
A Unified Approach to Controlling Implicit Regularization via Mirror Descent

Inspired by the remarkable success of deep neural networks, there has been significant interest in understanding the generalization performance of overparameterized models. Substantial efforts have been invested in characterizing how optimization algorithms impact generalization through their "preferred" solutions, a phenomenon commonly referred to as implicit regularization. In particular, it has been argued that gradient descent (GD) induces an implicit $\ell_2$-norm regularization in regression and classification problems. However, the implicit regularization of different algorithms are confined to either a specific geometry or a particular class of learning problems, indicating a gap in a general approach for controlling the implicit regularization. To address this, we present a unified approach using mirror descent (MD), a notable generalization of GD, to control implicit regularization in both regression and classification settings. More specifically, we show that MD with the general class of homogeneous potential functions converges in direction to a generalized maximum-margin solution for linear classification problems, thereby answering a long-standing question in the classification setting. Further, we show that MD can be implemented efficiently and under suitable conditions, enjoys fast convergence. Through comprehensive experiments, we demonstrate that MD is a versatile method to produce learned models with different regularizers, which in turn have different generalization performances.

The Inductive Bias of Flatness Regularization for Deep Matrix Factorization

Recent works on over-parameterized neural networks have shown that the stochasticity in optimizers has the implicit regularization effect of minimizing the sharpness of the loss function (in particular, the trace of its Hessian) over the family zero-loss solutions. More explicit forms of flatness regularization also empirically improve the generalization performance. However, it remains unclear why and when flatness regularization leads to better generalization. This work takes the first step toward understanding the inductive bias of the minimum trace of the Hessian solutions in an important setting: learning deep linear networks from linear measurements, also known as \emph{deep matrix factorization}. We show that for all depth greater than one, with the standard Restricted Isometry Property (RIP) on the measurements, minimizing the trace of Hessian is approximately equivalent to minimizing the Schatten 1-norm of the corresponding end-to-end matrix parameters (i.e., the product of all layer matrices), which in turn leads to better generalization. We empirically verify our theoretical findings on synthetic datasets.

Projection-Free Online Convex Optimization via Efficient Newton Iterations

This paper presents new projection-free algorithms for Online Convex Optimization (OCO) over a convex domain $\mathcal{K} \subset \mathbb{R}^d$. Classical OCO algorithms (such as Online Gradient Descent) typically need to perform Euclidean projections onto the convex set $\cK$ to ensure feasibility of their iterates. Alternative algorithms, such as those based on the Frank-Wolfe method, swap potentially-expensive Euclidean projections onto $\mathcal{K}$ for linear optimization over $\mathcal{K}$. However, such algorithms have a sub-optimal regret in OCO compared to projection-based algorithms. In this paper, we look at a third type of algorithms that output approximate Newton iterates using a self-concordant barrier for the set of interest. The use of a self-concordant barrier automatically ensures feasibility without the need for projections. However, the computation of the Newton iterates requires a matrix inverse, which can still be expensive. As our main contribution, we show how the stability of the Newton iterates can be leveraged to compute the inverse Hessian only a vanishing fraction of the rounds, leading to a new efficient projection-free OCO algorithm with a state-of-the-art regret bound.