Structured Preconditioners in Adaptive Optimization: A Unified Analysis

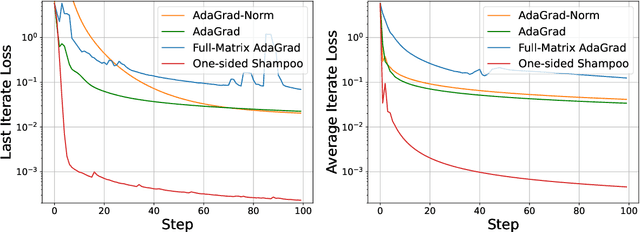
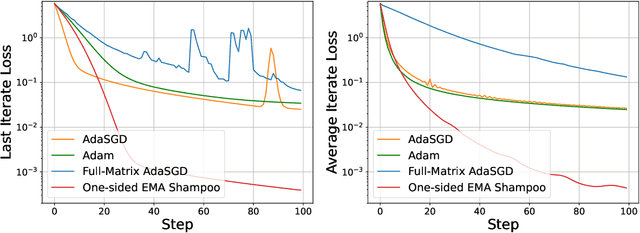
We present a novel unified analysis for a broad class of adaptive optimization algorithms with structured (e.g., layerwise, diagonal, and kronecker-factored) preconditioners for both online regret minimization and offline convex optimization. Our analysis not only provides matching rate to several important structured preconditioned algorithms including diagonal AdaGrad, full-matrix AdaGrad, and AdaGrad-Norm, but also gives an improved convergence rate for a one-sided variant of Shampoo over that of original Shampoo. Interestingly, more structured preconditioners (e.g., diagonal Adagrad, AdaGrad-Norm which use less space and compute) are often presented as computationally efficient approximations to full-matrix Adagrad, aiming for improved optimization performance through better approximations. Our unified analysis challenges this prevailing view and reveals, perhaps surprisingly, that more structured preconditioners, despite using less space and computation per step, can outperform their less structured counterparts. To demonstrate this, we show that one-sided Shampoo, which is relatively much cheaper than full-matrix AdaGrad could outperform it both theoretically and experimentally.

Efficient Stagewise Pretraining via Progressive Subnetworks

Recent developments in large language models have sparked interest in efficient pretraining methods. A recent effective paradigm is to perform stage-wise training, where the size of the model is gradually increased over the course of training (e.g. gradual stacking (Reddi et al., 2023)). While the resource and wall-time savings are appealing, it has limitations, particularly the inability to evaluate the full model during earlier stages, and degradation in model quality due to smaller model capacity in the initial stages. In this work, we propose an alternative framework, progressive subnetwork training, that maintains the full model throughout training, but only trains subnetworks within the model in each step. We focus on a simple instantiation of this framework, Random Path Training (RaPTr) that only trains a sub-path of layers in each step, progressively increasing the path lengths in stages. RaPTr achieves better pre-training loss for BERT and UL2 language models while requiring 20-33% fewer FLOPs compared to standard training, and is competitive or better than other efficient training methods. Furthermore, RaPTr shows better downstream performance on UL2, improving QA tasks and SuperGLUE by 1-5% compared to standard training and stacking. Finally, we provide a theoretical basis for RaPTr to justify (a) the increasing complexity of subnetworks in stages, and (b) the stability in loss across stage transitions due to residual connections and layer norm.

The Inductive Bias of Flatness Regularization for Deep Matrix Factorization

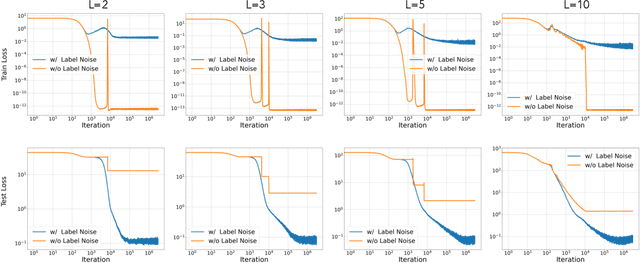
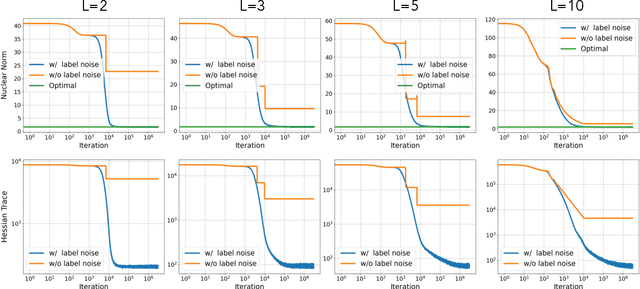
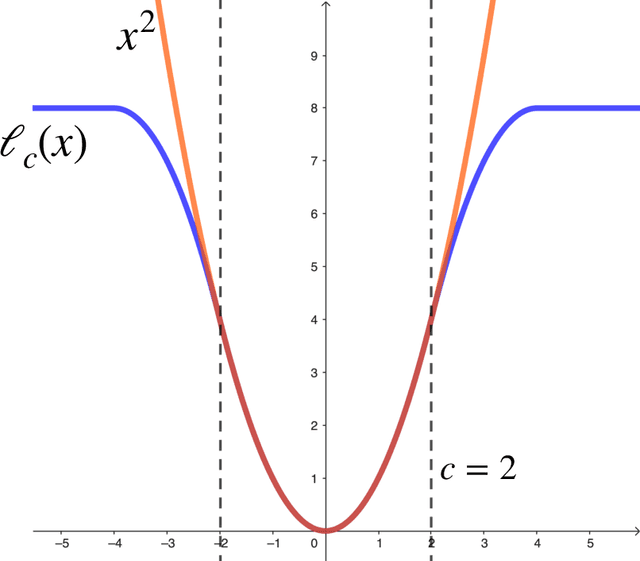
Recent works on over-parameterized neural networks have shown that the stochasticity in optimizers has the implicit regularization effect of minimizing the sharpness of the loss function (in particular, the trace of its Hessian) over the family zero-loss solutions. More explicit forms of flatness regularization also empirically improve the generalization performance. However, it remains unclear why and when flatness regularization leads to better generalization. This work takes the first step toward understanding the inductive bias of the minimum trace of the Hessian solutions in an important setting: learning deep linear networks from linear measurements, also known as \emph{deep matrix factorization}. We show that for all depth greater than one, with the standard Restricted Isometry Property (RIP) on the measurements, minimizing the trace of Hessian is approximately equivalent to minimizing the Schatten 1-norm of the corresponding end-to-end matrix parameters (i.e., the product of all layer matrices), which in turn leads to better generalization. We empirically verify our theoretical findings on synthetic datasets.

FedLite: A Scalable Approach for Federated Learning on Resource-constrained Clients

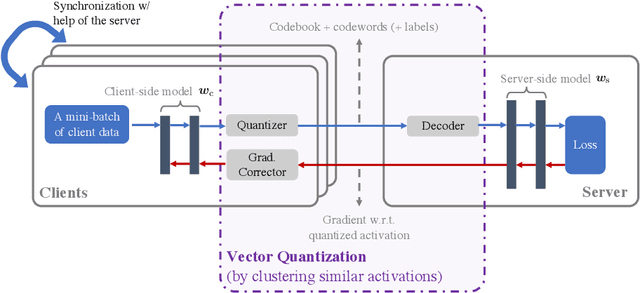
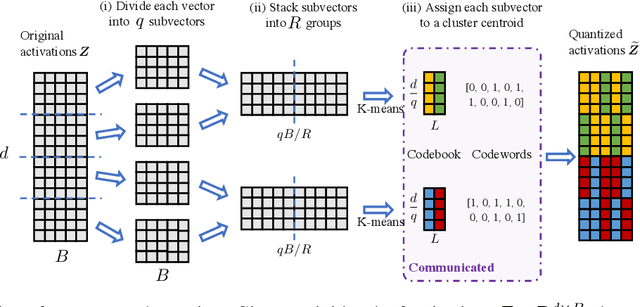
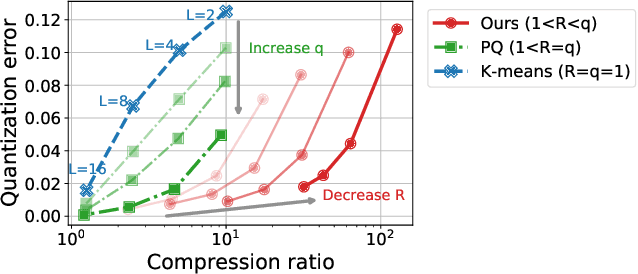
In classical federated learning, the clients contribute to the overall training by communicating local updates for the underlying model on their private data to a coordinating server. However, updating and communicating the entire model becomes prohibitively expensive when resource-constrained clients collectively aim to train a large machine learning model. Split learning provides a natural solution in such a setting, where only a small part of the model is stored and trained on clients while the remaining large part of the model only stays at the servers. However, the model partitioning employed in split learning introduces a significant amount of communication cost. This paper addresses this issue by compressing the additional communication using a novel clustering scheme accompanied by a gradient correction method. Extensive empirical evaluations on image and text benchmarks show that the proposed method can achieve up to $490\times$ communication cost reduction with minimal drop in accuracy, and enables a desirable performance vs. communication trade-off.

Disentangling Sampling and Labeling Bias for Learning in Large-Output Spaces

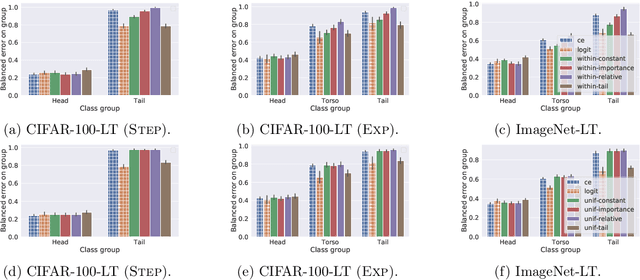
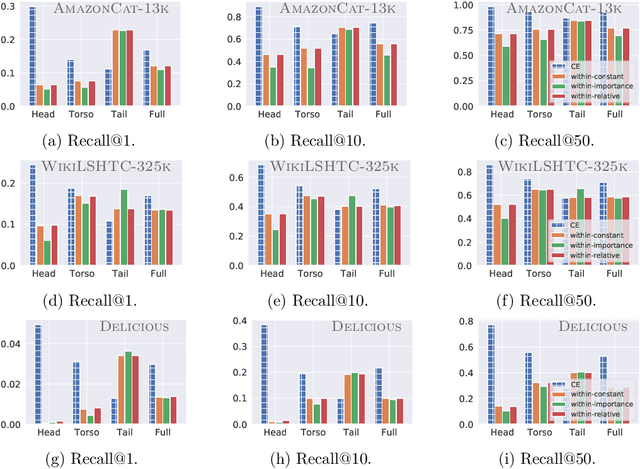
Negative sampling schemes enable efficient training given a large number of classes, by offering a means to approximate a computationally expensive loss function that takes all labels into account. In this paper, we present a new connection between these schemes and loss modification techniques for countering label imbalance. We show that different negative sampling schemes implicitly trade-off performance on dominant versus rare labels. Further, we provide a unified means to explicitly tackle both sampling bias, arising from working with a subset of all labels, and labeling bias, which is inherent to the data due to label imbalance. We empirically verify our findings on long-tail classification and retrieval benchmarks.

Federated Composite Optimization

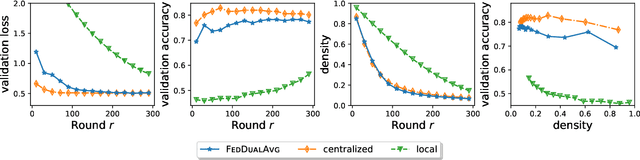
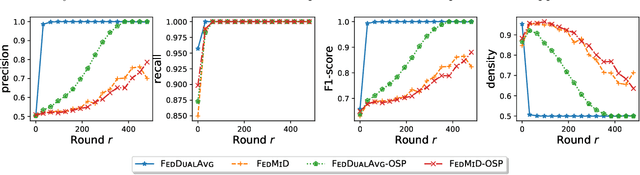
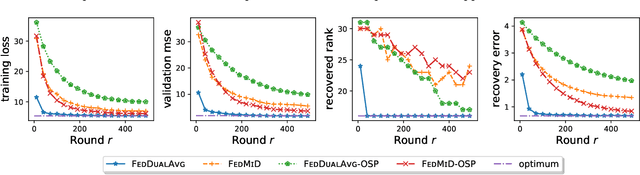
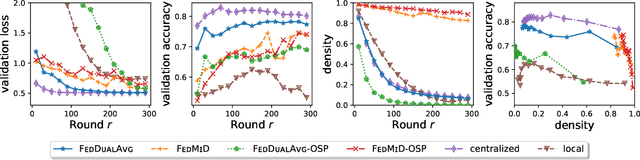
Federated Learning (FL) is a distributed learning paradigm which scales on-device learning collaboratively and privately. Standard FL algorithms such as Federated Averaging (FedAvg) are primarily geared towards smooth unconstrained settings. In this paper, we study the Federated Composite Optimization (FCO) problem, where the objective function in FL includes an additive (possibly) non-smooth component. Such optimization problems are fundamental to machine learning and arise naturally in the context of regularization (e.g., sparsity, low-rank, monotonicity, and constraint). To tackle this problem, we propose different primal/dual averaging approaches and study their communication and computation complexities. Of particular interest is Federated Dual Averaging (FedDualAvg), a federated variant of the dual averaging algorithm. FedDualAvg uses a novel double averaging procedure, which involves gradient averaging step in standard dual averaging and an average of client updates akin to standard federated averaging. Our theoretical analysis and empirical experiments demonstrate that FedDualAvg outperforms baselines for FCO.

Adaptive Federated Optimization

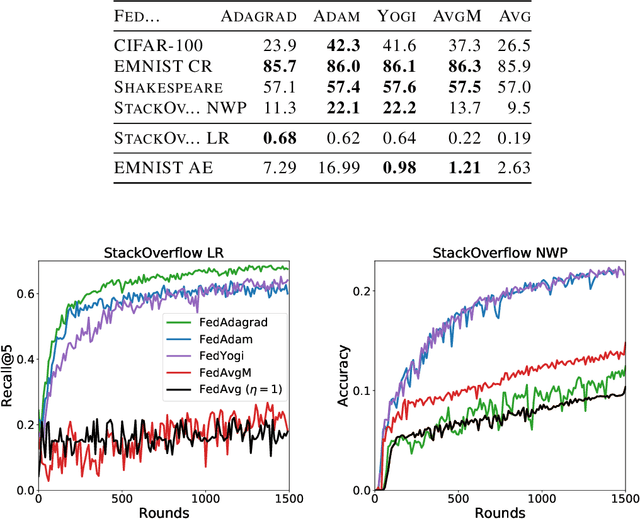
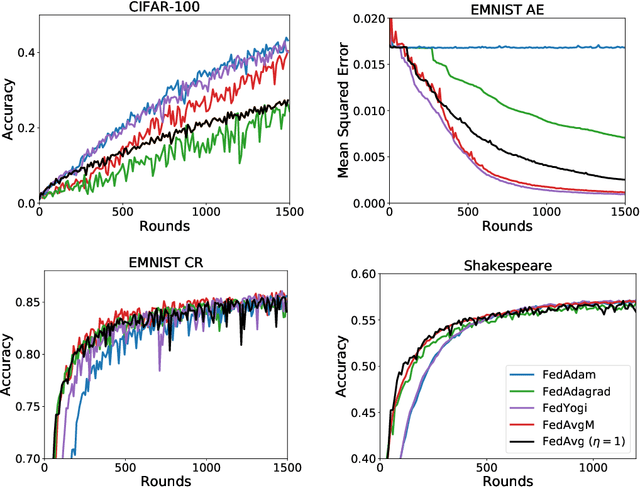
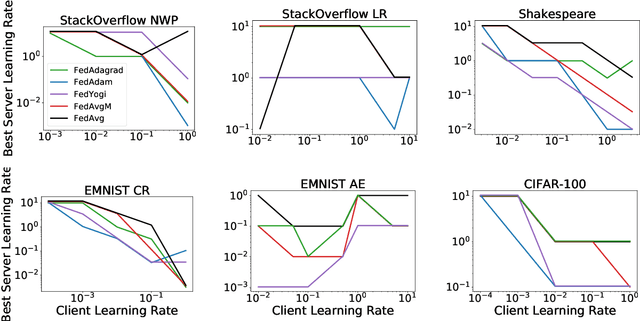
Federated learning is a distributed machine learning paradigm in which a large number of clients coordinate with a central server to learn a model without sharing their own training data. Due to the heterogeneity of the client datasets, standard federated optimization methods such as Federated Averaging (FedAvg) are often difficult to tune and exhibit unfavorable convergence behavior. In non-federated settings, adaptive optimization methods have had notable success in combating such issues. In this work, we propose federated versions of adaptive optimizers, including Adagrad, Adam, and Yogi, and analyze their convergence in the presence of heterogeneous data for general nonconvex settings. Our results highlight the interplay between client heterogeneity and communication efficiency. We also perform extensive experiments on these methods and show that the use of adaptive optimizers can significantly improve the performance of federated learning.

Adaptive Sampling Distributed Stochastic Variance Reduced Gradient for Heterogeneous Distributed Datasets

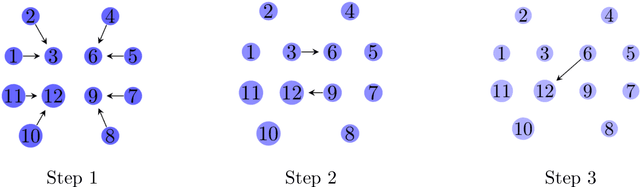
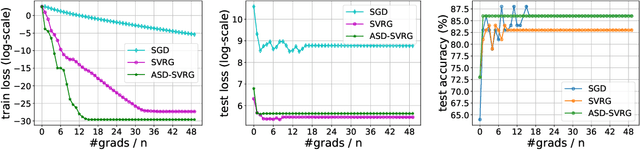
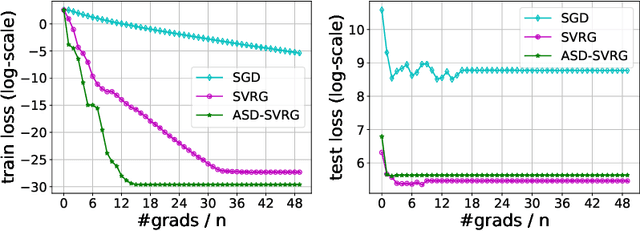
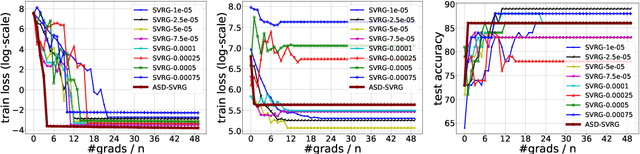
We study distributed optimization algorithms for minimizing the average of \emph{heterogeneous} functions distributed across several machines with a focus on communication efficiency. In such settings, naively using the classical stochastic gradient descent (SGD) or its variants (e.g., SVRG) with a uniform sampling of machines typically yields poor performance. It often leads to the dependence of convergence rate on maximum Lipschitz constant of gradients across the devices. In this paper, we propose a novel \emph{adaptive} sampling of machines specially catered to these settings. Our method relies on an adaptive estimate of local Lipschitz constants base on the information of past gradients. We show that the new way improves the dependence of convergence rate from maximum Lipschitz constant to \emph{average} Lipschitz constant across machines, thereby, significantly accelerating the convergence. Our experiments demonstrate that our method indeed speeds up the convergence of the standard SVRG algorithm in heterogeneous environments.

Learning to Learn by Zeroth-Order Oracle

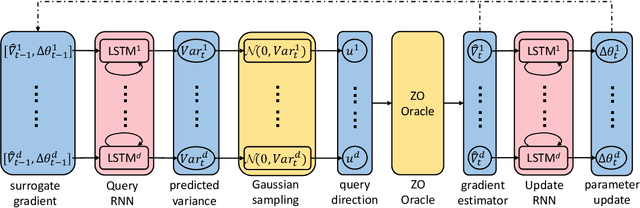
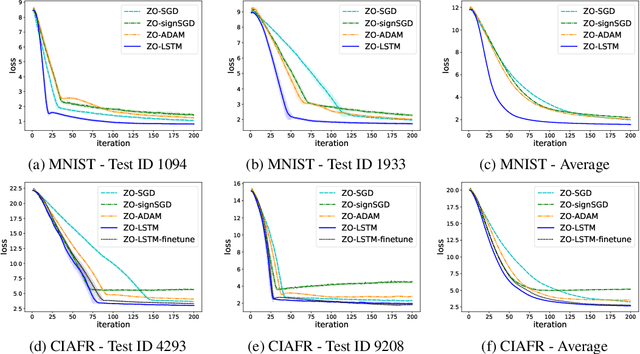
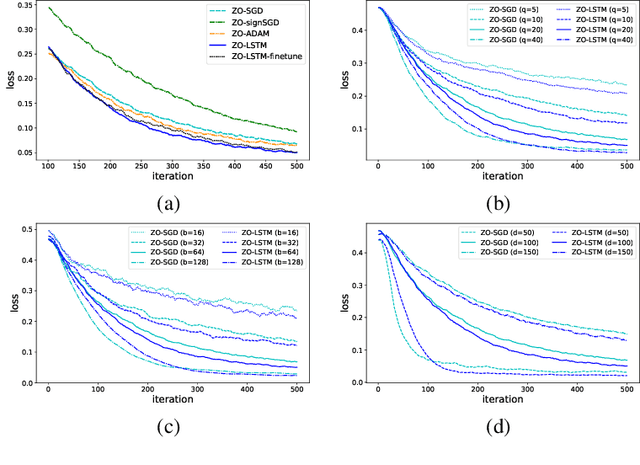
In the learning to learn (L2L) framework, we cast the design of optimization algorithms as a machine learning problem and use deep neural networks to learn the update rules. In this paper, we extend the L2L framework to zeroth-order (ZO) optimization setting, where no explicit gradient information is available. Our learned optimizer, modeled as recurrent neural network (RNN), first approximates gradient by ZO gradient estimator and then produces parameter update utilizing the knowledge of previous iterations. To reduce high variance effect due to ZO gradient estimator, we further introduce another RNN to learn the Gaussian sampling rule and dynamically guide the query direction sampling. Our learned optimizer outperforms hand-designed algorithms in terms of convergence rate and final solution on both synthetic and practical ZO optimization tasks (in particular, the black-box adversarial attack task, which is one of the most widely used tasks of ZO optimization). We finally conduct extensive analytical experiments to demonstrate the effectiveness of our proposed optimizer.

Large-scale randomized-coordinate descent methods with non-separable linear constraints

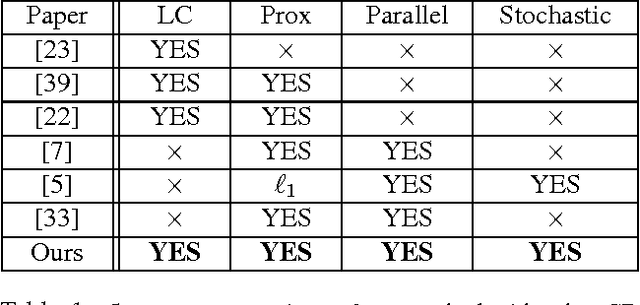
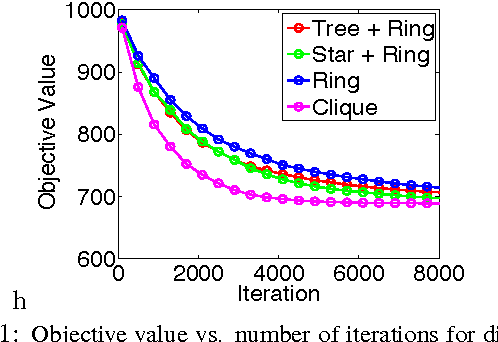
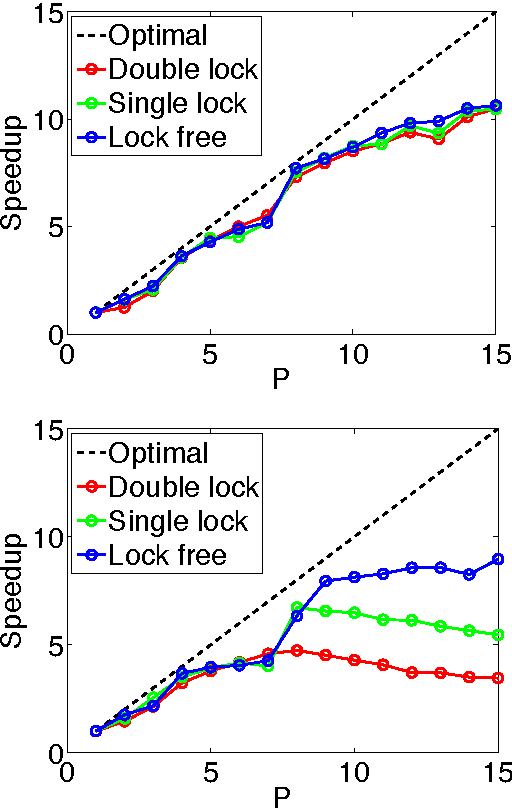
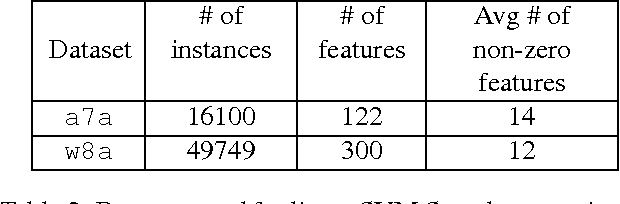
We develop randomized (block) coordinate descent (CD) methods for linearly constrained convex optimization. Unlike most CD methods, we do not assume the constraints to be separable, but let them be coupled linearly. To our knowledge, ours is the first CD method that allows linear coupling constraints, without making the global iteration complexity have an exponential dependence on the number of constraints. We present algorithms and analysis for four key problem scenarios: (i) smooth; (ii) smooth + nonsmooth separable; (iii) asynchronous parallel; and (iv) stochastic. We illustrate empirical behavior of our algorithms by simulation experiments.