Structured Preconditioners in Adaptive Optimization: A Unified Analysis
Paper and Code
Mar 13, 2025
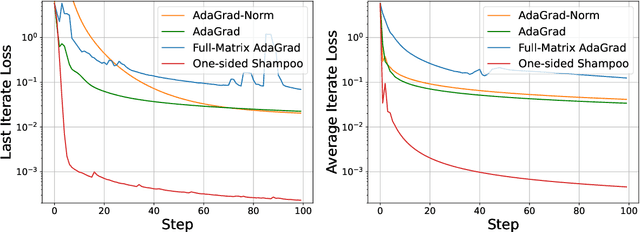

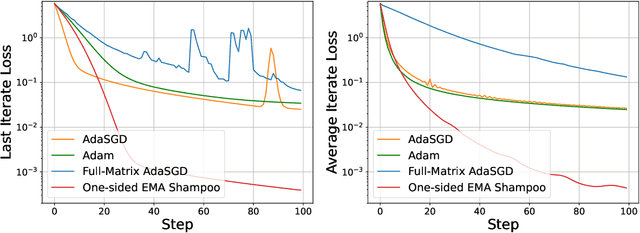
We present a novel unified analysis for a broad class of adaptive optimization algorithms with structured (e.g., layerwise, diagonal, and kronecker-factored) preconditioners for both online regret minimization and offline convex optimization. Our analysis not only provides matching rate to several important structured preconditioned algorithms including diagonal AdaGrad, full-matrix AdaGrad, and AdaGrad-Norm, but also gives an improved convergence rate for a one-sided variant of Shampoo over that of original Shampoo. Interestingly, more structured preconditioners (e.g., diagonal Adagrad, AdaGrad-Norm which use less space and compute) are often presented as computationally efficient approximations to full-matrix Adagrad, aiming for improved optimization performance through better approximations. Our unified analysis challenges this prevailing view and reveals, perhaps surprisingly, that more structured preconditioners, despite using less space and computation per step, can outperform their less structured counterparts. To demonstrate this, we show that one-sided Shampoo, which is relatively much cheaper than full-matrix AdaGrad could outperform it both theoretically and experimentally.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge