Large-scale randomized-coordinate descent methods with non-separable linear constraints
Paper and Code
Jun 10, 2015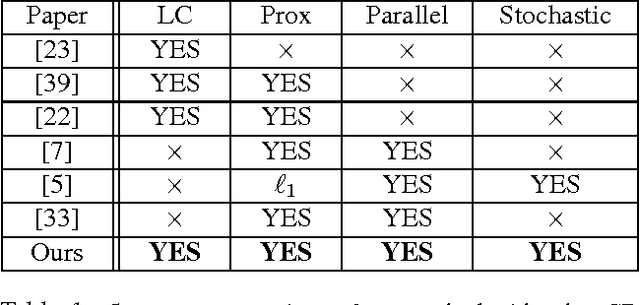
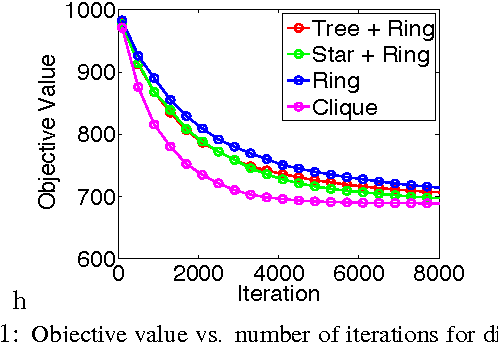
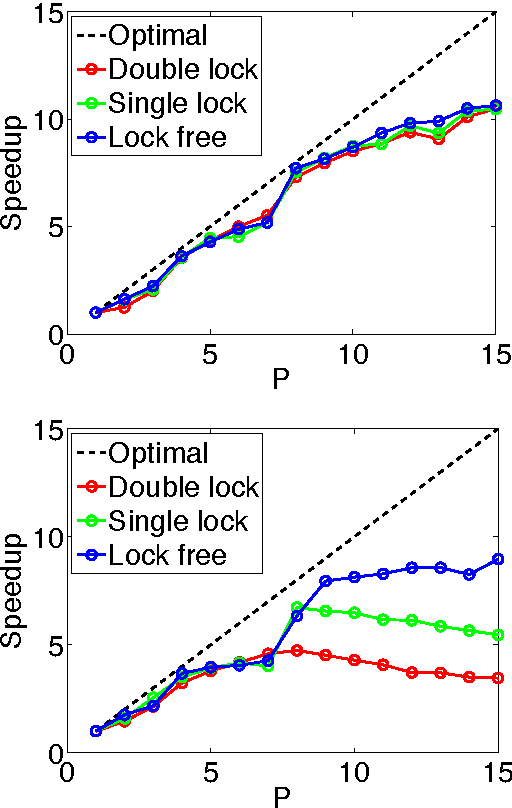
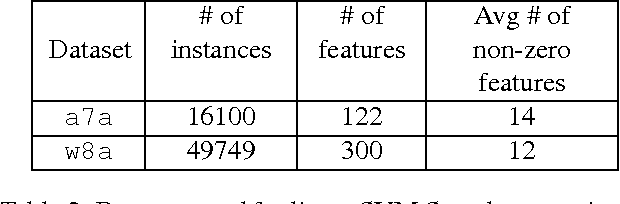
We develop randomized (block) coordinate descent (CD) methods for linearly constrained convex optimization. Unlike most CD methods, we do not assume the constraints to be separable, but let them be coupled linearly. To our knowledge, ours is the first CD method that allows linear coupling constraints, without making the global iteration complexity have an exponential dependence on the number of constraints. We present algorithms and analysis for four key problem scenarios: (i) smooth; (ii) smooth + nonsmooth separable; (iii) asynchronous parallel; and (iv) stochastic. We illustrate empirical behavior of our algorithms by simulation experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge