VN-Transformer: Rotation-Equivariant Attention for Vector Neurons

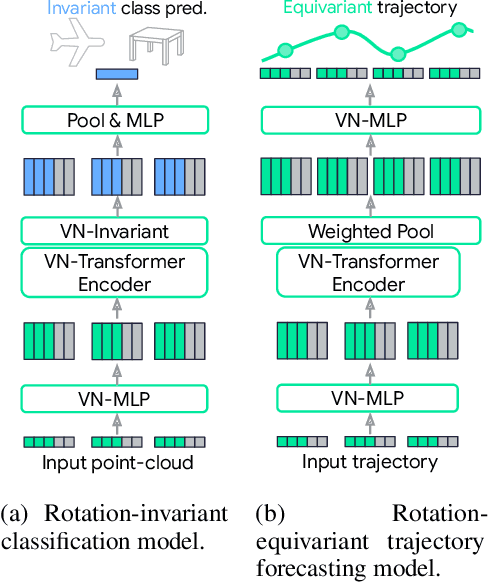
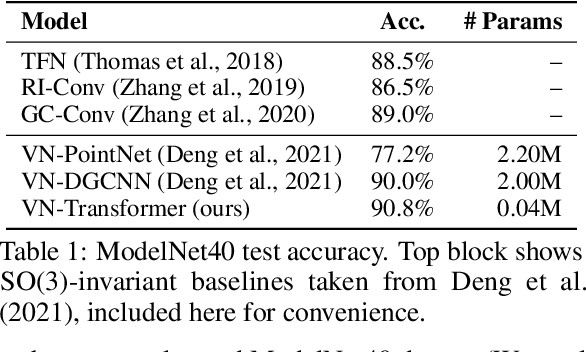
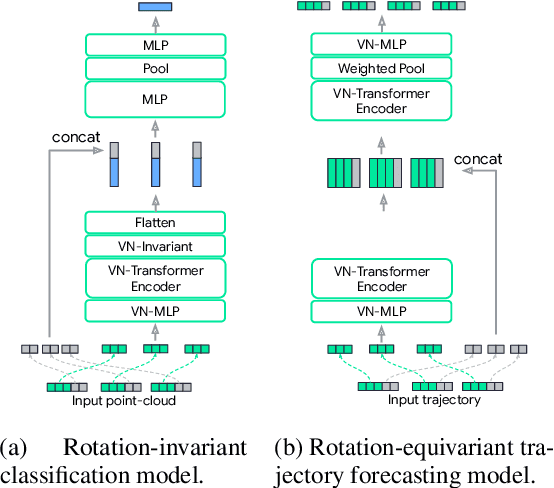
Rotation equivariance is a desirable property in many practical applications such as motion forecasting and 3D perception, where it can offer benefits like sample efficiency, better generalization, and robustness to input perturbations. Vector Neurons (VN) is a recently developed framework offering a simple yet effective approach for deriving rotation-equivariant analogs of standard machine learning operations by extending one-dimensional scalar neurons to three-dimensional "vector neurons." We introduce a novel "VN-Transformer" architecture to address several shortcomings of the current VN models. Our contributions are: $(i)$ we derive a rotation-equivariant attention mechanism which eliminates the need for the heavy feature preprocessing required by the original Vector Neurons models; $(ii)$ we extend the VN framework to support non-spatial attributes, expanding the applicability of these models to real-world datasets; $(iii)$ we derive a rotation-equivariant mechanism for multi-scale reduction of point-cloud resolution, greatly speeding up inference and training; $(iv)$ we show that small tradeoffs in equivariance ($\epsilon$-approximate equivariance) can be used to obtain large improvements in numerical stability and training robustness on accelerated hardware, and we bound the propagation of equivariance violations in our models. Finally, we apply our VN-Transformer to 3D shape classification and motion forecasting with compelling results.

Identifying Driver Interactions via Conditional Behavior Prediction

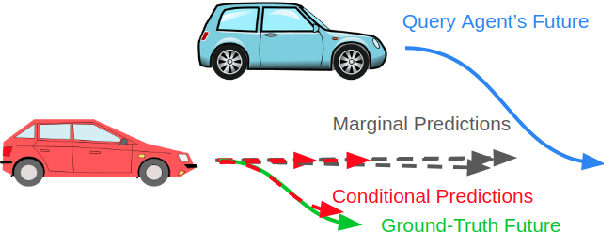
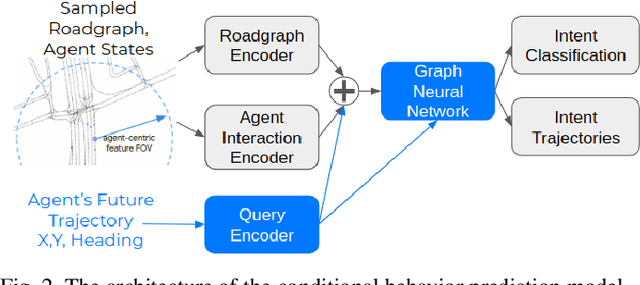
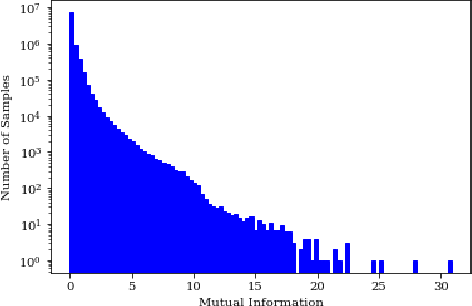
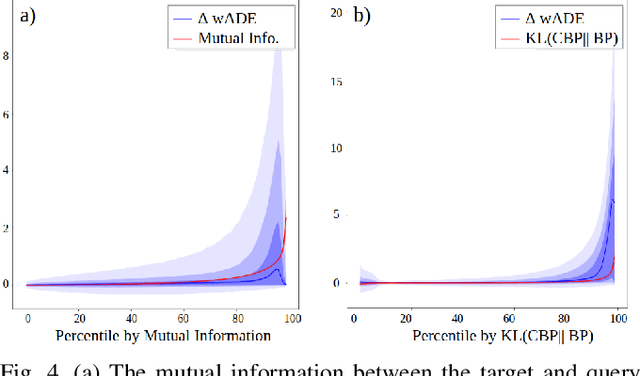
Interactive driving scenarios, such as lane changes, merges and unprotected turns, are some of the most challenging situations for autonomous driving. Planning in interactive scenarios requires accurately modeling the reactions of other agents to different future actions of the ego agent. We develop end-to-end models for conditional behavior prediction (CBP) that take as an input a query future trajectory for an ego-agent, and predict distributions over future trajectories for other agents conditioned on the query. Leveraging such a model, we develop a general-purpose agent interactivity score derived from probabilistic first principles. The interactivity score allows us to find interesting interactive scenarios for training and evaluating behavior prediction models. We further demonstrate that the proposed score is effective for agent prioritization under computational budget constraints.

Learning and Inference in Hilbert Space with Quantum Graphical Models

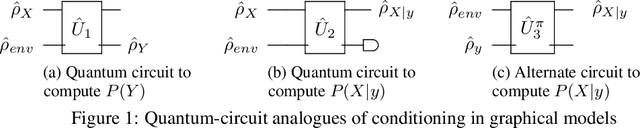
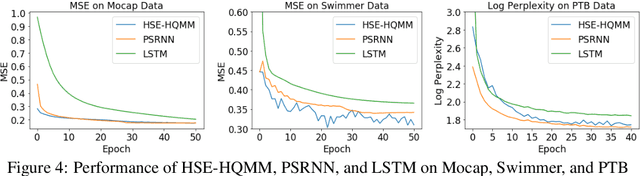
Quantum Graphical Models (QGMs) generalize classical graphical models by adopting the formalism for reasoning about uncertainty from quantum mechanics. Unlike classical graphical models, QGMs represent uncertainty with density matrices in complex Hilbert spaces. Hilbert space embeddings (HSEs) also generalize Bayesian inference in Hilbert spaces. We investigate the link between QGMs and HSEs and show that the sum rule and Bayes rule for QGMs are equivalent to the kernel sum rule in HSEs and a special case of Nadaraya-Watson kernel regression, respectively. We show that these operations can be kernelized, and use these insights to propose a Hilbert Space Embedding of Hidden Quantum Markov Models (HSE-HQMM) to model dynamics. We present experimental results showing that HSE-HQMMs are competitive with state-of-the-art models like LSTMs and PSRNNs on several datasets, while also providing a nonparametric method for maintaining a probability distribution over continuous-valued features.

An Efficient, Expressive and Local Minima-free Method for Learning Controlled Dynamical Systems

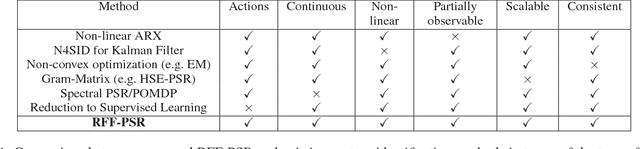
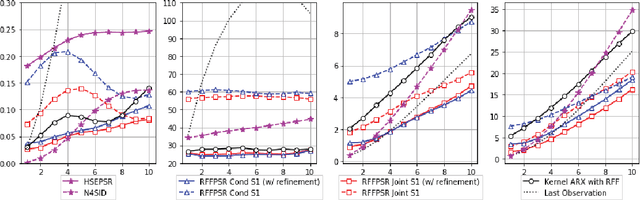
We propose a framework for modeling and estimating the state of controlled dynamical systems, where an agent can affect the system through actions and receives partial observations. Based on this framework, we propose the Predictive State Representation with Random Fourier Features (RFFPSR). A key property in RFF-PSRs is that the state estimate is represented by a conditional distribution of future observations given future actions. RFF-PSRs combine this representation with moment-matching, kernel embedding and local optimization to achieve a method that enjoys several favorable qualities: It can represent controlled environments which can be affected by actions; it has an efficient and theoretically justified learning algorithm; it uses a non-parametric representation that has expressive power to represent continuous non-linear dynamics. We provide a detailed formulation, a theoretical analysis and an experimental evaluation that demonstrates the effectiveness of our method.

Speaker Diarization with LSTM

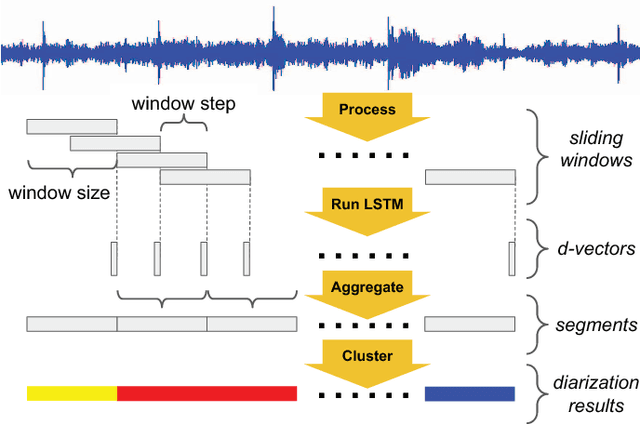
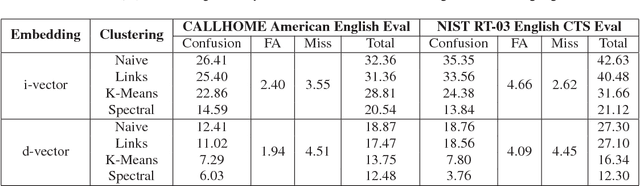
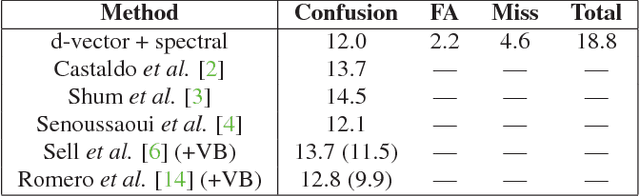
For many years, i-vector based audio embedding techniques were the dominant approach for speaker verification and speaker diarization applications. However, mirroring the rise of deep learning in various domains, neural network based audio embeddings, also known as d-vectors, have consistently demonstrated superior speaker verification performance. In this paper, we build on the success of d-vector based speaker verification systems to develop a new d-vector based approach to speaker diarization. Specifically, we combine LSTM-based d-vector audio embeddings with recent work in non-parametric clustering to obtain a state-of-the-art speaker diarization system. Our system is evaluated on three standard public datasets, suggesting that d-vector based diarization systems offer significant advantages over traditional i-vector based systems. We achieved a 12.0% diarization error rate on NIST SRE 2000 CALLHOME, while our model is trained with out-of-domain data from voice search logs.

Links: A High-Dimensional Online Clustering Method

We present a novel algorithm, called Links, designed to perform online clustering on unit vectors in a high-dimensional Euclidean space. The algorithm is appropriate when it is necessary to cluster data efficiently as it streams in, and is to be contrasted with traditional batch clustering algorithms that have access to all data at once. For example, Links has been successfully applied to embedding vectors generated from face images or voice recordings for the purpose of recognizing people, thereby providing real-time identification during video or audio capture.

Predictive State Recurrent Neural Networks

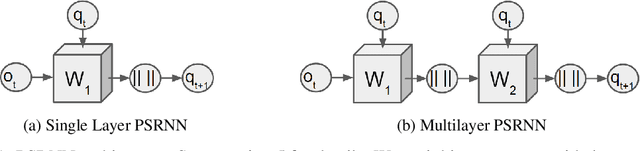
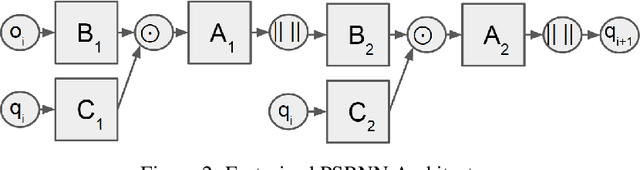
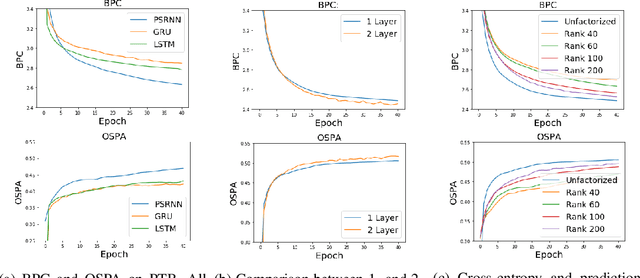
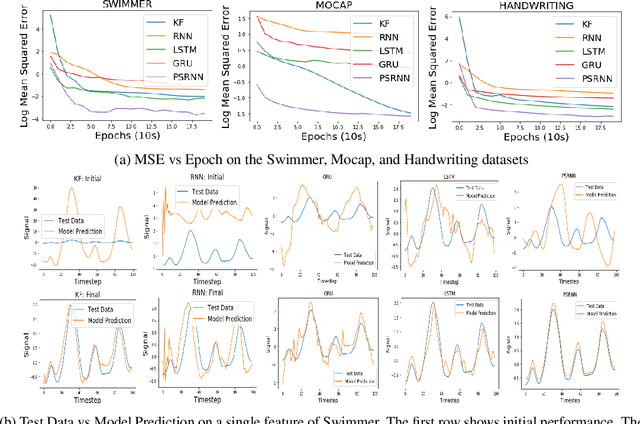
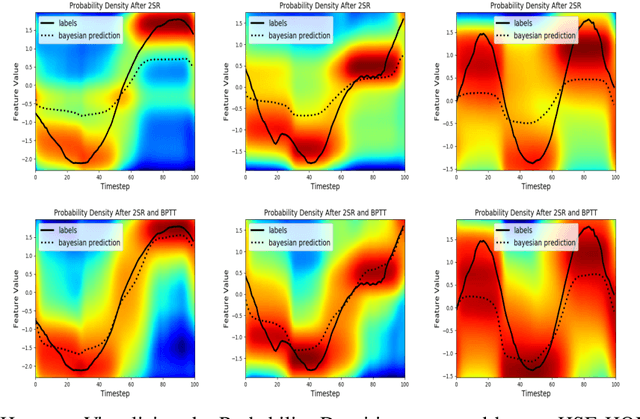
We present a new model, Predictive State Recurrent Neural Networks (PSRNNs), for filtering and prediction in dynamical systems. PSRNNs draw on insights from both Recurrent Neural Networks (RNNs) and Predictive State Representations (PSRs), and inherit advantages from both types of models. Like many successful RNN architectures, PSRNNs use (potentially deeply composed) bilinear transfer functions to combine information from multiple sources. We show that such bilinear functions arise naturally from state updates in Bayes filters like PSRs, in which observations can be viewed as gating belief states. We also show that PSRNNs can be learned effectively by combining Backpropogation Through Time (BPTT) with an initialization derived from a statistically consistent learning algorithm for PSRs called two-stage regression (2SR). Finally, we show that PSRNNs can be factorized using tensor decomposition, reducing model size and suggesting interesting connections to existing multiplicative architectures such as LSTMs. We applied PSRNNs to 4 datasets, and showed that we outperform several popular alternative approaches to modeling dynamical systems in all cases.

Practical Learning of Predictive State Representations

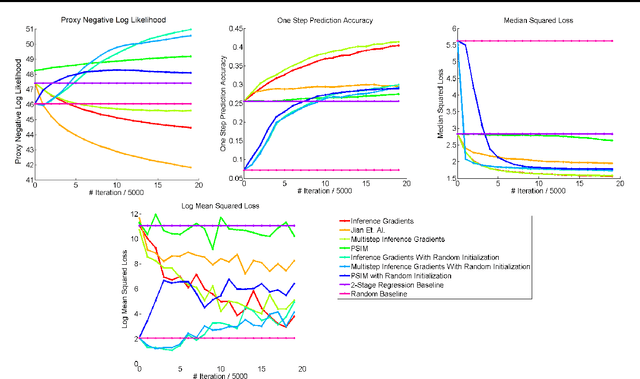
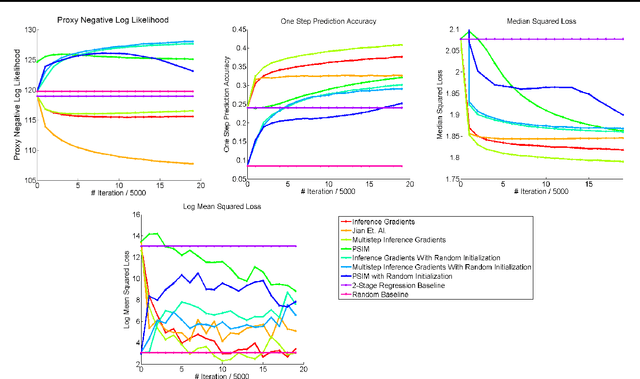
Over the past decade there has been considerable interest in spectral algorithms for learning Predictive State Representations (PSRs). Spectral algorithms have appealing theoretical guarantees; however, the resulting models do not always perform well on inference tasks in practice. One reason for this behavior is the mismatch between the intended task (accurate filtering or prediction) and the loss function being optimized by the algorithm (estimation error in model parameters). A natural idea is to improve performance by refining PSRs using an algorithm such as EM. Unfortunately it is not obvious how to apply apply an EM style algorithm in the context of PSRs as the Log Likelihood is not well defined for all PSRs. We show that it is possible to overcome this problem using ideas from Predictive State Inference Machines. We combine spectral algorithms for PSRs as a consistent and efficient initialization with PSIM-style updates to refine the resulting model parameters. By combining these two ideas we develop Inference Gradients, a simple, fast, and robust method for practical learning of PSRs. Inference Gradients performs gradient descent in the PSR parameter space to optimize an inference-based loss function like PSIM. Because Inference Gradients uses a spectral initialization we get the same consistency benefits as PSRs. We show that Inference Gradients outperforms both PSRs and PSIMs on real and synthetic data sets.

Supervised Learning for Dynamical System Learning

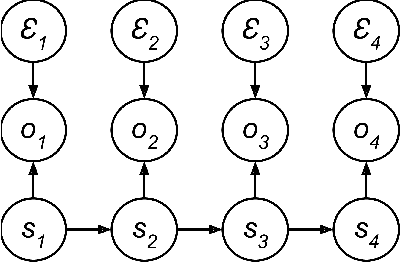
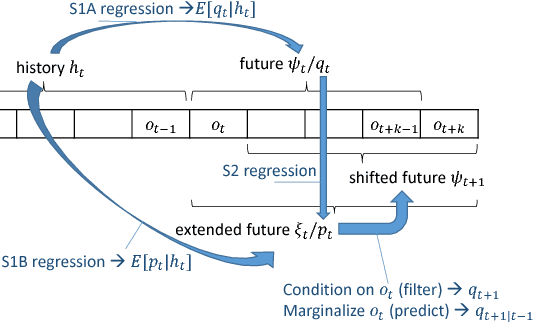
Recently there has been substantial interest in spectral methods for learning dynamical systems. These methods are popular since they often offer a good tradeoff between computational and statistical efficiency. Unfortunately, they can be difficult to use and extend in practice: e.g., they can make it difficult to incorporate prior information such as sparsity or structure. To address this problem, we present a new view of dynamical system learning: we show how to learn dynamical systems by solving a sequence of ordinary supervised learning problems, thereby allowing users to incorporate prior knowledge via standard techniques such as L1 regularization. Many existing spectral methods are special cases of this new framework, using linear regression as the supervised learner. We demonstrate the effectiveness of our framework by showing examples where nonlinear regression or lasso let us learn better state representations than plain linear regression does; the correctness of these instances follows directly from our general analysis.

Large-scale randomized-coordinate descent methods with non-separable linear constraints

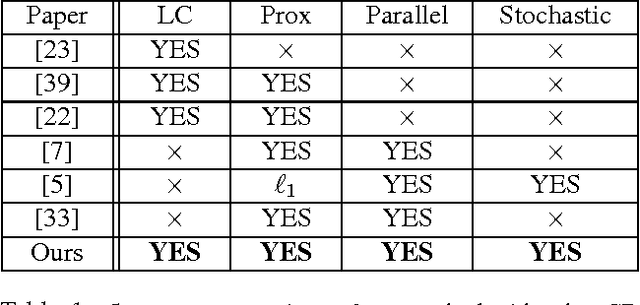
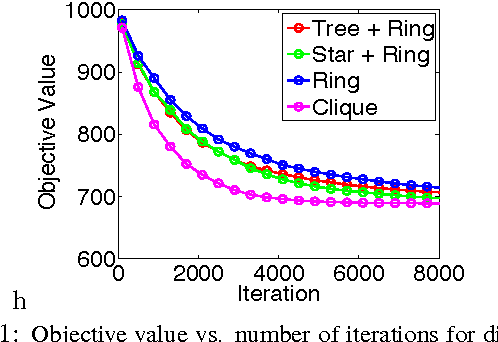
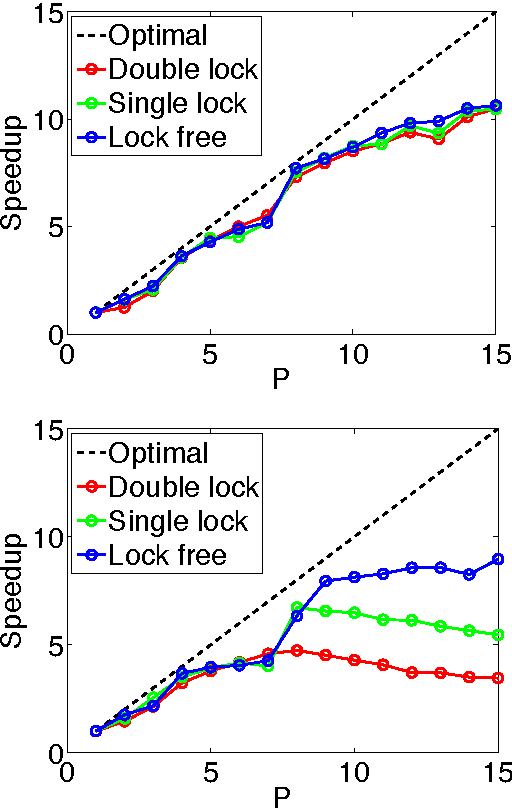
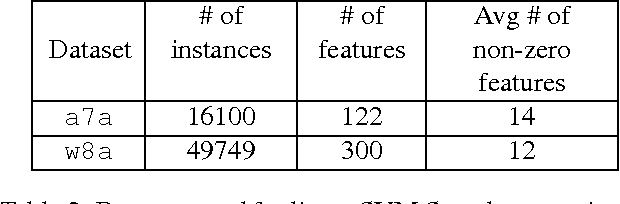
We develop randomized (block) coordinate descent (CD) methods for linearly constrained convex optimization. Unlike most CD methods, we do not assume the constraints to be separable, but let them be coupled linearly. To our knowledge, ours is the first CD method that allows linear coupling constraints, without making the global iteration complexity have an exponential dependence on the number of constraints. We present algorithms and analysis for four key problem scenarios: (i) smooth; (ii) smooth + nonsmooth separable; (iii) asynchronous parallel; and (iv) stochastic. We illustrate empirical behavior of our algorithms by simulation experiments.