An Efficient, Expressive and Local Minima-free Method for Learning Controlled Dynamical Systems
Paper and Code
Feb 28, 2018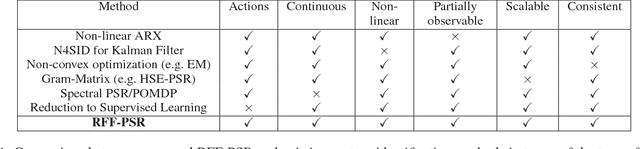
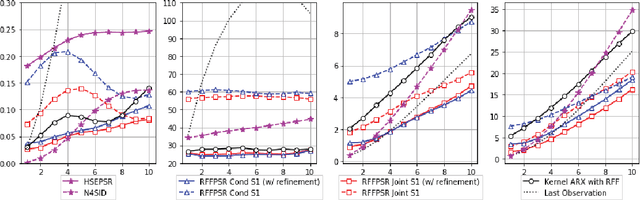

We propose a framework for modeling and estimating the state of controlled dynamical systems, where an agent can affect the system through actions and receives partial observations. Based on this framework, we propose the Predictive State Representation with Random Fourier Features (RFFPSR). A key property in RFF-PSRs is that the state estimate is represented by a conditional distribution of future observations given future actions. RFF-PSRs combine this representation with moment-matching, kernel embedding and local optimization to achieve a method that enjoys several favorable qualities: It can represent controlled environments which can be affected by actions; it has an efficient and theoretically justified learning algorithm; it uses a non-parametric representation that has expressive power to represent continuous non-linear dynamics. We provide a detailed formulation, a theoretical analysis and an experimental evaluation that demonstrates the effectiveness of our method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge