Identifying Driver Interactions via Conditional Behavior Prediction

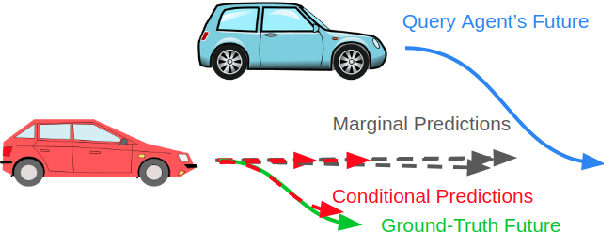
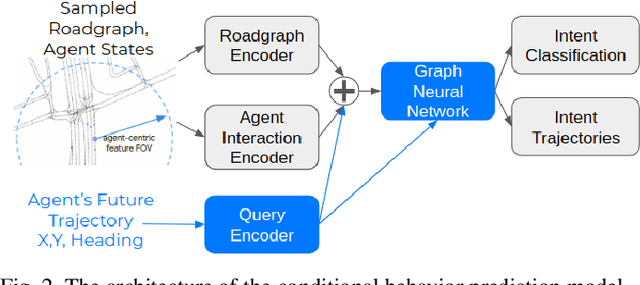
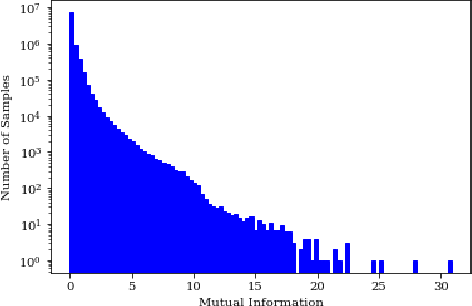
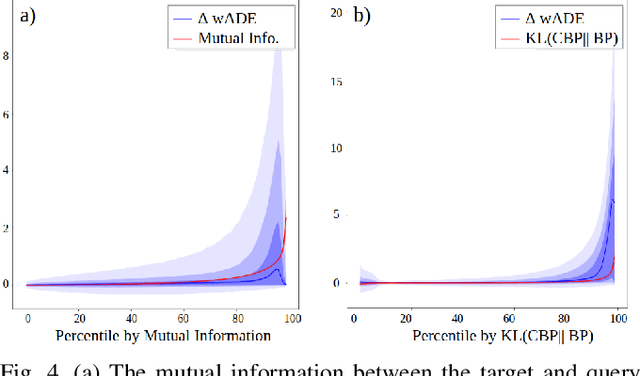
Interactive driving scenarios, such as lane changes, merges and unprotected turns, are some of the most challenging situations for autonomous driving. Planning in interactive scenarios requires accurately modeling the reactions of other agents to different future actions of the ego agent. We develop end-to-end models for conditional behavior prediction (CBP) that take as an input a query future trajectory for an ego-agent, and predict distributions over future trajectories for other agents conditioned on the query. Leveraging such a model, we develop a general-purpose agent interactivity score derived from probabilistic first principles. The interactivity score allows us to find interesting interactive scenarios for training and evaluating behavior prediction models. We further demonstrate that the proposed score is effective for agent prioritization under computational budget constraints.

Composable Learning with Sparse Kernel Representations

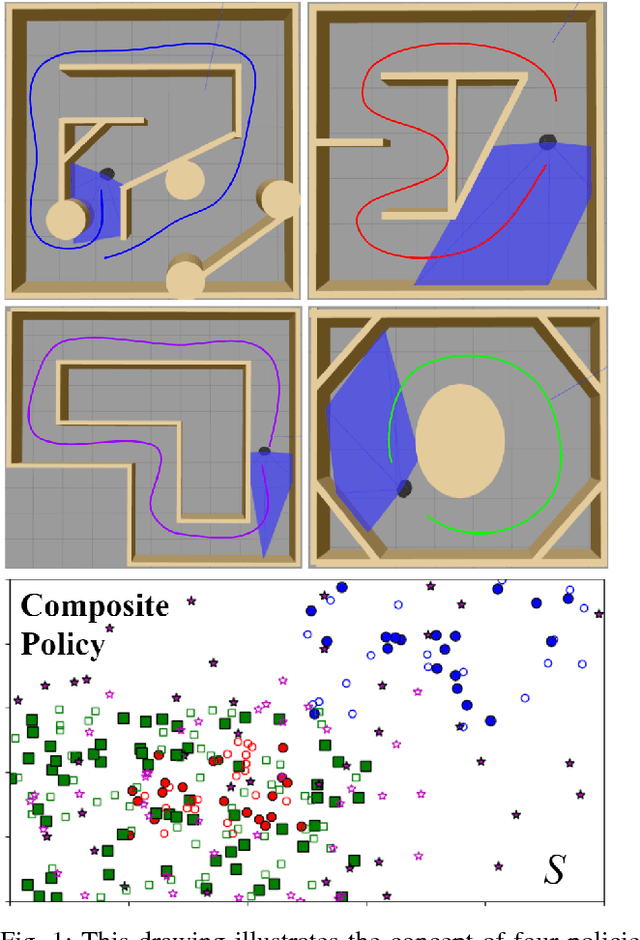
We present a reinforcement learning algorithm for learning sparse non-parametric controllers in a Reproducing Kernel Hilbert Space. We improve the sample complexity of this approach by imposing a structure of the state-action function through a normalized advantage function (NAF). This representation of the policy enables efficiently composing multiple learned models without additional training samples or interaction with the environment. We demonstrate the performance of this algorithm on learning obstacle-avoidance policies in multiple simulations of a robot equipped with a laser scanner while navigating in a 2D environment. We apply the composition operation to various policy combinations and test them to show that the composed policies retain the performance of their components. We also transfer the composed policy directly to a physical platform operating in an arena with obstacles in order to demonstrate a degree of generalization.

Learning Connectivity for Data Distribution in Robot Teams

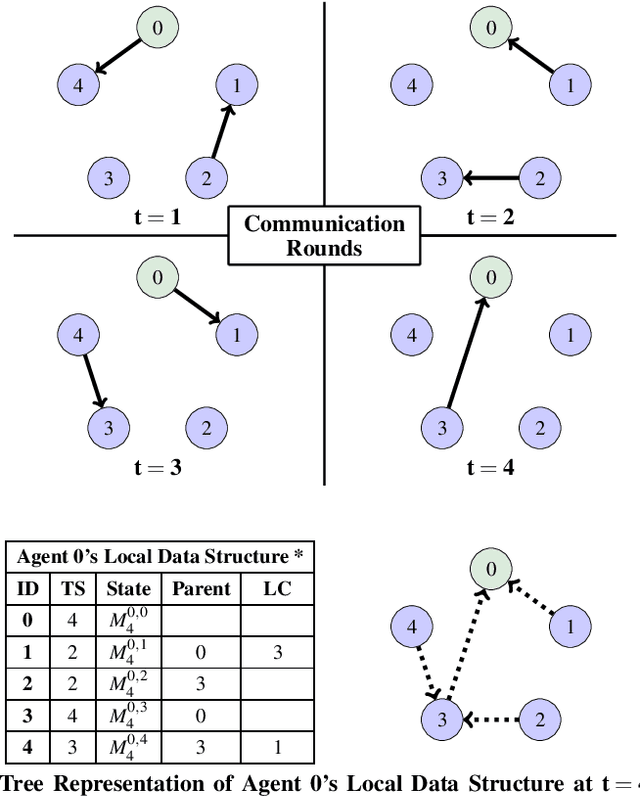
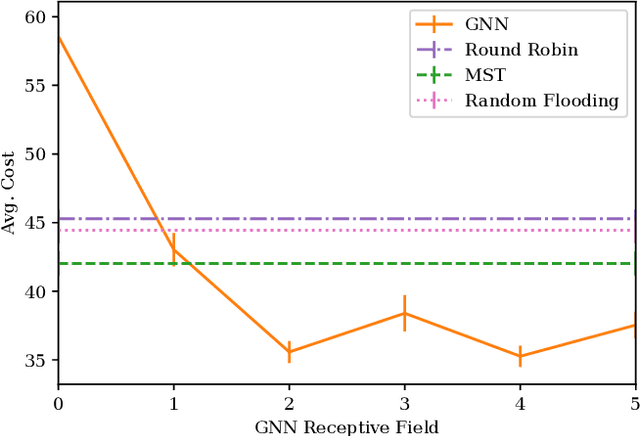
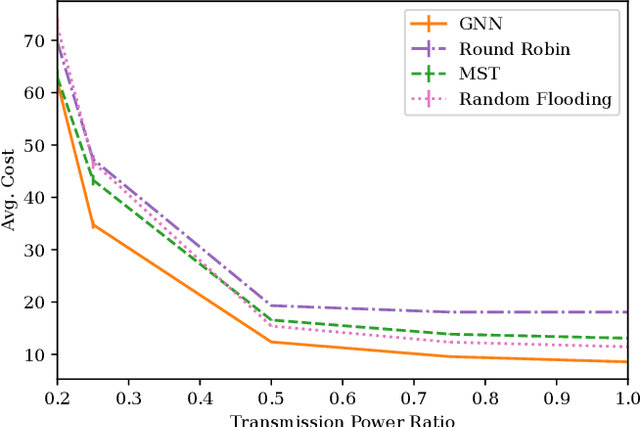
Many algorithms for control of multi-robot teams operate under the assumption that low-latency, global state information necessary to coordinate agent actions can readily be disseminated among the team. However, in harsh environments with no existing communication infrastructure, robots must form ad-hoc networks, forcing the team to operate in a distributed fashion. To overcome this challenge, we propose a task-agnostic, decentralized, low-latency method for data distribution in ad-hoc networks using Graph Neural Networks (GNN). Our approach enables multi-agent algorithms based on global state information to function by ensuring it is available at each robot. To do this, agents glean information about the topology of the network from packet transmissions and feed it to a GNN running locally which instructs the agent when and where to transmit the latest state information. We train the distributed GNN communication policies via reinforcement learning using the average Age of Information as the reward function and show that it improves training stability compared to task-specific reward functions. Our approach performs favorably compared to industry-standard methods for data distribution such as random flooding and round robin. We also show that the trained policies generalize to larger teams of both static and mobile agents.

Decentralized Control with Graph Neural Networks

Dynamical systems consisting of a set of autonomous agents face the challenge of having to accomplish a global task, relying only on local information. While centralized controllers are readily available, they face limitations in terms of scalability and implementation, as they do not respect the distributed information structure imposed by the network system of agents. Given the difficulties in finding optimal decentralized controllers, we propose a novel framework using graph neural networks (GNNs) to learn these controllers. GNNs are well-suited for the task since they are naturally distributed architectures and exhibit good scalability and transferability properties. The problems of flocking and multi-agent path planning are explored to illustrate the potential of GNNs in learning decentralized controllers.

Multi-Robot Coverage and Exploration using Spatial Graph Neural Networks

The multi-robot coverage problem is an essential building block for systems that perform tasks like inspection or search and rescue. We discretize the coverage problem to induce a spatial graph of locations and represent robots as nodes in the graph. Then, we train a Graph Neural Network controller that leverages the spatial equivariance of the task to imitate an expert open-loop routing solution. This approach generalizes well to much larger maps and larger teams that are intractable for the expert. In particular, the model generalizes effectively to a simulation of ten quadrotors and dozens of buildings. We also demonstrate the GNN controller can surpass planning-based approaches in an exploration task.

Graph Neural Networks for Decentralized Controllers

Dynamical systems comprised of autonomous agents arise in many relevant problems such as multi-agent robotics, smart grids, or smart cities. Controlling these systems is of paramount importance to guarantee a successful deployment. Optimal centralized controllers are readily available but face limitations in terms of scalability and practical implementation. Optimal decentralized controllers, on the other hand, are difficult to find. In this paper, we use graph neural networks (GNNs) to learn decentralized controllers from data. GNNs are well-suited for the task since they are naturally distributed architectures. Furthermore, they are equivariant and stable, leading to good scalability and transferability properties. The problem of flocking is explored to illustrate the power of GNNs in learning decentralized controllers.

Graph Policy Gradients for Large Scale Robot Control

In this paper, we consider the problem of learning policies to control a large number of homogeneous robots. To this end, we propose a new algorithm we call Graph Policy Gradients (GPG) that exploits the underlying graph symmetry among the robots. The curse of dimensionality one encounters when working with a large number of robots is mitigated by employing a graph convolutional neural (GCN) network to parametrize policies for the robots. The GCN reduces the dimensionality of the problem by learning filters that aggregate information among robots locally, similar to how a convolutional neural network is able to learn local features in an image. Through experiments on formation flying, we show that our proposed method is able to scale better than existing reinforcement methods that employ fully connected networks. More importantly, we show that by using our locally learned filters we are able to zero-shot transfer policies trained on just three robots to over hundred robots.

Learning Decentralized Controllers for Robot Swarms with Graph Neural Networks

We consider the problem of finding distributed controllers for large networks of mobile robots with interacting dynamics and sparsely available communications. Our approach is to learn local controllers which require only local information and local communications at test time by imitating the policy of centralized controllers using global information at training time. By extending aggregation graph neural networks to time varying signals and time varying network support, we learn a single common local controller which exploits information from distant teammates using only local communication interchanges. We apply this approach to a decentralized linear quadratic regulator problem and observe how faster communication rates and smaller network degree increase the value of multi-hop information. Separate experiments learning a decentralized flocking controller demonstrate performance on communication graphs that change as the robots move.

Inverse Optimal Planning for Air Traffic Control

We envision a system that concisely describes the rules of air traffic control, assists human operators and supports dense autonomous air traffic around commercial airports. We develop a method to learn the rules of air traffic control from real data as a cost function via maximum entropy inverse reinforcement learning. This cost function is used as a penalty for a search-based motion planning method that discretizes both the control and the state space. We illustrate the methodology by showing that our approach can learn to imitate the airport arrival routes and separation rules of dense commercial air traffic. The resulting trajectories are shown to be safe, feasible, and efficient.

Nonparametric Stochastic Compositional Gradient Descent for Q-Learning in Continuous Markov Decision Problems

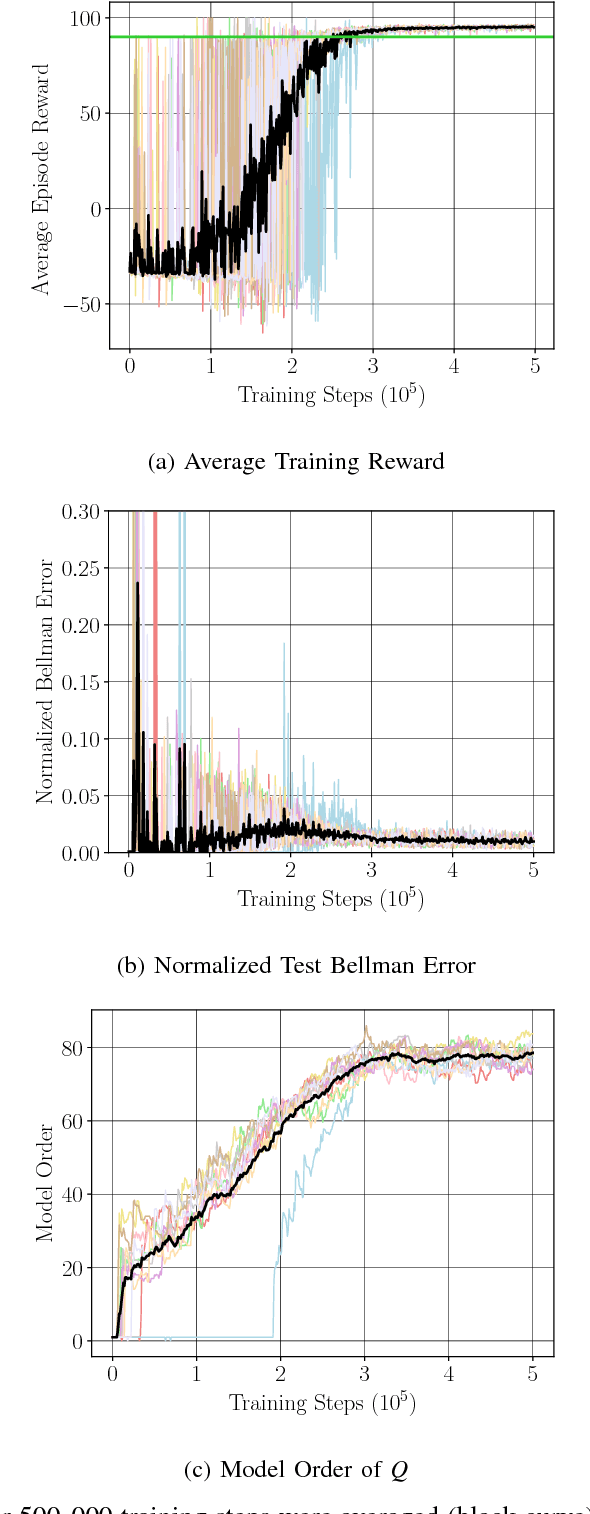
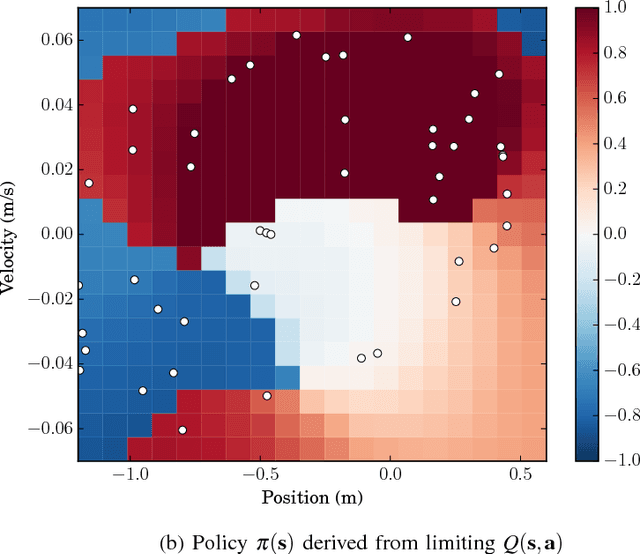
We consider Markov Decision Problems defined over continuous state and action spaces, where an autonomous agent seeks to learn a map from its states to actions so as to maximize its long-term discounted accumulation of rewards. We address this problem by considering Bellman's optimality equation defined over action-value functions, which we reformulate into a nested non-convex stochastic optimization problem defined over a Reproducing Kernel Hilbert Space (RKHS). We develop a functional generalization of stochastic quasi-gradient method to solve it, which, owing to the structure of the RKHS, admits a parameterization in terms of scalar weights and past state-action pairs which grows proportionately with the algorithm iteration index. To ameliorate this complexity explosion, we apply Kernel Orthogonal Matching Pursuit to the sequence of kernel weights and dictionaries, which yields a controllable error in the descent direction of the underlying optimization method. We prove that the resulting algorithm, called KQ-Learning, converges with probability 1 to a stationary point of this problem, yielding a fixed point of the Bellman optimality operator under the hypothesis that it belongs to the RKHS. Under constant learning rates, we further obtain convergence to a small Bellman error that depends on the chosen learning rates. Numerical evaluation on the Continuous Mountain Car and Inverted Pendulum tasks yields convergent parsimonious learned action-value functions, policies that are competitive with the state of the art, and exhibit reliable, reproducible learning behavior.