Nonparametric Stochastic Compositional Gradient Descent for Q-Learning in Continuous Markov Decision Problems
Paper and Code
Apr 19, 2018
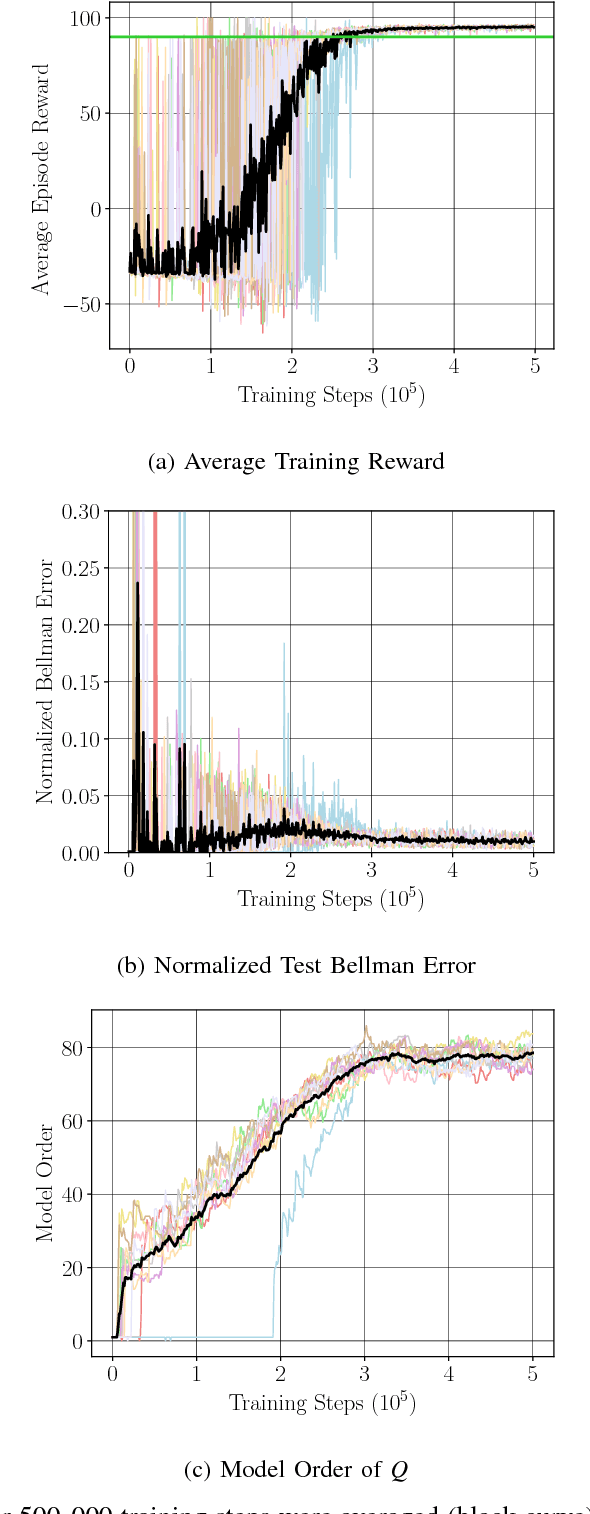
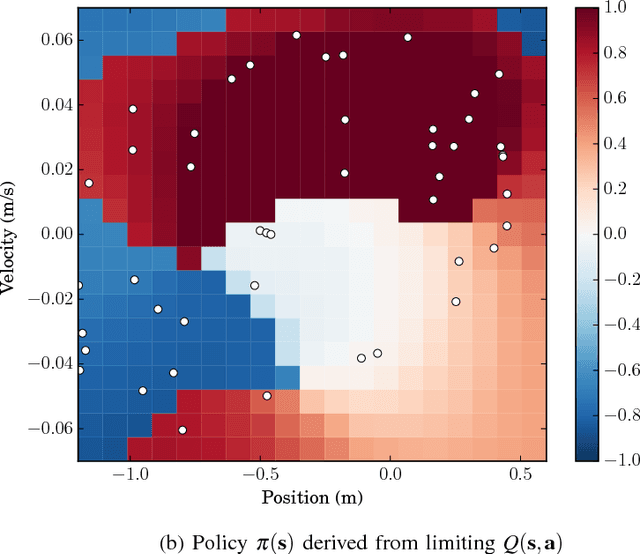

We consider Markov Decision Problems defined over continuous state and action spaces, where an autonomous agent seeks to learn a map from its states to actions so as to maximize its long-term discounted accumulation of rewards. We address this problem by considering Bellman's optimality equation defined over action-value functions, which we reformulate into a nested non-convex stochastic optimization problem defined over a Reproducing Kernel Hilbert Space (RKHS). We develop a functional generalization of stochastic quasi-gradient method to solve it, which, owing to the structure of the RKHS, admits a parameterization in terms of scalar weights and past state-action pairs which grows proportionately with the algorithm iteration index. To ameliorate this complexity explosion, we apply Kernel Orthogonal Matching Pursuit to the sequence of kernel weights and dictionaries, which yields a controllable error in the descent direction of the underlying optimization method. We prove that the resulting algorithm, called KQ-Learning, converges with probability 1 to a stationary point of this problem, yielding a fixed point of the Bellman optimality operator under the hypothesis that it belongs to the RKHS. Under constant learning rates, we further obtain convergence to a small Bellman error that depends on the chosen learning rates. Numerical evaluation on the Continuous Mountain Car and Inverted Pendulum tasks yields convergent parsimonious learned action-value functions, policies that are competitive with the state of the art, and exhibit reliable, reproducible learning behavior.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge