Unsupervised Learning of Sampling Distributions for Particle Filters

Accurate estimation of the states of a nonlinear dynamical system is crucial for their design, synthesis, and analysis. Particle filters are estimators constructed by simulating trajectories from a sampling distribution and averaging them based on their importance weight. For particle filters to be computationally tractable, it must be feasible to simulate the trajectories by drawing from the sampling distribution. Simultaneously, these trajectories need to reflect the reality of the nonlinear dynamical system so that the resulting estimators are accurate. Thus, the crux of particle filters lies in designing sampling distributions that are both easy to sample from and lead to accurate estimators. In this work, we propose to learn the sampling distributions. We put forward four methods for learning sampling distributions from observed measurements. Three of the methods are parametric methods in which we learn the mean and covariance matrix of a multivariate Gaussian distribution; each methods exploits a different aspect of the data (generic, time structure, graph structure). The fourth method is a nonparametric alternative in which we directly learn a transform of a uniform random variable. All four methods are trained in an unsupervised manner by maximizing the likelihood that the states may have produced the observed measurements. Our computational experiments demonstrate that learned sampling distributions exhibit better performance than designed, minimum-degeneracy sampling distributions.

Graph Filters for Signal Processing and Machine Learning on Graphs

Filters are fundamental in extracting information from data. For time series and image data that reside on Euclidean domains, filters are the crux of many signal processing and machine learning techniques, including convolutional neural networks. Increasingly, modern data also reside on networks and other irregular domains whose structure is better captured by a graph. To process and learn from such data, graph filters account for the structure of the underlying data domain. In this article, we provide a comprehensive overview of graph filters, including the different filtering categories, design strategies for each type, and trade-offs between different types of graph filters. We discuss how to extend graph filters into filter banks and graph neural networks to enhance the representational power; that is, to model a broader variety of signal classes, data patterns, and relationships. We also showcase the fundamental role of graph filters in signal processing and machine learning applications. Our aim is that this article serves the dual purpose of providing a unifying framework for both beginner and experienced researchers, as well as a common understanding that promotes collaborations between signal processing, machine learning, and application domains.

Unsupervised Optimal Power Flow Using Graph Neural Networks

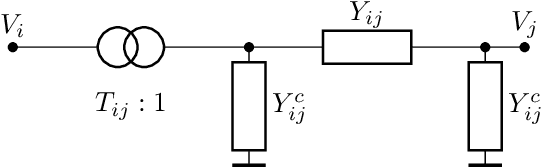
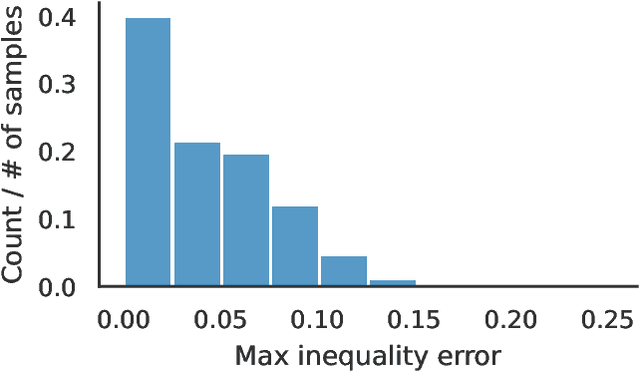
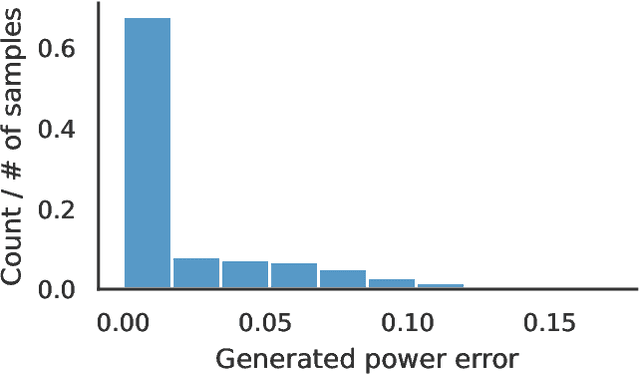
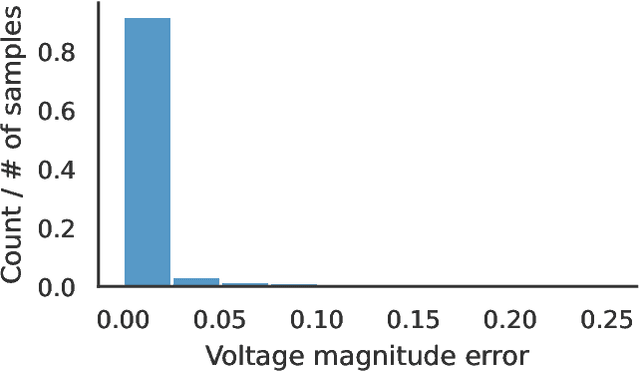
Optimal power flow (OPF) is a critical optimization problem that allocates power to the generators in order to satisfy the demand at a minimum cost. Solving this problem exactly is computationally infeasible in the general case. In this work, we propose to leverage graph signal processing and machine learning. More specifically, we use a graph neural network to learn a nonlinear parametrization between the power demanded and the corresponding allocation. We learn the solution in an unsupervised manner, minimizing the cost directly. In order to take into account the electrical constraints of the grid, we propose a novel barrier method that is differentiable and works on initially infeasible points. We show through simulations that the use of GNNs in this unsupervised learning context leads to solutions comparable to standard solvers while being computationally efficient and avoiding constraint violations most of the time.

Stability of Aggregation Graph Neural Networks

In this paper we study the stability properties of aggregation graph neural networks (Agg-GNNs) considering perturbations of the underlying graph. An Agg-GNN is a hybrid architecture where information is defined on the nodes of a graph, but it is processed block-wise by Euclidean CNNs on the nodes after several diffusions on the graph shift operator. We derive stability bounds for the mapping operator associated to a generic Agg-GNN, and we specify conditions under which such operators can be stable to deformations. We prove that the stability bounds are defined by the properties of the filters in the first layer of the CNN that acts on each node. Additionally, we show that there is a close relationship between the number of aggregations, the filter's selectivity, and the size of the stability constants. We also conclude that in Agg-GNNs the selectivity of the mapping operators is tied to the properties of the filters only in the first layer of the CNN stage. This shows a substantial difference with respect to the stability properties of selection GNNs, where the selectivity of the filters in all layers is constrained by their stability. We provide numerical evidence corroborating the results derived, testing the behavior of Agg-GNNs in real life application scenarios considering perturbations of different magnitude.

On Local Distributions in Graph Signal Processing

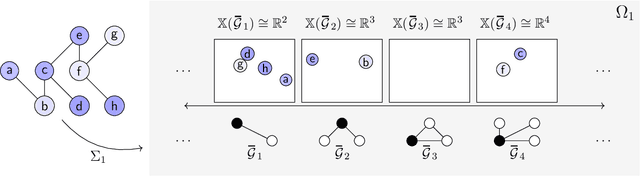
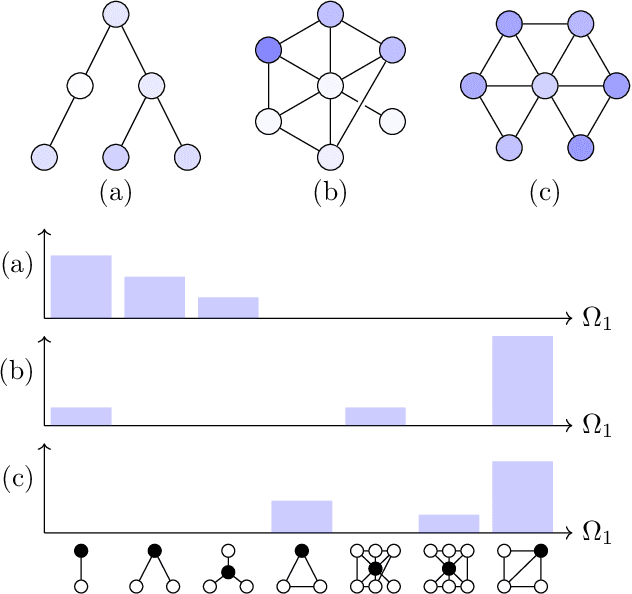
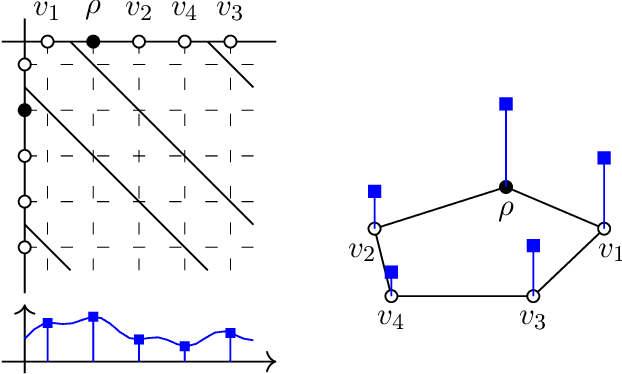
Graph filtering is the cornerstone operation in graph signal processing (GSP). Thus, understanding it is key in developing potent GSP methods. Graph filters are local and distributed linear operations, whose output depends only on the local neighborhood of each node. Moreover, a graph filter's output can be computed separately at each node by carrying out repeated exchanges with immediate neighbors. Graph filters can be compactly written as polynomials of a graph shift operator (typically, a sparse matrix description of the graph). This has led to relating the properties of the filters with the spectral properties of the corresponding matrix -- which encodes global structure of the graph. In this work, we propose a framework that relies solely on the local distribution of the neighborhoods of a graph. The crux of this approach is to describe graphs and graph signals in terms of a measurable space of rooted balls. Leveraging this, we are able to seamlessly compare graphs of different sizes and coming from different models, yielding results on the convergence of spectral densities, transferability of filters across arbitrary graphs, and continuity of graph signal properties with respect to the distribution of local substructures.

Stability Analysis of Unfolded WMMSE for Power Allocation

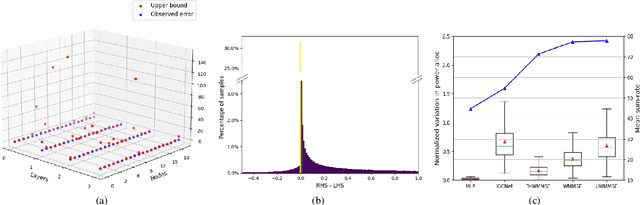
Power allocation is one of the fundamental problems in wireless networks and a wide variety of algorithms address this problem from different perspectives. A common element among these algorithms is that they rely on an estimation of the channel state, which may be inaccurate on account of hardware defects, noisy feedback systems, and environmental and adversarial disturbances. Therefore, it is essential that the output power allocation of these algorithms is stable with respect to input perturbations, to the extent that the variations in the output are bounded for bounded variations in the input. In this paper, we focus on UWMMSE -- a modern algorithm leveraging graph neural networks --, and illustrate its stability to additive input perturbations of bounded energy through both theoretical analysis and empirical validation.

Unrolling Particles: Unsupervised Learning of Sampling Distributions

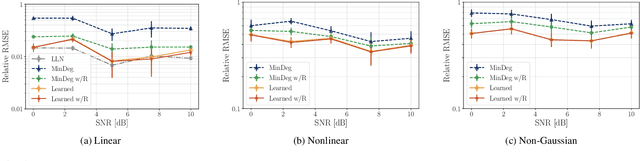
Particle filtering is used to compute good nonlinear estimates of complex systems. It samples trajectories from a chosen distribution and computes the estimate as a weighted average. Easy-to-sample distributions often lead to degenerate samples where only one trajectory carries all the weight, negatively affecting the resulting performance of the estimate. While much research has been done on the design of appropriate sampling distributions that would lead to controlled degeneracy, in this paper our objective is to \emph{learn} sampling distributions. Leveraging the framework of algorithm unrolling, we model the sampling distribution as a multivariate normal, and we use neural networks to learn both the mean and the covariance. We carry out unsupervised training of the model to minimize weight degeneracy, relying only on the observed measurements of the system. We show in simulations that the resulting particle filter yields good estimates in a wide range of scenarios.

A Robust Alternative for Graph Convolutional Neural Networks via Graph Neighborhood Filters

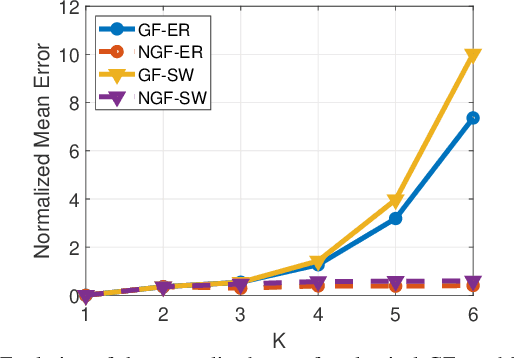
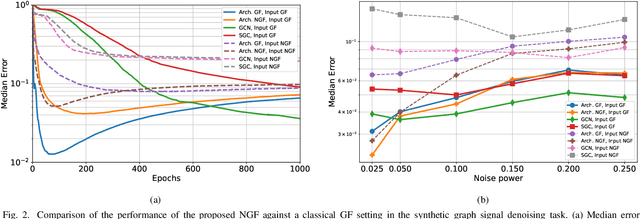
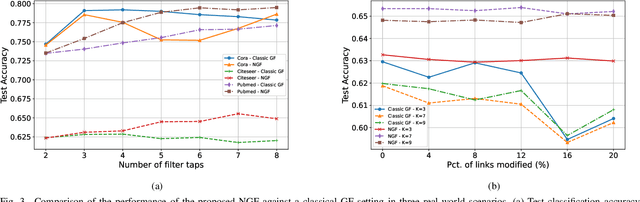
Graph convolutional neural networks (GCNNs) are popular deep learning architectures that, upon replacing regular convolutions with graph filters (GFs), generalize CNNs to irregular domains. However, classical GFs are prone to numerical errors since they consist of high-order polynomials. This problem is aggravated when several filters are applied in cascade, limiting the practical depth of GCNNs. To tackle this issue, we present the neighborhood graph filters (NGFs), a family of GFs that replaces the powers of the graph shift operator with $k$-hop neighborhood adjacency matrices. NGFs help to alleviate the numerical issues of traditional GFs, allow for the design of deeper GCNNs, and enhance the robustness to errors in the topology of the graph. To illustrate the advantage over traditional GFs in practical applications, we use NGFs in the design of deep neighborhood GCNNs to solve graph signal denoising and node classification problems over both synthetic and real-world data.

Wide and Deep Graph Neural Network with Distributed Online Learning

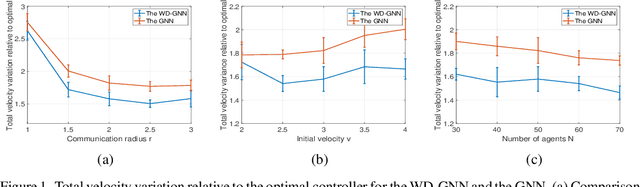
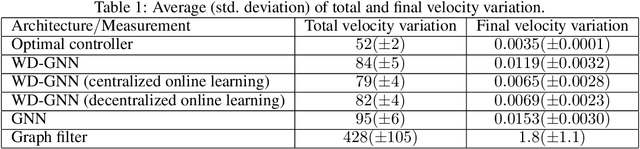
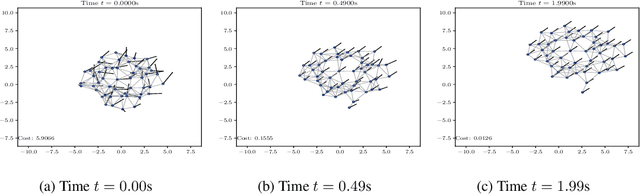
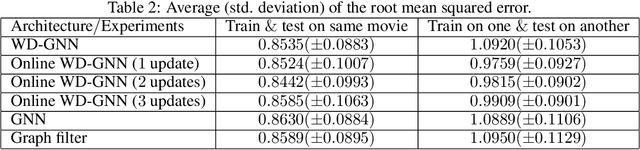
Graph neural networks (GNNs) are naturally distributed architectures for learning representations from network data. This renders them suitable candidates for decentralized tasks. In these scenarios, the underlying graph often changes with time due to link failures or topology variations, creating a mismatch between the graphs on which GNNs were trained and the ones on which they are tested. Online learning can be leveraged to retrain GNNs at testing time to overcome this issue. However, most online algorithms are centralized and usually offer guarantees only on convex problems, which GNNs rarely lead to. This paper develops the Wide and Deep GNN (WD-GNN), a novel architecture that can be updated with distributed online learning mechanisms. The WD-GNN consists of two components: the wide part is a linear graph filter and the deep part is a nonlinear GNN. At training time, the joint wide and deep architecture learns nonlinear representations from data. At testing time, the wide, linear part is retrained, while the deep, nonlinear one remains fixed. This often leads to a convex formulation. We further propose a distributed online learning algorithm that can be implemented in a decentralized setting. We also show the stability of the WD-GNN to changes of the underlying graph and analyze the convergence of the proposed online learning procedure. Experiments on movie recommendation, source localization and robot swarm control corroborate theoretical findings and show the potential of the WD-GNN for distributed online learning.

Scalable Perception-Action-Communication Loops with Convolutional and Graph Neural Networks

In this paper, we present a perception-action-communication loop design using Vision-based Graph Aggregation and Inference (VGAI). This multi-agent decentralized learning-to-control framework maps raw visual observations to agent actions, aided by local communication among neighboring agents. Our framework is implemented by a cascade of a convolutional and a graph neural network (CNN / GNN), addressing agent-level visual perception and feature learning, as well as swarm-level communication, local information aggregation and agent action inference, respectively. By jointly training the CNN and GNN, image features and communication messages are learned in conjunction to better address the specific task. We use imitation learning to train the VGAI controller in an offline phase, relying on a centralized expert controller. This results in a learned VGAI controller that can be deployed in a distributed manner for online execution. Additionally, the controller exhibits good scaling properties, with training in smaller teams and application in larger teams. Through a multi-agent flocking application, we demonstrate that VGAI yields performance comparable to or better than other decentralized controllers, using only the visual input modality and without accessing precise location or motion state information.