Convolutional Filtering with RKHS Algebras

In this paper, we develop a generalized theory of convolutional signal processing and neural networks for Reproducing Kernel Hilbert Spaces (RKHS). Leveraging the theory of algebraic signal processing (ASP), we show that any RKHS allows the formal definition of multiple algebraic convolutional models. We show that any RKHS induces algebras whose elements determine convolutional operators acting on RKHS elements. This approach allows us to achieve scalable filtering and learning as a byproduct of the convolutional model, and simultaneously take advantage of the well-known benefits of processing information in an RKHS. To emphasize the generality and usefulness of our approach, we show how algebraic RKHS can be used to define convolutional signal models on groups, graphons, and traditional Euclidean signal spaces. Furthermore, using algebraic RKHS models, we build convolutional networks, formally defining the notion of pointwise nonlinearities and deriving explicit expressions for the training. Such derivations are obtained in terms of the algebraic representation of the RKHS. We present a set of numerical experiments on real data in which wireless coverage is predicted from measurements captured by unmaned aerial vehicles. This particular real-life scenario emphasizes the benefits of the convolutional RKHS models in neural networks compared to fully connected and standard convolutional operators.

DiffKillR: Killing and Recreating Diffeomorphisms for Cell Annotation in Dense Microscopy Images

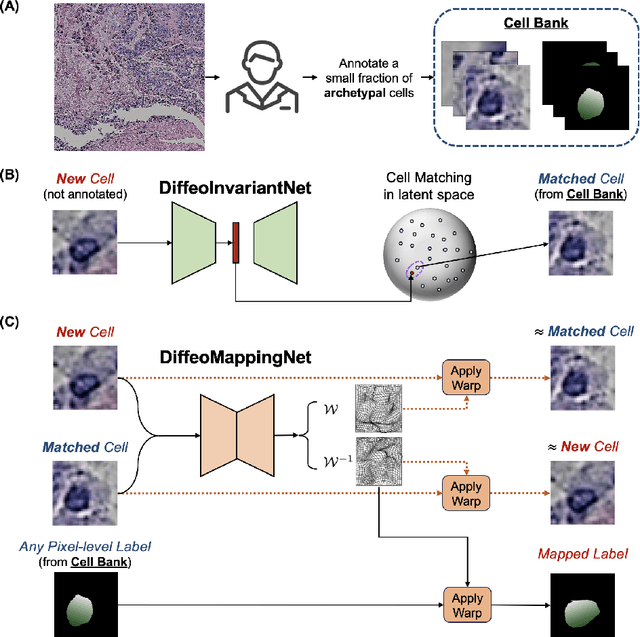
The proliferation of digital microscopy images, driven by advances in automated whole slide scanning, presents significant opportunities for biomedical research and clinical diagnostics. However, accurately annotating densely packed information in these images remains a major challenge. To address this, we introduce DiffKillR, a novel framework that reframes cell annotation as the combination of archetype matching and image registration tasks. DiffKillR employs two complementary neural networks: one that learns a diffeomorphism-invariant feature space for robust cell matching and another that computes the precise warping field between cells for annotation mapping. Using a small set of annotated archetypes, DiffKillR efficiently propagates annotations across large microscopy images, reducing the need for extensive manual labeling. More importantly, it is suitable for any type of pixel-level annotation. We will discuss the theoretical properties of DiffKillR and validate it on three microscopy tasks, demonstrating its advantages over existing supervised, semi-supervised, and unsupervised methods.

Sampling and Uniqueness Sets in Graphon Signal Processing

In this work, we study the properties of sampling sets on families of large graphs by leveraging the theory of graphons and graph limits. To this end, we extend to graphon signals the notion of removable and uniqueness sets, which was developed originally for the analysis of signals on graphs. We state the formal definition of a $\Lambda-$removable set and conditions under which a bandlimited graphon signal can be represented in a unique way when its samples are obtained from the complement of a given $\Lambda-$removable set in the graphon. By leveraging such results we show that graphon representations of graphs and graph signals can be used as a common framework to compare sampling sets between graphs with different numbers of nodes and edges, and different node labelings. Additionally, given a sequence of graphs that converges to a graphon, we show that the sequences of sampling sets whose graphon representation is identical in $[0,1]$ are convergent as well. We exploit the convergence results to provide an algorithm that obtains approximately close to optimal sampling sets. Performing a set of numerical experiments, we evaluate the quality of these sampling sets. Our results open the door for the efficient computation of optimal sampling sets in graphs of large size.

Non Commutative Convolutional Signal Models in Neural Networks: Stability to Small Deformations

In this paper we discuss the results recently published in~[1] about algebraic signal models (ASMs) based on non commutative algebras and their use in convolutional neural networks. Relying on the general tools from algebraic signal processing (ASP), we study the filtering and stability properties of non commutative convolutional filters. We show how non commutative filters can be stable to small perturbations on the space of operators. We also show that although the spectral components of the Fourier representation in a non commutative signal model are associated to spaces of dimension larger than one, there is a trade-off between stability and selectivity similar to that observed for commutative models. Our results have direct implications for group neural networks, multigraph neural networks and quaternion neural networks, among other non commutative architectures. We conclude by corroborating these results through numerical experiments.

Lie Group Algebra Convolutional Filters

In this paper we propose a framework to leverage Lie group symmetries on arbitrary spaces exploiting algebraic signal processing (ASP). We show that traditional group convolutions are one particular instantiation of a more general Lie group algebra homomorphism associated to an algebraic signal model rooted in the Lie group algebra $L^{1}(G)$ for given Lie group $G$. Exploiting this fact, we decouple the discretization of the Lie group convolution elucidating two separate sampling instances: the filter and the signal. To discretize the filters, we exploit the exponential map that links a Lie group with its associated Lie algebra. We show that the discrete Lie group filter learned from the data determines a unique filter in $L^{1}(G)$, and we show how this uniqueness of representation is defined by the bandwidth of the filter given a spectral representation. We also derive error bounds for the approximations of the filters in $L^{1}(G)$ with respect to its learned discrete representations. The proposed framework allows the processing of signals on spaces of arbitrary dimension and where the actions of some elements of the group are not necessarily well defined. Finally, we show that multigraph convolutional signal models come as the natural discrete realization of Lie group signal processing models, and we use this connection to establish stability results for Lie group algebra filters. To evaluate numerically our results, we build neural networks with these filters and we apply them in multiple datasets, including a knot classification problem.

Graphon Pooling for Reducing Dimensionality of Signals and Convolutional Operators on Graphs

In this paper we propose a pooling approach for convolutional information processing on graphs relying on the theory of graphons and limits of dense graph sequences. We present three methods that exploit the induced graphon representation of graphs and graph signals on partitions of [0, 1]2 in the graphon space. As a result we derive low dimensional representations of the convolutional operators, while a dimensionality reduction of the signals is achieved by simple local interpolation of functions in L2([0, 1]). We prove that those low dimensional representations constitute a convergent sequence of graphs and graph signals, respectively. The methods proposed and the theoretical guarantees that we provide show that the reduced graphs and signals inherit spectral-structural properties of the original quantities. We evaluate our approach with a set of numerical experiments performed on graph neural networks (GNNs) that rely on graphon pooling. We observe that graphon pooling performs significantly better than other approaches proposed in the literature when dimensionality reduction ratios between layers are large. We also observe that when graphon pooling is used we have, in general, less overfitting and lower computational cost.

Algebraic Convolutional Filters on Lie Group Algebras

Group convolutional neural networks are a useful tool for utilizing symmetries known to be in a signal; however, they require that the signal is defined on the group itself. Existing approaches either work directly with group signals, or they impose a lifting step with heuristics to compute the convolution which can be computationally costly. Taking an algebraic signal processing perspective, we propose a novel convolutional filter from the Lie group algebra directly, thereby removing the need to lift altogether. Furthermore, we establish stability of the filter by drawing connections to multigraph signal processing. The proposed filter is evaluated on a classification problem on two datasets with $SO(3)$ group symmetries.

Learning with Multigraph Convolutional Filters

In this paper, we introduce a convolutional architecture to perform learning when information is supported on multigraphs. Exploiting algebraic signal processing (ASP), we propose a convolutional signal processing model on multigraphs (MSP). Then, we introduce multigraph convolutional neural networks (MGNNs) as stacked and layered structures where information is processed according to an MSP model. We also develop a procedure for tractable computation of filter coefficients in the MGNN and a low cost method to reduce the dimensionality of the information transferred between layers. We conclude by comparing the performance of MGNNs against other learning architectures on an optimal resource allocation task for multi-channel communication systems.

Convolutional Learning on Multigraphs

Graph convolutional learning has led to many exciting discoveries in diverse areas. However, in some applications, traditional graphs are insufficient to capture the structure and intricacies of the data. In such scenarios, multigraphs arise naturally as discrete structures in which complex dynamics can be embedded. In this paper, we develop convolutional information processing on multigraphs and introduce convolutional multigraph neural networks (MGNNs). To capture the complex dynamics of information diffusion within and across each of the multigraph's classes of edges, we formalize a convolutional signal processing model, defining the notions of signals, filtering, and frequency representations on multigraphs. Leveraging this model, we develop a multigraph learning architecture, including a sampling procedure to reduce computational complexity. The introduced architecture is applied towards optimal wireless resource allocation and a hate speech localization task, offering improved performance over traditional graph neural networks.

Stability of Aggregation Graph Neural Networks

In this paper we study the stability properties of aggregation graph neural networks (Agg-GNNs) considering perturbations of the underlying graph. An Agg-GNN is a hybrid architecture where information is defined on the nodes of a graph, but it is processed block-wise by Euclidean CNNs on the nodes after several diffusions on the graph shift operator. We derive stability bounds for the mapping operator associated to a generic Agg-GNN, and we specify conditions under which such operators can be stable to deformations. We prove that the stability bounds are defined by the properties of the filters in the first layer of the CNN that acts on each node. Additionally, we show that there is a close relationship between the number of aggregations, the filter's selectivity, and the size of the stability constants. We also conclude that in Agg-GNNs the selectivity of the mapping operators is tied to the properties of the filters only in the first layer of the CNN stage. This shows a substantial difference with respect to the stability properties of selection GNNs, where the selectivity of the filters in all layers is constrained by their stability. We provide numerical evidence corroborating the results derived, testing the behavior of Agg-GNNs in real life application scenarios considering perturbations of different magnitude.