Landon Butler
An Odd Estimator for Shapley Values
Feb 01, 2026Abstract:The Shapley value is a ubiquitous framework for attribution in machine learning, encompassing feature importance, data valuation, and causal inference. However, its exact computation is generally intractable, necessitating efficient approximation methods. While the most effective and popular estimators leverage the paired sampling heuristic to reduce estimation error, the theoretical mechanism driving this improvement has remained opaque. In this work, we provide an elegant and fundamental justification for paired sampling: we prove that the Shapley value depends exclusively on the odd component of the set function, and that paired sampling orthogonalizes the regression objective to filter out the irrelevant even component. Leveraging this insight, we propose OddSHAP, a novel consistent estimator that performs polynomial regression solely on the odd subspace. By utilizing the Fourier basis to isolate this subspace and employing a proxy model to identify high-impact interactions, OddSHAP overcomes the combinatorial explosion of higher-order approximations. Through an extensive benchmark evaluation, we find that OddSHAP achieves state-of-the-art estimation accuracy.
ProxySPEX: Inference-Efficient Interpretability via Sparse Feature Interactions in LLMs
May 23, 2025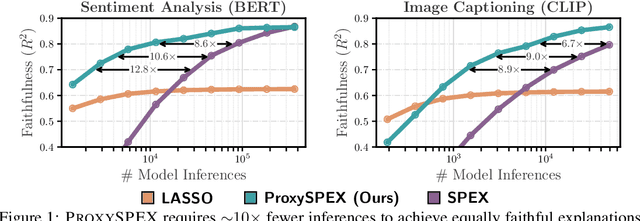

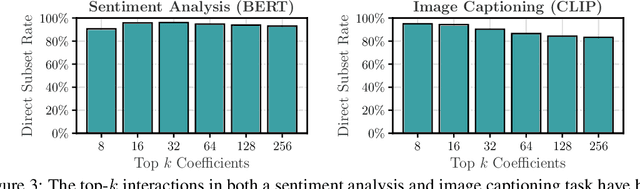
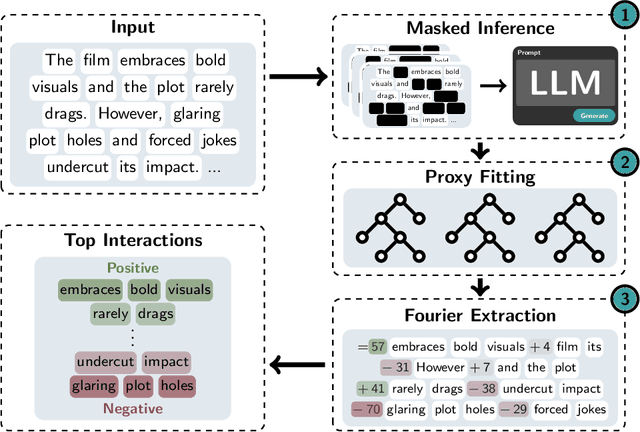
Abstract:Large Language Models (LLMs) have achieved remarkable performance by capturing complex interactions between input features. To identify these interactions, most existing approaches require enumerating all possible combinations of features up to a given order, causing them to scale poorly with the number of inputs $n$. Recently, Kang et al. (2025) proposed SPEX, an information-theoretic approach that uses interaction sparsity to scale to $n \approx 10^3$ features. SPEX greatly improves upon prior methods but requires tens of thousands of model inferences, which can be prohibitive for large models. In this paper, we observe that LLM feature interactions are often hierarchical -- higher-order interactions are accompanied by their lower-order subsets -- which enables more efficient discovery. To exploit this hierarchy, we propose ProxySPEX, an interaction attribution algorithm that first fits gradient boosted trees to masked LLM outputs and then extracts the important interactions. Experiments across four challenging high-dimensional datasets show that ProxySPEX more faithfully reconstructs LLM outputs by 20% over marginal attribution approaches while using $10\times$ fewer inferences than SPEX. By accounting for interactions, ProxySPEX identifies features that influence model output over 20% more than those selected by marginal approaches. Further, we apply ProxySPEX to two interpretability tasks. Data attribution, where we identify interactions among CIFAR-10 training samples that influence test predictions, and mechanistic interpretability, where we uncover interactions between attention heads, both within and across layers, on a question-answering task. ProxySPEX identifies interactions that enable more aggressive pruning of heads than marginal approaches.
SPEX: Scaling Feature Interaction Explanations for LLMs
Feb 19, 2025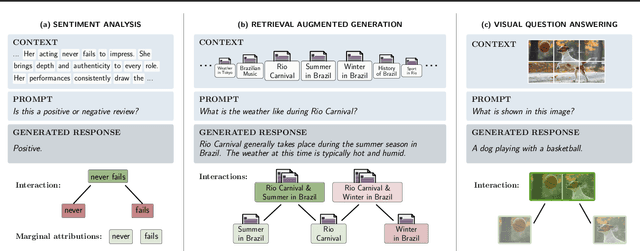

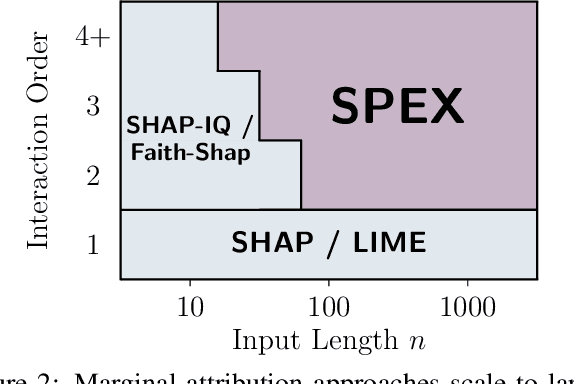
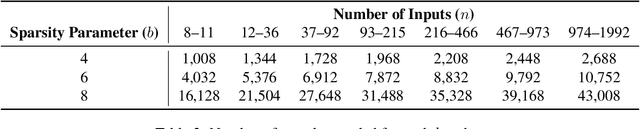
Abstract:Large language models (LLMs) have revolutionized machine learning due to their ability to capture complex interactions between input features. Popular post-hoc explanation methods like SHAP provide marginal feature attributions, while their extensions to interaction importances only scale to small input lengths ($\approx 20$). We propose Spectral Explainer (SPEX), a model-agnostic interaction attribution algorithm that efficiently scales to large input lengths ($\approx 1000)$. SPEX exploits underlying natural sparsity among interactions -- common in real-world data -- and applies a sparse Fourier transform using a channel decoding algorithm to efficiently identify important interactions. We perform experiments across three difficult long-context datasets that require LLMs to utilize interactions between inputs to complete the task. For large inputs, SPEX outperforms marginal attribution methods by up to 20% in terms of faithfully reconstructing LLM outputs. Further, SPEX successfully identifies key features and interactions that strongly influence model output. For one of our datasets, HotpotQA, SPEX provides interactions that align with human annotations. Finally, we use our model-agnostic approach to generate explanations to demonstrate abstract reasoning in closed-source LLMs (GPT-4o mini) and compositional reasoning in vision-language models.
Learning to Understand: Identifying Interactions via the Mobius Transform
Feb 04, 2024Abstract:One of the most fundamental problems in machine learning is finding interpretable representations of the functions we learn. The Mobius transform is a useful tool for this because its coefficients correspond to unique importance scores on sets of input variables. The Mobius Transform is strongly related (and in some cases equivalent) to the concept of Shapley value, which is a widely used game-theoretic notion of importance. This work focuses on the (typical) regime where the fraction of non-zero Mobius coefficients (and thus interactions between inputs) is small compared to the set of all $2^n$ possible interactions between $n$ inputs. When there are $K = O(2^{n \delta})$ with $\delta \leq \frac{1}{3}$ non-zero coefficients chosen uniformly at random, our algorithm exactly recovers the Mobius transform in $O(Kn)$ samples and $O(Kn^2)$ time with vanishing error as $K \rightarrow \infty$, the first non-adaptive algorithm to do so. We also uncover a surprising connection between group testing and the Mobius transform. In the case where all interactions are between at most $t = \Theta(n^{\alpha})$ inputs, for $\alpha < 0.409$, we are able to leverage results from group testing to provide the first algorithm that computes the Mobius transform in $O(Kt\log n)$ sample complexity and $O(K\mathrm{poly}(n))$ time with vanishing error as $K \rightarrow \infty$. Finally, we present a robust version of this algorithm that achieves the same sample and time complexity under some assumptions, but with a factor depending on noise variance. Our work is deeply interdisciplinary, drawing from tools spanning across signal processing, algebra, information theory, learning theory and group testing to address this important problem at the forefront of machine learning.
Non Commutative Convolutional Signal Models in Neural Networks: Stability to Small Deformations
Oct 05, 2023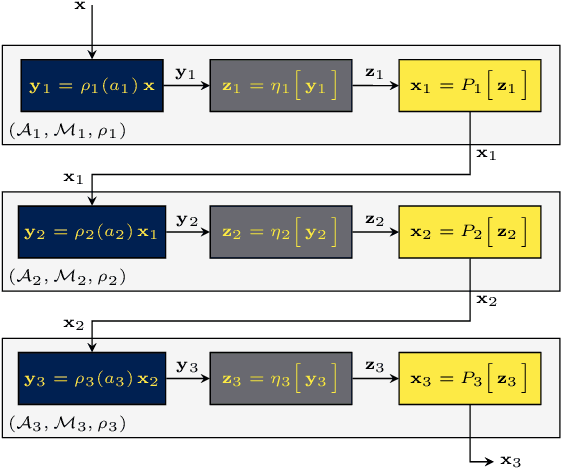
Abstract:In this paper we discuss the results recently published in~[1] about algebraic signal models (ASMs) based on non commutative algebras and their use in convolutional neural networks. Relying on the general tools from algebraic signal processing (ASP), we study the filtering and stability properties of non commutative convolutional filters. We show how non commutative filters can be stable to small perturbations on the space of operators. We also show that although the spectral components of the Fourier representation in a non commutative signal model are associated to spaces of dimension larger than one, there is a trade-off between stability and selectivity similar to that observed for commutative models. Our results have direct implications for group neural networks, multigraph neural networks and quaternion neural networks, among other non commutative architectures. We conclude by corroborating these results through numerical experiments.
Learning with Multigraph Convolutional Filters
Oct 28, 2022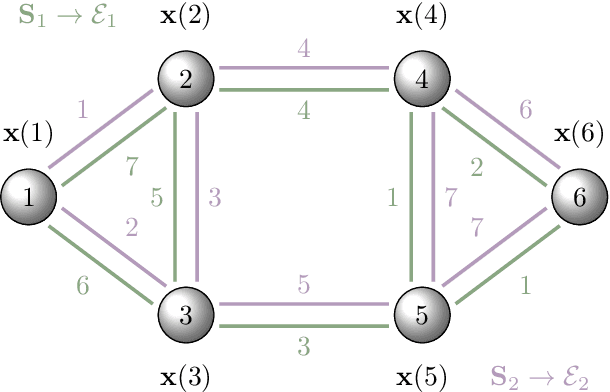


Abstract:In this paper, we introduce a convolutional architecture to perform learning when information is supported on multigraphs. Exploiting algebraic signal processing (ASP), we propose a convolutional signal processing model on multigraphs (MSP). Then, we introduce multigraph convolutional neural networks (MGNNs) as stacked and layered structures where information is processed according to an MSP model. We also develop a procedure for tractable computation of filter coefficients in the MGNN and a low cost method to reduce the dimensionality of the information transferred between layers. We conclude by comparing the performance of MGNNs against other learning architectures on an optimal resource allocation task for multi-channel communication systems.
Convolutional Learning on Multigraphs
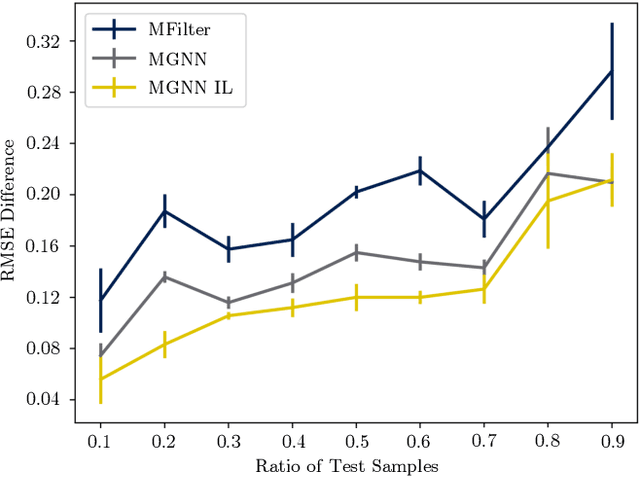
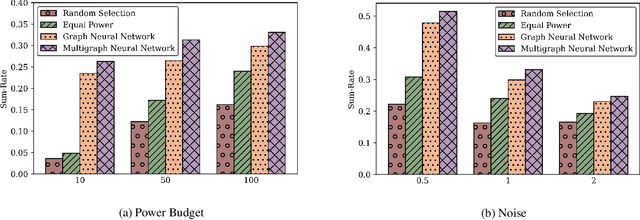
Sep 23, 2022Abstract:Graph convolutional learning has led to many exciting discoveries in diverse areas. However, in some applications, traditional graphs are insufficient to capture the structure and intricacies of the data. In such scenarios, multigraphs arise naturally as discrete structures in which complex dynamics can be embedded. In this paper, we develop convolutional information processing on multigraphs and introduce convolutional multigraph neural networks (MGNNs). To capture the complex dynamics of information diffusion within and across each of the multigraph's classes of edges, we formalize a convolutional signal processing model, defining the notions of signals, filtering, and frequency representations on multigraphs. Leveraging this model, we develop a multigraph learning architecture, including a sampling procedure to reduce computational complexity. The introduced architecture is applied towards optimal wireless resource allocation and a hate speech localization task, offering improved performance over traditional graph neural networks.
Learning Connectivity for Data Distribution in Robot Teams
Mar 08, 2021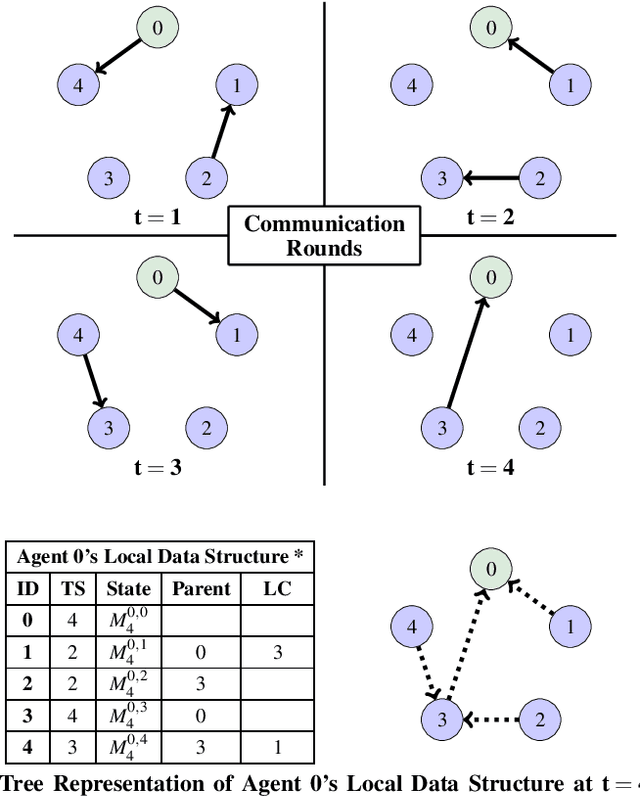

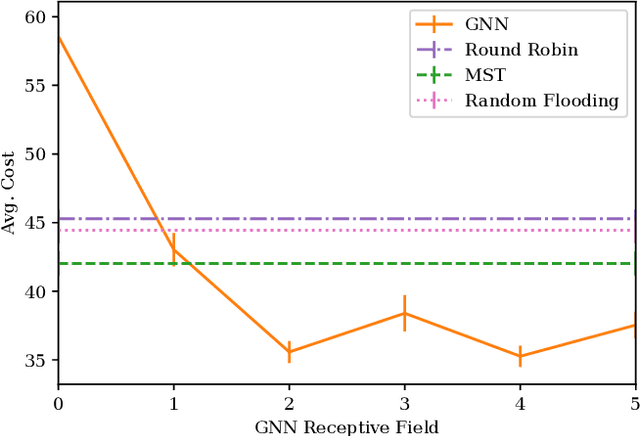
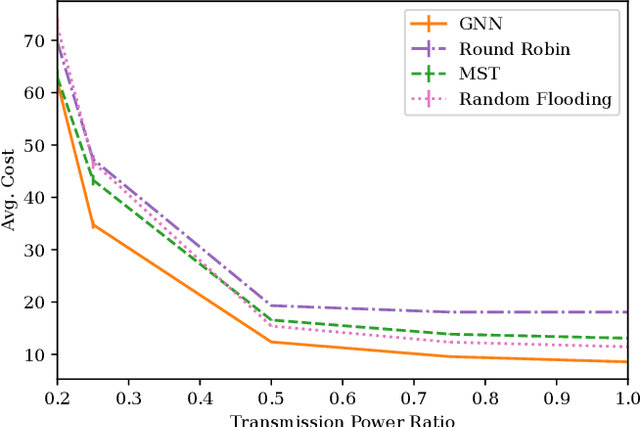
Abstract:Many algorithms for control of multi-robot teams operate under the assumption that low-latency, global state information necessary to coordinate agent actions can readily be disseminated among the team. However, in harsh environments with no existing communication infrastructure, robots must form ad-hoc networks, forcing the team to operate in a distributed fashion. To overcome this challenge, we propose a task-agnostic, decentralized, low-latency method for data distribution in ad-hoc networks using Graph Neural Networks (GNN). Our approach enables multi-agent algorithms based on global state information to function by ensuring it is available at each robot. To do this, agents glean information about the topology of the network from packet transmissions and feed it to a GNN running locally which instructs the agent when and where to transmit the latest state information. We train the distributed GNN communication policies via reinforcement learning using the average Age of Information as the reward function and show that it improves training stability compared to task-specific reward functions. Our approach performs favorably compared to industry-standard methods for data distribution such as random flooding and round robin. We also show that the trained policies generalize to larger teams of both static and mobile agents.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge