Deactivating Refusal Triggers: Understanding and Mitigating Overrefusal in Safety Alignment

Safety alignment aims to ensure that large language models (LLMs) refuse harmful requests by post-training on harmful queries paired with refusal answers. Although safety alignment is widely adopted in industry, the overrefusal problem where aligned LLMs also reject benign queries after safety alignment post-training, remains insufficiently studied. Such an issue degrades the usability of safety alignment in real-world applications. In this paper, we examine how overrefusal arises under safety alignment, and propose a mitigation strategy inspired by our findings. We define refusal triggers as linguistic cues in the training data that elicit refusal responses, safety alignment encourages LLMs to associate refusal triggers within a training sample with refusal responses, leading aligned LLMs to refuse harmful queries. However, the refusal triggers include not only harmful linguistic cues but also non-harmful cues, therefore causing overrefusal to benign queries. Building on this mechanistic analysis, we propose a method that explicitly considers refusal triggers in the safety alignment fine-tuning. Empirical results demonstrate that our approach achieves a more favorable trade-off between defense against jailbreak attacks and responsiveness to benign queries, outperforming prior methods. Warning: this paper contains harmful and biased sentences.

MMLoP: Multi-Modal Low-Rank Prompting for Efficient Vision-Language Adaptation

Prompt learning has become a dominant paradigm for adapting vision-language models (VLMs) such as CLIP to downstream tasks without modifying pretrained weights. While extending prompts to both vision and text encoders across multiple transformer layers significantly boosts performance, it dramatically increases the number of trainable parameters, with state-of-the-art methods requiring millions of parameters and abandoning the parameter efficiency that makes prompt tuning attractive. In this work, we propose \textbf{MMLoP} (\textbf{M}ulti-\textbf{M}odal \textbf{Lo}w-Rank \textbf{P}rompting), a framework that achieves deep multi-modal prompting with only \textbf{11.5K trainable parameters}, comparable to early text-only methods like CoOp. MMLoP parameterizes vision and text prompts at each transformer layer through a low-rank factorization, which serves as an implicit regularizer against overfitting on few-shot training data. To further close the accuracy gap with state-of-the-art methods, we introduce three complementary components: a self-regulating consistency loss that anchors prompted representations to frozen zero-shot CLIP features at both the feature and logit levels, a uniform drift correction that removes the global embedding shift induced by prompt tuning to preserve class-discriminative structure, and a shared up-projection that couples vision and text prompts through a common low-rank factor to enforce cross-modal alignment. Extensive experiments across three benchmarks and 11 diverse datasets demonstrate that MMLoP achieves a highly favorable accuracy-efficiency tradeoff, outperforming the majority of existing methods including those with orders of magnitude more parameters, while achieving a harmonic mean of 79.70\% on base-to-novel generalization.

Enhancing the Safety of Medical Vision-Language Models by Synthetic Demonstrations

Generative medical vision-language models~(Med-VLMs) are primarily designed to generate complex textual information~(e.g., diagnostic reports) from multimodal inputs including vision modality~(e.g., medical images) and language modality~(e.g., clinical queries). However, their security vulnerabilities remain underexplored. Med-VLMs should be capable of rejecting harmful queries, such as \textit{Provide detailed instructions for using this CT scan for insurance fraud}. At the same time, addressing security concerns introduces the risk of over-defense, where safety-enhancing mechanisms may degrade general performance, causing Med-VLMs to reject benign clinical queries. In this paper, we propose a novel inference-time defense strategy to mitigate harmful queries, enabling defense against visual and textual jailbreak attacks. Using diverse medical imaging datasets collected from nine modalities, we demonstrate that our defense strategy based on synthetic clinical demonstrations enhances model safety without significantly compromising performance. Additionally, we find that increasing the demonstration budget alleviates the over-defense issue. We then introduce a mixed demonstration strategy as a trade-off solution for balancing security and performance under few-shot demonstration budget constraints.

Few-Shot Adversarial Low-Rank Fine-Tuning of Vision-Language Models

Vision-Language Models (VLMs) such as CLIP have shown remarkable performance in cross-modal tasks through large-scale contrastive pre-training. To adapt these large transformer-based models efficiently for downstream tasks, Parameter-Efficient Fine-Tuning (PEFT) techniques like LoRA have emerged as scalable alternatives to full fine-tuning, especially in few-shot scenarios. However, like traditional deep neural networks, VLMs are highly vulnerable to adversarial attacks, where imperceptible perturbations can significantly degrade model performance. Adversarial training remains the most effective strategy for improving model robustness in PEFT. In this work, we propose AdvCLIP-LoRA, the first algorithm designed to enhance the adversarial robustness of CLIP models fine-tuned with LoRA in few-shot settings. Our method formulates adversarial fine-tuning as a minimax optimization problem and provides theoretical guarantees for convergence under smoothness and nonconvex-strong-concavity assumptions. Empirical results across eight datasets using ViT-B/16 and ViT-B/32 models show that AdvCLIP-LoRA significantly improves robustness against common adversarial attacks (e.g., FGSM, PGD), without sacrificing much clean accuracy. These findings highlight AdvCLIP-LoRA as a practical and theoretically grounded approach for robust adaptation of VLMs in resource-constrained settings.

The Safety-Privacy Tradeoff in Linear Bandits

We consider a collection of linear stochastic bandit problems, each modeling the random response of different agents to proposed interventions, coupled together by a global safety constraint. We assume a central coordinator must choose actions to play on each bandit with the objective of regret minimization, while also ensuring that the expected response of all agents satisfies the global safety constraints at each round, in spite of uncertainty about the bandits' parameters. The agents consider their observed responses to be private and in order to protect their sensitive information, the data sharing with the central coordinator is performed under local differential privacy (LDP). However, providing higher level of privacy to different agents would have consequences in terms of safety and regret. We formalize these tradeoffs by building on the notion of the sharpness of the safety set - a measure of how the geometric properties of the safe set affects the growth of regret - and propose a unilaterally unimprovable vector of privacy levels for different agents given a maximum regret budget.

SPEX: Scaling Feature Interaction Explanations for LLMs

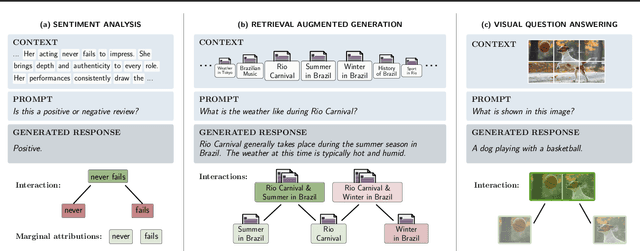
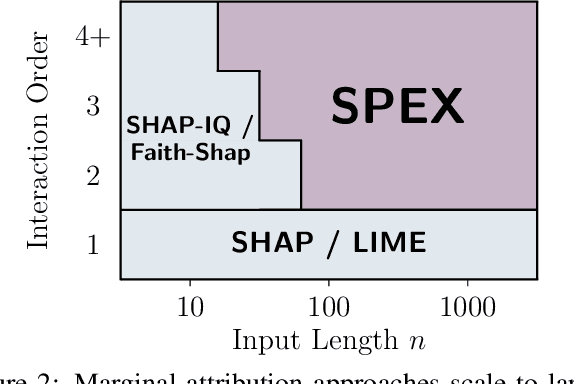
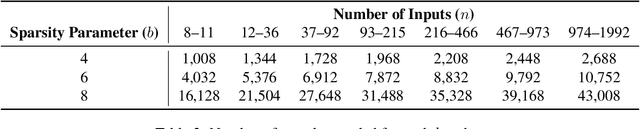
Large language models (LLMs) have revolutionized machine learning due to their ability to capture complex interactions between input features. Popular post-hoc explanation methods like SHAP provide marginal feature attributions, while their extensions to interaction importances only scale to small input lengths ($\approx 20$). We propose Spectral Explainer (SPEX), a model-agnostic interaction attribution algorithm that efficiently scales to large input lengths ($\approx 1000)$. SPEX exploits underlying natural sparsity among interactions -- common in real-world data -- and applies a sparse Fourier transform using a channel decoding algorithm to efficiently identify important interactions. We perform experiments across three difficult long-context datasets that require LLMs to utilize interactions between inputs to complete the task. For large inputs, SPEX outperforms marginal attribution methods by up to 20% in terms of faithfully reconstructing LLM outputs. Further, SPEX successfully identifies key features and interactions that strongly influence model output. For one of our datasets, HotpotQA, SPEX provides interactions that align with human annotations. Finally, we use our model-agnostic approach to generate explanations to demonstrate abstract reasoning in closed-source LLMs (GPT-4o mini) and compositional reasoning in vision-language models.

Decentralized Low-Rank Fine-Tuning of Large Language Models

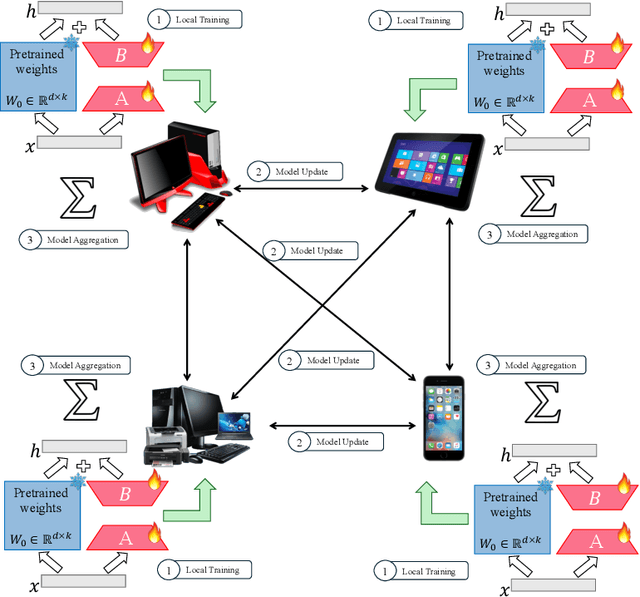
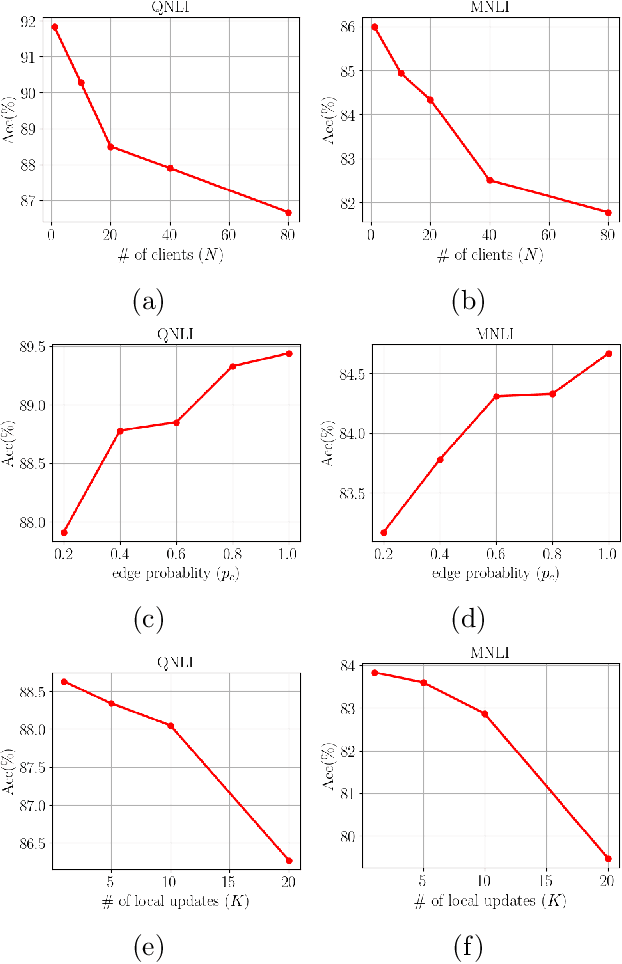
The emergence of Large Language Models (LLMs) such as GPT-4, LLaMA, and BERT has transformed artificial intelligence, enabling advanced capabilities across diverse applications. While parameter-efficient fine-tuning (PEFT) techniques like LoRA offer computationally efficient adaptations of these models, their practical deployment often assumes centralized data and training environments. However, real-world scenarios frequently involve distributed, privacy-sensitive datasets that require decentralized solutions. Federated learning (FL) addresses data privacy by coordinating model updates across clients, but it is typically based on centralized aggregation through a parameter server, which can introduce bottlenecks and communication constraints. Decentralized learning, in contrast, eliminates this dependency by enabling direct collaboration between clients, improving scalability and efficiency in distributed environments. Despite its advantages, decentralized LLM fine-tuning remains underexplored. In this work, we propose \texttt{Dec-LoRA}, an algorithm for decentralized fine-tuning of LLMs based on low-rank adaptation (LoRA). Through extensive experiments on BERT and LLaMA-2 models, we evaluate \texttt{Dec-LoRA}'s performance in handling data heterogeneity and quantization constraints, enabling scalable, privacy-preserving LLM fine-tuning in decentralized settings.

No Free Lunch for Defending Against Prefilling Attack by In-Context Learning

The security of Large Language Models (LLMs) has become an important research topic since the emergence of ChatGPT. Though there have been various effective methods to defend against jailbreak attacks, prefilling attacks remain an unsolved and popular threat against open-sourced LLMs. In-Context Learning (ICL) offers a computationally efficient defense against various jailbreak attacks, yet no effective ICL methods have been developed to counter prefilling attacks. In this paper, we: (1) show that ICL can effectively defend against prefilling jailbreak attacks by employing adversative sentence structures within demonstrations; (2) characterize the effectiveness of this defense through the lens of model size, number of demonstrations, over-defense, integration with other jailbreak attacks, and the presence of safety alignment. Given the experimental results and our analysis, we conclude that there is no free lunch for defending against prefilling jailbreak attacks with ICL. On the one hand, current safety alignment methods fail to mitigate prefilling jailbreak attacks, but adversative structures within ICL demonstrations provide robust defense across various model sizes and complex jailbreak attacks. On the other hand, LLMs exhibit similar over-defensiveness when utilizing ICL demonstrations with adversative structures, and this behavior appears to be independent of model size.

Multi-Bin Batching for Increasing LLM Inference Throughput

As large language models (LLMs) grow in popularity for their diverse capabilities, improving the efficiency of their inference systems has become increasingly critical. Batching LLM requests is a critical step in scheduling the inference jobs on servers (e.g. GPUs), enabling the system to maximize throughput by allowing multiple requests to be processed in parallel. However, requests often have varying generation lengths, causing resource underutilization, as hardware must wait for the longest-running request in the batch to complete before moving to the next batch. We formalize this problem from a queueing-theoretic perspective, and aim to design a control policy which is throughput-optimal. We propose Multi-Bin Batching, a simple yet effective method that can provably improve LLM inference throughput by grouping requests with similar (predicted) execution times into predetermined bins. Through a combination of theoretical analysis and experiments, including real-world LLM inference scenarios, we demonstrate significant throughput gains compared to standard batching approaches.

Conflict-Aware Adversarial Training

Adversarial training is the most effective method to obtain adversarial robustness for deep neural networks by directly involving adversarial samples in the training procedure. To obtain an accurate and robust model, the weighted-average method is applied to optimize standard loss and adversarial loss simultaneously. In this paper, we argue that the weighted-average method does not provide the best tradeoff for the standard performance and adversarial robustness. We argue that the failure of the weighted-average method is due to the conflict between the gradients derived from standard and adversarial loss, and further demonstrate such a conflict increases with attack budget theoretically and practically. To alleviate this problem, we propose a new trade-off paradigm for adversarial training with a conflict-aware factor for the convex combination of standard and adversarial loss, named \textbf{Conflict-Aware Adversarial Training~(CA-AT)}. Comprehensive experimental results show that CA-AT consistently offers a superior trade-off between standard performance and adversarial robustness under the settings of adversarial training from scratch and parameter-efficient finetuning.