Long-Term Fairness in Sequential Multi-Agent Selection with Positive Reinforcement

While much of the rapidly growing literature on fair decision-making focuses on metrics for one-shot decisions, recent work has raised the intriguing possibility of designing sequential decision-making to positively impact long-term social fairness. In selection processes such as college admissions or hiring, biasing slightly towards applicants from under-represented groups is hypothesized to provide positive feedback that increases the pool of under-represented applicants in future selection rounds, thus enhancing fairness in the long term. In this paper, we examine this hypothesis and its consequences in a setting in which multiple agents are selecting from a common pool of applicants. We propose the Multi-agent Fair-Greedy policy, that balances greedy score maximization and fairness. Under this policy, we prove that the resource pool and the admissions converge to a long-term fairness target set by the agents when the score distributions across the groups in the population are identical. We provide empirical evidence of existence of equilibria under non-identical score distributions through synthetic and adapted real-world datasets. We then sound a cautionary note for more complex applicant pool evolution models, under which uncoordinated behavior by the agents can cause negative reinforcement, leading to a reduction in the fraction of under-represented applicants. Our results indicate that, while positive reinforcement is a promising mechanism for long-term fairness, policies must be designed carefully to be robust to variations in the evolution model, with a number of open issues that remain to be explored by algorithm designers, social scientists, and policymakers.

Improving Robustness via Tilted Exponential Layer: A Communication-Theoretic Perspective

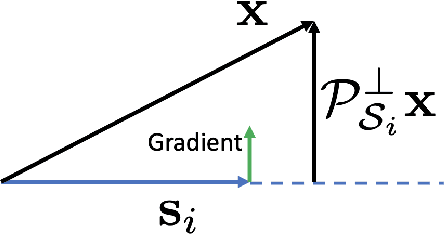
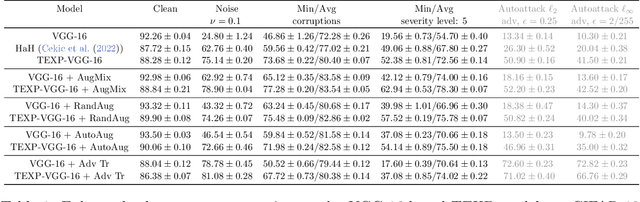
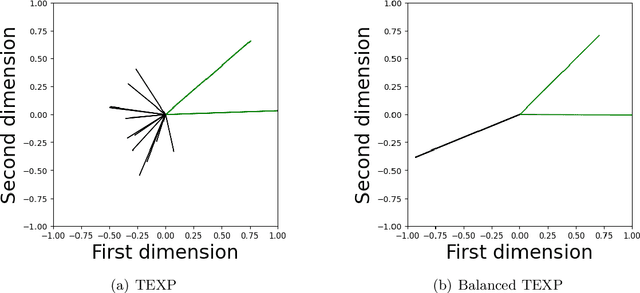
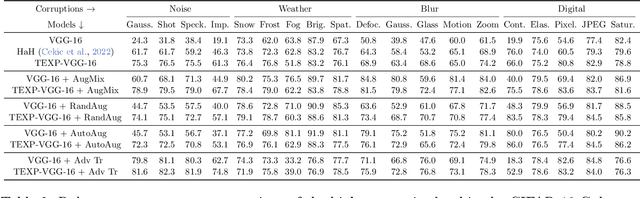
State-of-the-art techniques for enhancing robustness of deep networks mostly rely on empirical risk minimization with suitable data augmentation. In this paper, we propose a complementary approach motivated by communication theory, aimed at enhancing the signal-to-noise ratio at the output of a neural network layer via neural competition during learning and inference. In addition to minimization of a standard end-to-end cost, neurons compete to sparsely represent layer inputs by maximization of a tilted exponential (TEXP) objective function for the layer. TEXP learning can be interpreted as maximum likelihood estimation of matched filters under a Gaussian model for data noise. Inference in a TEXP layer is accomplished by replacing batch norm by a tilted softmax, which can be interpreted as computation of posterior probabilities for the competing signaling hypotheses represented by each neuron. After providing insights via simplified models, we show, by experimentation on standard image datasets, that TEXP learning and inference enhances robustness against noise and other common corruptions, without requiring data augmentation. Further cumulative gains in robustness against this array of distortions can be obtained by appropriately combining TEXP with data augmentation techniques.

Generalized Likelihood Ratio Test for Adversarially Robust Hypothesis Testing

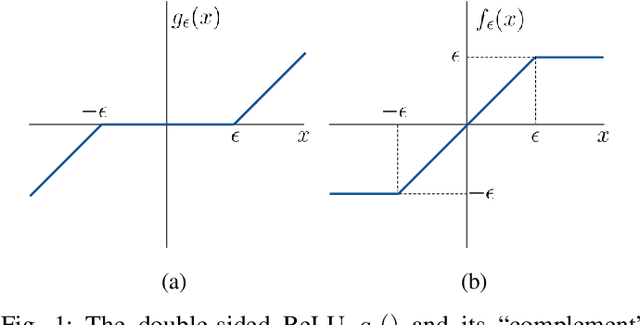
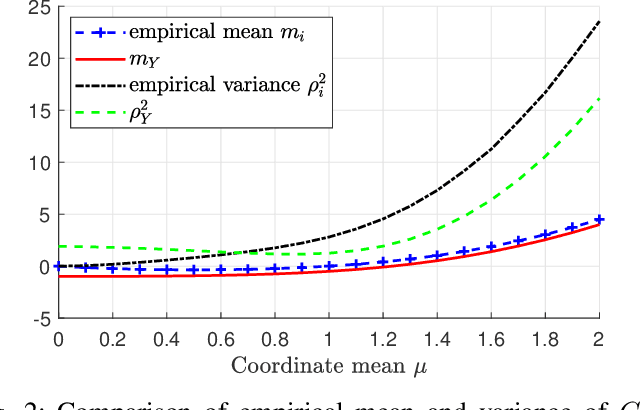
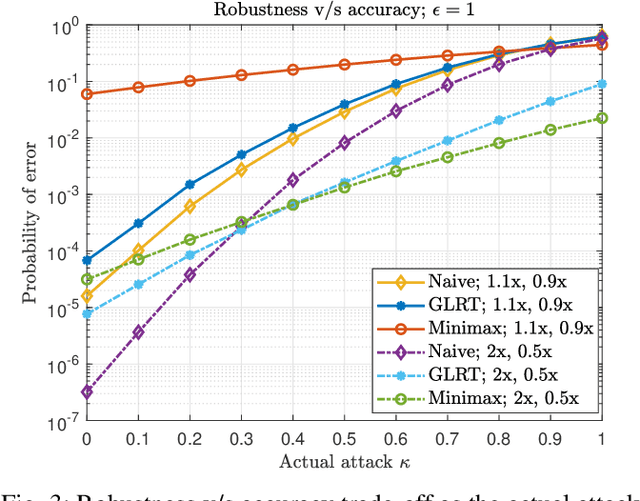
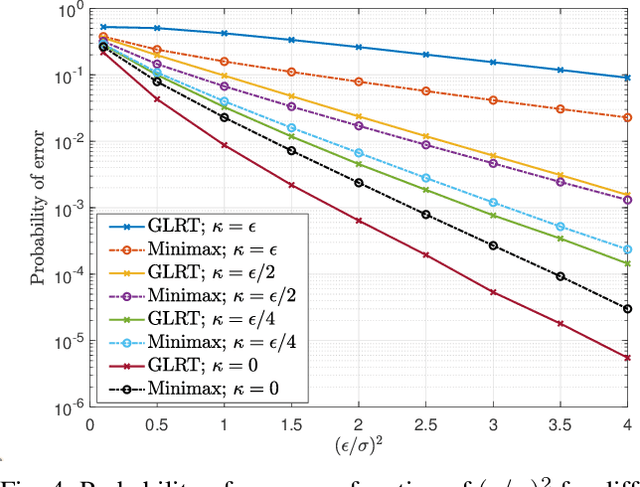
Machine learning models are known to be susceptible to adversarial attacks which can cause misclassification by introducing small but well designed perturbations. In this paper, we consider a classical hypothesis testing problem in order to develop fundamental insight into defending against such adversarial perturbations. We interpret an adversarial perturbation as a nuisance parameter, and propose a defense based on applying the generalized likelihood ratio test (GLRT) to the resulting composite hypothesis testing problem, jointly estimating the class of interest and the adversarial perturbation. While the GLRT approach is applicable to general multi-class hypothesis testing, we first evaluate it for binary hypothesis testing in white Gaussian noise under $\ell_{\infty}$ norm-bounded adversarial perturbations, for which a known minimax defense optimizing for the worst-case attack provides a benchmark. We derive the worst-case attack for the GLRT defense, and show that its asymptotic performance (as the dimension of the data increases) approaches that of the minimax defense. For non-asymptotic regimes, we show via simulations that the GLRT defense is competitive with the minimax approach under the worst-case attack, while yielding a better robustness-accuracy tradeoff under weaker attacks. We also illustrate the GLRT approach for a multi-class hypothesis testing problem, for which a minimax strategy is not known, evaluating its performance under both noise-agnostic and noise-aware adversarial settings, by providing a method to find optimal noise-aware attacks, and heuristics to find noise-agnostic attacks that are close to optimal in the high SNR regime.

Adversarially Robust Classification based on GLRT

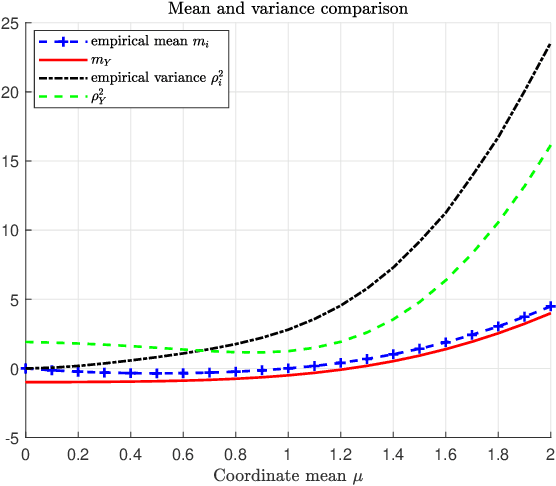
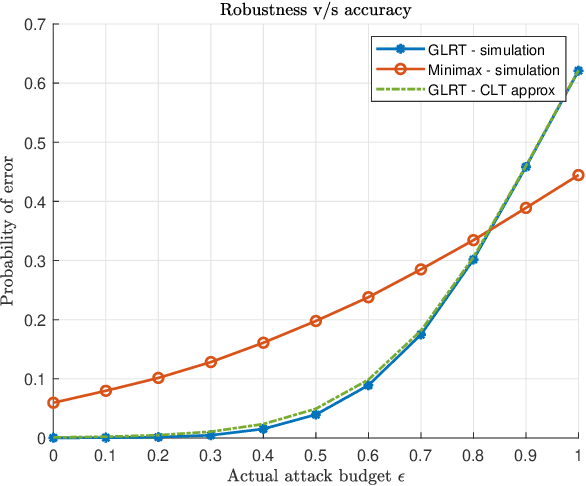
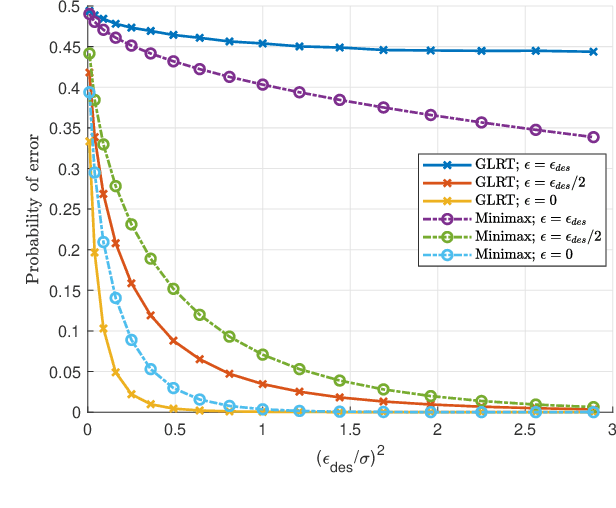
Machine learning models are vulnerable to adversarial attacks that can often cause misclassification by introducing small but well designed perturbations. In this paper, we explore, in the setting of classical composite hypothesis testing, a defense strategy based on the generalized likelihood ratio test (GLRT), which jointly estimates the class of interest and the adversarial perturbation. We evaluate the GLRT approach for the special case of binary hypothesis testing in white Gaussian noise under $\ell_{\infty}$ norm-bounded adversarial perturbations, a setting for which a minimax strategy optimizing for the worst-case attack is known. We show that the GLRT approach yields performance competitive with that of the minimax approach under the worst-case attack, and observe that it yields a better robustness-accuracy trade-off under weaker attacks, depending on the values of signal components relative to the attack budget. We also observe that the GLRT defense generalizes naturally to more complex models for which optimal minimax classifiers are not known.