Adversarially Robust Classification based on GLRT
Paper and Code
Nov 16, 2020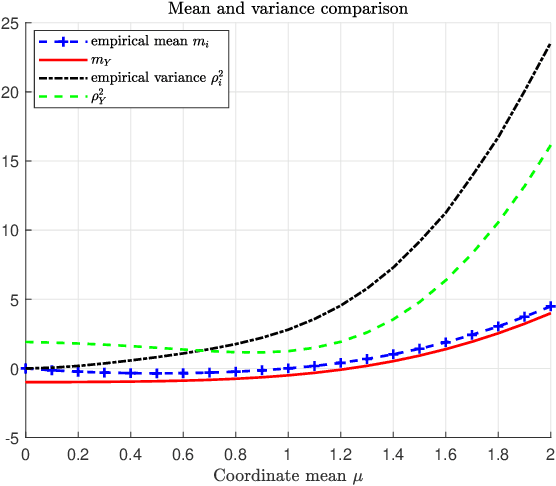
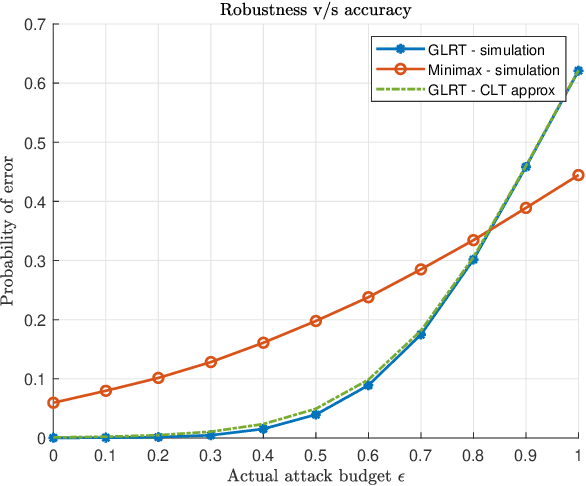
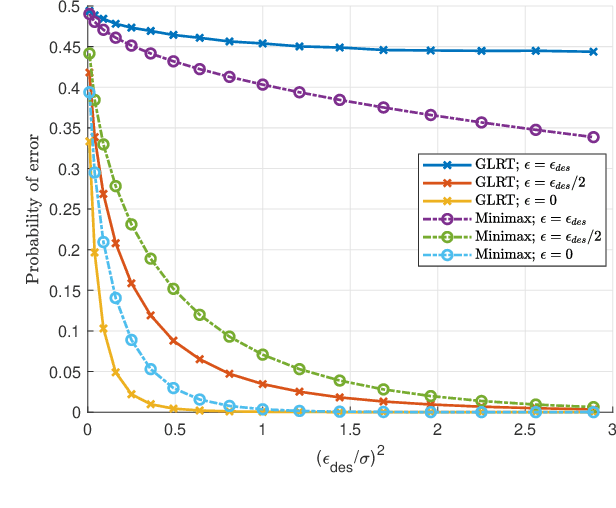
Machine learning models are vulnerable to adversarial attacks that can often cause misclassification by introducing small but well designed perturbations. In this paper, we explore, in the setting of classical composite hypothesis testing, a defense strategy based on the generalized likelihood ratio test (GLRT), which jointly estimates the class of interest and the adversarial perturbation. We evaluate the GLRT approach for the special case of binary hypothesis testing in white Gaussian noise under $\ell_{\infty}$ norm-bounded adversarial perturbations, a setting for which a minimax strategy optimizing for the worst-case attack is known. We show that the GLRT approach yields performance competitive with that of the minimax approach under the worst-case attack, and observe that it yields a better robustness-accuracy trade-off under weaker attacks, depending on the values of signal components relative to the attack budget. We also observe that the GLRT defense generalizes naturally to more complex models for which optimal minimax classifiers are not known.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge